Week 9 No Free Lunch Theorem

字数

2057 字

阅读时间

8 分钟

黑盒优化

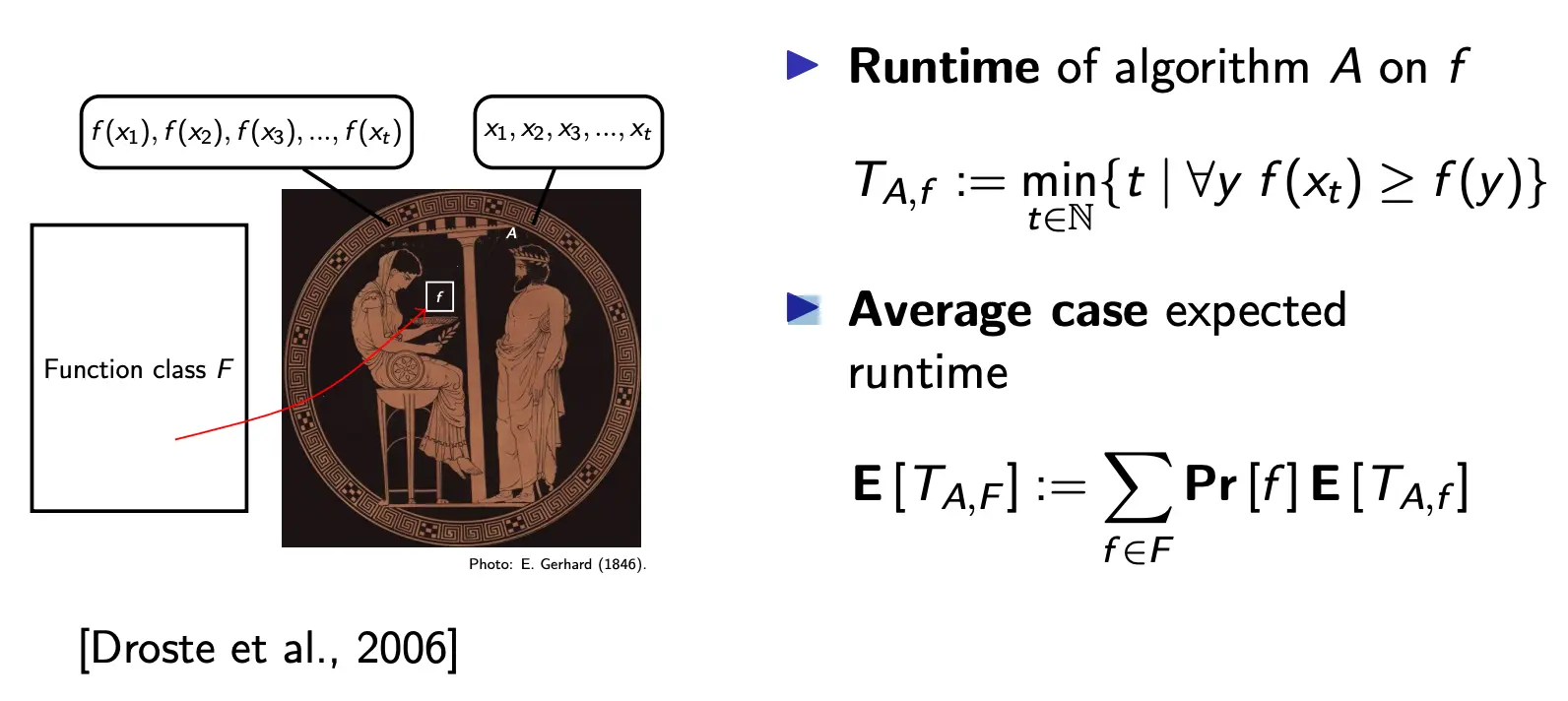这幅图中，F是一个函数集合，里面有一堆f1, f2, f3... 对于每个f，你不知道他的公式是啥，只能不断地试，不断试x1, x2, x3...，对方告你f(x1), f(x2), f(x3) 那么TA,f就定义为，A这个优化算法在f这个函数上，找到最优值的时间。而如何评价一个A在一群函数上的优化效果呢？就用E(TA,F)。这个metric衡量了一个优化算法在一系列函数F中的总体优化能力。

那么黑盒优化算法的流程就如下：首先用一个随机的分布在搜索空间X上取一个起点x0, R0表示已经访问的点，然后计算R0中的fitness。进入循环，首先计算Ht为点与fitness的集合，然后根据这个Ht，根据某种规则得到一个新的分布pt，用这个分布在搜索空间X中去掉已经访问的点的剩余点中采样一个新点xt，把xt加入到已访问的点中，直到停止flag达到。

这个算法框架大概描述了所有优化算法的一个基本思路。

狭义 No Free Lunch Theorem

一句话，如果把优化问题种类无限拓展（被优化函数集是无限的），那么任何两个黑箱优化算法的性能（比如找到最优值的速度）都是一样的。没有哪个算法在所有问题上都更好！另外，任何不接触被优化问题表达式的优化算法都是黑箱优化，比如遗传算法，模拟退火都是。但是，梯度下降就不算，因为你知道了f(x)的表达式。你把优化原问题变成了优化损失函数罢了。

广义NFL定理

原本的NFL的定义有点紧了，要求被优化函数集是无限的。而广义的NFL定理如下：首先定义置换封闭。如何理解置换封闭？functions closed under permutations (c.u.p.) 如果f(x)在函数集F中，那么对于任何的打乱sigma，f(sigma(x))依旧在函数集F中。sigma就是那个箭头顺序。 cup长什么样子呢？长这样：你无论怎么换三个集合体的顺序，都能以另一个f表示出来。这就是对置换封闭。那么广义NFL就定义为：如果F是对置换封闭的，那么任何两个黑箱优化算法A和B，他们在F上的平均性能相同。

注意！

CUP其实隐含着置换后的 $f \circ σ$ 与f的可能性相同。最简单的情况就是给F中所有函数相同的概率。

广义NFL的证明

要证明广义NFL，我们就需要先证明两个idea。

idea 1 缩小范围后依旧满足置换封闭

我们可以看到，原函数集合是满足置换封闭的。当我们限定了f(⭕️) = 1的情况下，之后的函数集合依旧满足置换封闭。我们把这个形式定义为：

F (x, b) := {f \in F ∣ f (x) = b},

这意味着给定x的情况下F中满足f(x)=b的所有函数。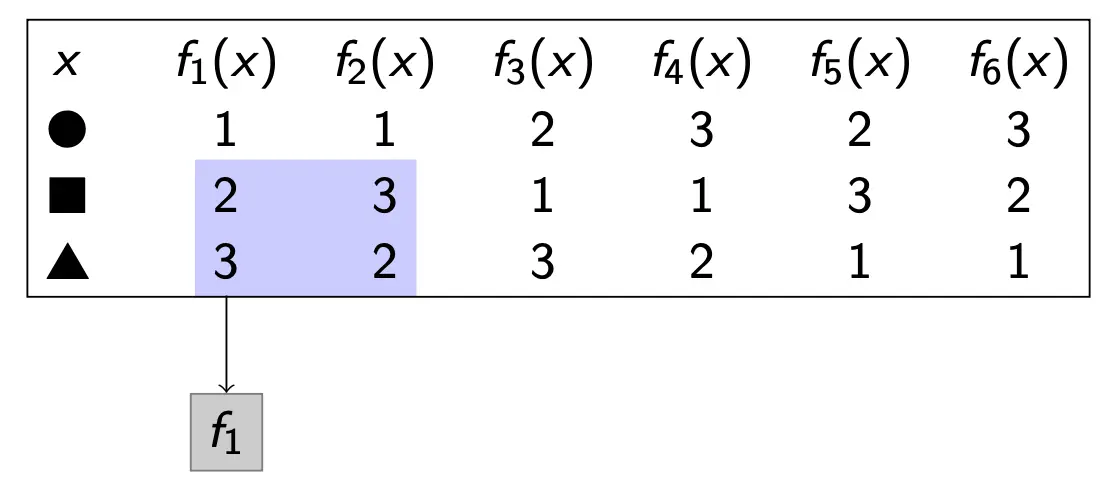

idea 2 不管从什么起点开始都同构 (isomorphism)

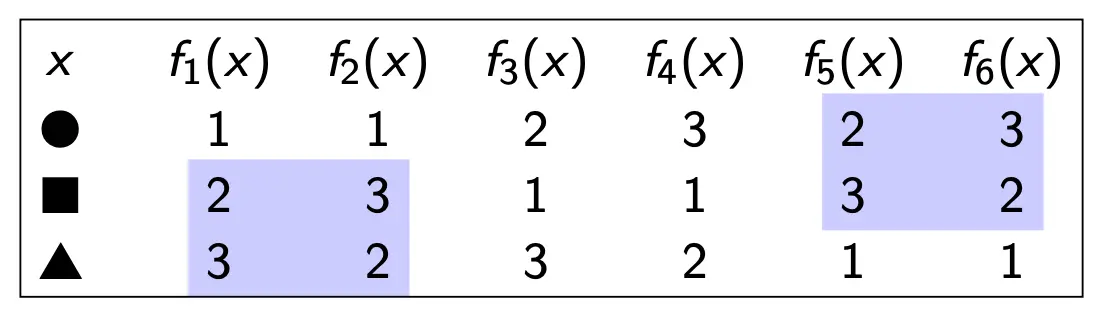可以看到，不管是F(⭕️, 1)还是F(三角, 1)，这两个问题显然同构。所以有： F(x,b)与F(y,b)永远同构。

正式证明

先证明在确定性算法上成立

我们用数学归纳法证明。思路：先证明在搜索空间只有一个点的时候NFL成立，然后证明N个点的时候成立，N+1也成立。

搜索空间只有一个点时成立

我们假设有两个黑箱优化算法A和B，A选择x作为起点，B选择y作为起点，当搜索空间只有一个点的时候，x=y且f(x)一定最优，所以显然成立

假设N成立，推理N+1成立

还是构建两个黑箱优化算法A和B，A选择x作为起点，B选择y作为起点。我们可以写出A和B在搜索空间为N+1个时的期望时间：

\begin{aligned} E [T_{A, F}] = \Pr [f (x) = b^{*}] \cdot 1 + \sum_{b \neq b^{*}} \Pr [f (x) = b] \cdot (1 + E [T_{A, F (x, b)}]) . \\ E [T_{B, F}] = \Pr [f (y) = b^{*}] \cdot 1 + \sum_{b \neq b^{*}} \Pr [f (y) = b] \cdot (1 + E [T_{B, F (y, b)}]) . \end{aligned}

这很好理解，假设A和B做一次搜索的时间都是1，那么期望时间就是fx=bstar的概率乘1，加上fx不等于bstar的概率乘上1+原来的时间。看到ETAF和ETBF的差距只有最后一项ETAF(x,b)和ETBF(y,b) 而根据idea2：F(x,b)与F(y,b)永远同构，且NFL在N时成立，所以这二者相等，所以N+1成立。

再推广到随机算法

一个随机黑箱优化算法A可以被解构为，在“众多确定性算法”之间随机选一个来运行。那本质上一个随机黑箱优化算法A就可以被看成是不同确定性算法Ai的加权平均。那这就太简单了。我们已经证明了不同确定性算法的效能一样，那加权平均也肯定一样，QED。

然而，广义NFL在现实中不怎么适用

广义NFL去表示出一半的函数的存储空间已经爆炸了，所以你在现实生活中几乎碰不到。 NFL定理在数学上成立，但它依赖的前提（比如“所有函数等可能”）在现实中根本不会出现，现实中的问题有结构、有模式、有偏好，算法是可以利用这些的。有模式是最重要的，存储空间也是重要的。

Almost NFL定理

即使一个函数只改动很少部分，也足以让原先的黑箱算法在新函数上几乎必定找不到最优。

经典 NFL 定理需要考虑所有可能的函数都等可能，才能说“没有算法能在平均上更优”。这个定理展示了：即使你不考虑所有函数，只要对一个具体函数 f 稍微改动一点点，就可以让算法原本的优势荡然无存。这些“陷阱函数”的构造并不难，还能有指数级多种选择。

设定函数为f n位比特串 -> N个整数中的一个。那么总共有多少映射呢？ $N^{2^{n}}$ 个。那么定理说，至少存在 $N^{2^{n / 3} - 1}$ 个函数f star, 满足：

与原函数f几乎相同，是有最多 $2^{n / 3}$ 不同, 其他输入与f完全一致。
算法A几乎无法在f star上找到最优，在 $2^{n / 3}$ 步内找到最优的概率小于等于 $2^{- n / 3}$
这些 fstar 并不复杂，很自然。只比原函数f高一个O(n)的小增量。并不是那种“天马行空、无法实现”的怪函数

结论

没有任何单一的搜索启发式能在所有问题上都表现最优。在真实应用里，函数往往拥有一定结构（不满足对置换封闭），所以一些启发式算法能比其他算法更有效。
但若考虑“所有可能函数”或在“对置换封闭”类中，并给每个函数等可能性，则不会有一个算法在平均意义上更优。
“Almost NFL” 进一步表明，即使对一个已知好处理的函数做微小改动，也可以让原本高效的算法彻底失灵。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

Week 9 No Free Lunch Theorem ​

黑盒优化 ​

狭义 No Free Lunch Theorem ​

广义NFL定理 ​

广义NFL的证明 ​

idea 1 缩小范围后依旧满足置换封闭 ​

idea 2 不管从什么起点开始都同构 (isomorphism) ​

正式证明 ​

先证明在确定性算法上成立 ​

搜索空间只有一个点时成立 ​

假设N成立，推理N+1成立 ​

再推广到随机算法 ​

然而，广义NFL在现实中不怎么适用 ​

Almost NFL定理 ​

结论 ​

贡献者 ​

文件历史 ​