Bayesian Regression

字数

1309 字

阅读时间

6 分钟

频率派 vs 贝叶斯派

拿线形回归举例。频率派认为，参数w都是定的，而误差来自于不可学习的噪声epsilon 贝叶斯派认为，参数w都是一个条件概率分布，而误差来自于w分布你选择不同的w。数据量越大，这个分布就越集中。 贝叶斯派：

$$P(\omega \mid y,X)=\frac{P(y\mid X,\omega )P(\omega )}{P(y\mid X)}\to P(\omega \mid y,X)\propto P(y\mid X,\omega )P(\omega )$$

概率视角下的线性回归

我们认为，w是确定的，不确定性来自于噪声epsilon：

$$\mathbf{y}=\hat{y}(\mathbf{x},\mathit{\omega })+ϵ$$

而我们认为噪声epsilon为高斯分布，且记 $\beta =\frac{1}{{\sigma }^2}$ , 那么有：

$$p(y\mid \mathbf{x},\omega ,\beta )=\mathcal{N}(y\mid \hat{y}(\mathbf{x},\omega ),{\beta }^{-1})$$

对于多元正态分布，方差会被换成协方差矩阵 $\mathrm{\Sigma }$ 。由于我们的训练集给出了X和y，那么我们认为这样出现的概率就应当最高。所以我们应当使得P(y|X)最高，加上w不确定的情况下，就变成了我们希望p(y|X, w)最高。似然函数：

$$p(\mathbf{y}\mid \mathbf{X},\mathit{\omega },\beta )=\prod _{i=1}^N\mathcal{N}(y_i\mid {\mathit{\omega }}^T\varphi (x_i),{\beta }^{-1})$$

对数似然：

$$\mathcal{L}=\ln p(\mathbf{y}\mid \mathbf{X},\mathit{\omega },\beta )=-\frac{ND}{2}\ln (2\pi )-\frac{N}{2}\ln \beta -\frac{1}{2}\sum _{i=1}^N\beta (y_i-{\mathit{\omega }}^T\varphi (x_i){)}^2$$

而由于前两项都是定值，所以我们最大化L就相当于要最小化：

$$R(\omega )=\sum _{i=1}^N(y_i-{\omega }^T\varphi (x_i){)}^2=\sum _{i=1}^N(y_i-{\hat{y}}_i(x_i,\omega ){)}^2$$

这就可以看出，在点估计，频率派的视角下来看，OLS和MLE是一样的。

贝叶斯视角下的线性回归

当数据和模型处于一个过定状态的时候，你最后学出的内容可以是一条线，并认为误差是噪声带来的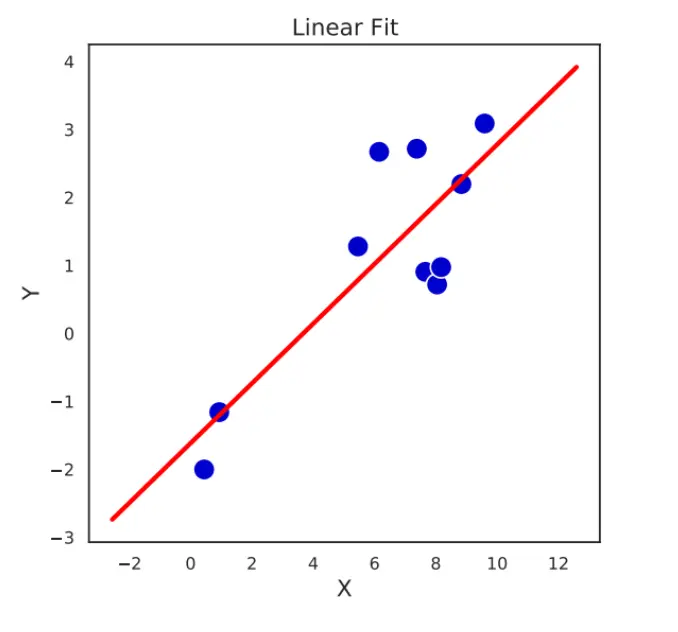： 但当系统欠定的时候，实际上可以有多个线，且每个线的可能性不太一样，这里就需要贝叶斯派，用概率来确定参数的family。 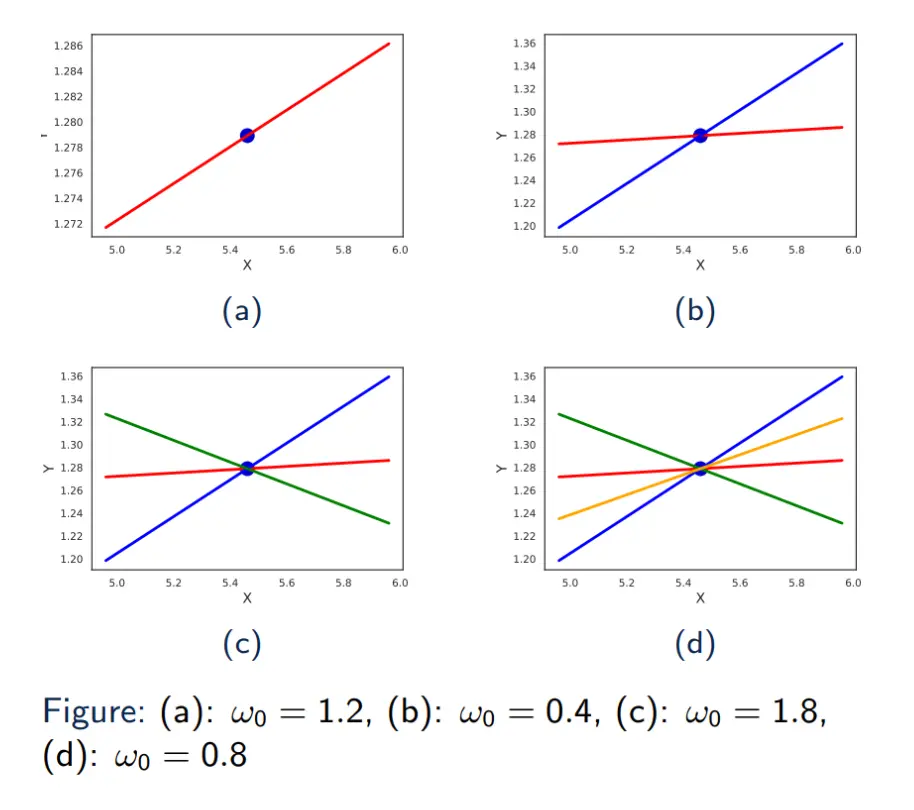在频率视角中，当我们得到似然函数之后，我们做的是最大似然函数。但是在贝叶斯视角中，我们先停在似然函数：

$$p(\mathbf{y}\mid \mathbf{X},\mathit{\omega },\beta )=\prod _{i=1}^N\mathcal{N}(y_i\mid {\mathit{\omega }}^T\varphi (x_i),{\sigma }^2)$$

由于多变量的不确定性太难推导，所以我们这里就只考虑，w0，即截距不确定的情况下的贝叶斯视角。 首先，我们有先验知识，认为w0是服从高斯分布的：

$$p({\omega }_0)\sim \mathcal{N}(0,\alpha )$$

那么似然函数为：

$$P(y\mid X,{\omega }_0,{\omega }_1,{\sigma }^2)=\prod _{i=1}^N\mathcal{N}(y_i\mid {\omega }_1{x}_i+{\omega }_0,{\sigma }^2)$$

根据贝叶斯定理，我们有：

$$P({\omega }_0\mid y,X,{\omega }_1,{\sigma }^2)\propto P(y\mid X,{\omega }_0,{\omega }_1,{\sigma }^2)P({\omega }_0)$$

两边取对数，贝叶斯的分母化为const：

$$\ln p({\omega }_0\mid \mathbf{y},\mathbf{x},{\omega }_1,{\sigma }^2)=\{-\frac{1}{2{\sigma }^2}\sum _{i=1}^N(y_i-{\omega }_1{x}_i-{\omega }_0{)}^2-\frac{{\omega }_0^2}{2\alpha }\}+const$$

通过一个复杂的配方过程，我们可以把上面这个结果凑成下面的形式：

$$\ln p({\omega }_0\mid \mathbf{y},\mathbf{x},{\omega }_1,{\sigma }^2)=-\frac{1}{{\sigma }_{post}^2}({\omega }_0-{\mu }_{post}{)}^2+const$$$$p({\omega }_0\mid \mathbf{y},\mathbf{x},{\omega }_1,{\sigma }^2)\sim \mathcal{N}({\mu }_{post},{\sigma }_{post}^2)$$$${\mu }_{post}=\frac{N\alpha }{N\alpha +{\sigma }^2}{\mu }_{ML},{\sigma }_{post}^2=\frac{{\sigma }^2\alpha }{N\alpha +{\sigma }^2}$$

其中 ${\mu }_{ML}$ 是omega在MLE的情况下的截距omega_0 这个形式揭示了，后验分布依旧是一个高斯分布。如果不想只在w0上用不确定性，而是想要推广到所有的w都想要不确定性，那么： 先给出w的先验是高斯分布：

$$P(\omega )=\mathcal{N}(\omega \mid 0,{\alpha }^{-1}I)$$

利用先验和似然，得出w的后验分布：

$$P(\omega \mid y,X)\propto P(y\mid X,\omega )P(\omega )$$$$\ln p(\mathit{w}\mid \mathbf{y},\mathbf{x})=-\frac{\beta }{2}\sum _{i=1}^N{\{y_i-{\mathit{w}}^T\varphi (x_i)\}}^2-\frac{\alpha }{2}{\mathit{w}}^T\mathit{w}+\mathrm{const}$$

配方之后，得到后验依旧是高斯分布：

$$p(\omega \mid \mathbf{y},\mathbf{x})=\mathcal{N}(\omega \mid {\mathbf{m}}_{post},{\mathbf{S}}_{post})$$$${\mathbf{m}}_{post}=\beta {\mathbf{S}}_{post}{\mathbf{\Phi }}^T\mathbf{y},{\mathbf{S}}_{post}^{-1}=\alpha \mathbb{I}+\beta {\mathbf{\Phi }}^T\mathbf{\Phi }$$

其中，$\mathrm{\Phi }$ 是design matrix，上一节讲过。 随着观测数据 N 的增加，后验分布变得越来越集中。这说明参数的不确定性下降，数据越多时，似然函数对后验分布的影响逐渐占主导，后验分布更依赖于观测数据。

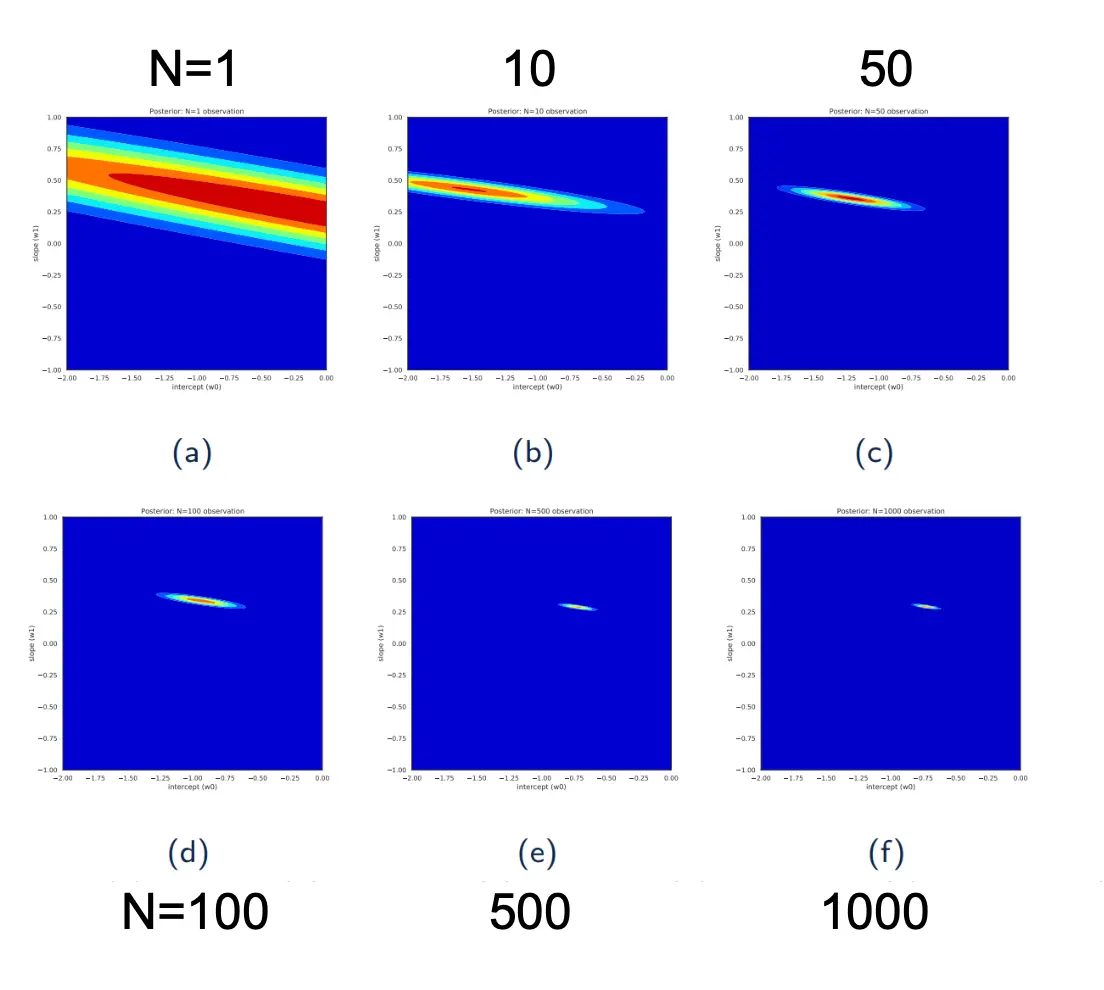
贝叶斯流派估计新数据

预测分布由此公式算出：

$$P(y_{\ast }\mid x_{\ast },X,y)=\int P(y_{\ast }\mid x_{\ast },\omega )P(\omega \mid X,y)d\omega$$

其中，右侧的后半部分已经有了，前半部分呢？对于训练集我们有：

$$P(y_i\mid x_i,\omega )=\mathcal{N}(y_i\mid {\omega }^{\mathrm{\top }}\varphi (x_i),{\beta }^{-1})$$

而由于我们认为，测试集和训练集的采集方法是一样的，即分布是一样的，所以y* 同样满足：

$$P(y_{\ast }\mid x_{\ast },\omega )=\mathcal{N}(y_{\ast }\mid {\omega }^{\mathrm{\top }}\varphi (x_{\ast }),{\beta }^{-1})$$

贝叶斯例子

1. 模型假设
   我们假设观测满足 y=w x+ϵ,ϵ∼N(0,1)

2. 先验
   在看数据前，认为参数 w 服从平均值 0、方差 1 的正态分布：
     w∼N(0,1)

3. 观测数据
   只有两对点：(x,y)=(0,0)，(1,1)。

4. 更新后验

   • 后验的均值就是把数据“加权平均”后得到的最佳估计：$${\mu }_N=\frac{\sum x_i{y}_i}{1+\sum x_i^2}=\frac{0\cdot 0+1\cdot 1}{1+(0^2+1^2)}=\frac{1}{2}.$$
   • 后验的方差表示我们对 ww 的不确定性：
   $${\sigma }_N^2=\frac{1}{1+\sum x_i^2}=\frac{1}{1+1}=\frac{1}{2}.$$

   所以更新后 w 约等于 0.5±\sqrt{0.5}。

5. 做新点预测
   想知道在 x∗=2时，y∗会怎样。贝叶斯预测给我们：

   • 预测均值： $$E[y^]=x^\mu_N=2\times0.5=1。$$
   • 预测方差：模型噪声 1 加上参数不确定带来的额外方差：

$$1+(2^2)\times 0.5=3。$$

因此 y∗ 的分布是 N(1, 3)

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update