GAN
Generative Model 引子
首先,前面讲的VAE 7 - AE VAE, 今天的GAN以及后面的 9 - Diffusion 都属于生成模型。 首先,我们要知道,对于一个有意义的图来说,两个像素之间是有着关系的,如下图。横轴表示了红色像素的亮度,纵轴表示了蓝色像素的亮度,这些点就是亮度组合,可以看出,对于数字这种有意义的图来说,p1和p2的亮度经常是基本相等。而对于噪声来说,两个像素的亮度似乎没什么联系。 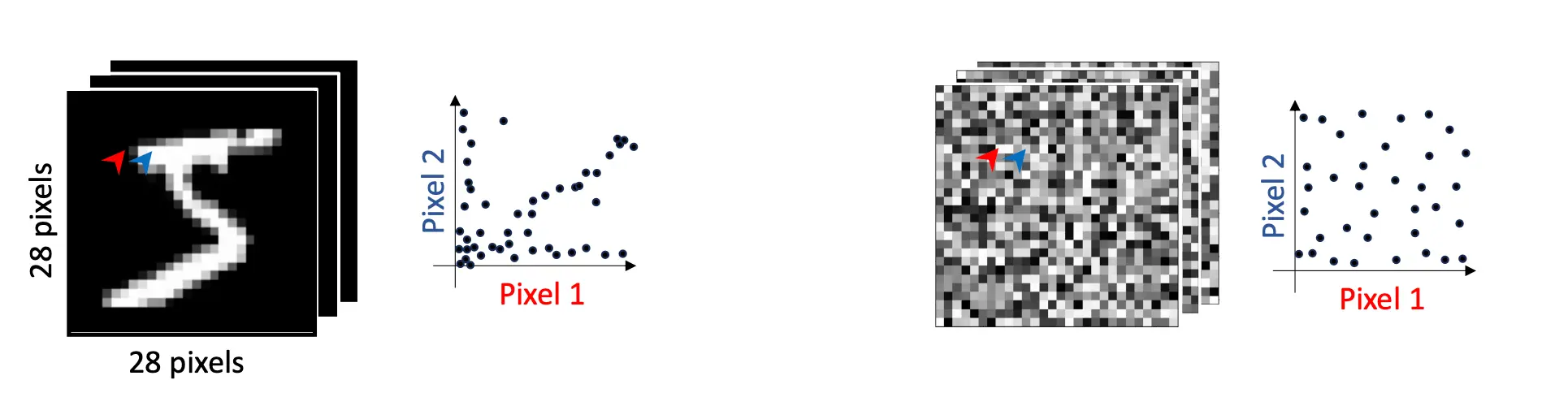
如果我们把28*28的像素图拉开,用亮度去聚合像素的话,那么结果是这样的: 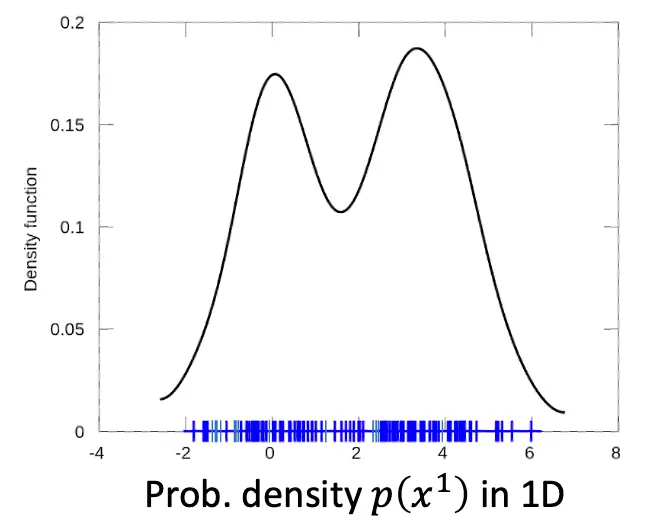 可以看到,对于有意义的图来说,横轴代表着亮度,那么亮度并不是均匀分布的,而是亮度为0和亮度为4的像素点居多。 若是二维概率分布的话,可以看到,p1的亮度在数字上处于-1到1居多,还有2,而p2的亮度在0和1居多,且有群聚效应。
可以看到,对于有意义的图来说,横轴代表着亮度,那么亮度并不是均匀分布的,而是亮度为0和亮度为4的像素点居多。 若是二维概率分布的话,可以看到,p1的亮度在数字上处于-1到1居多,还有2,而p2的亮度在0和1居多,且有群聚效应。 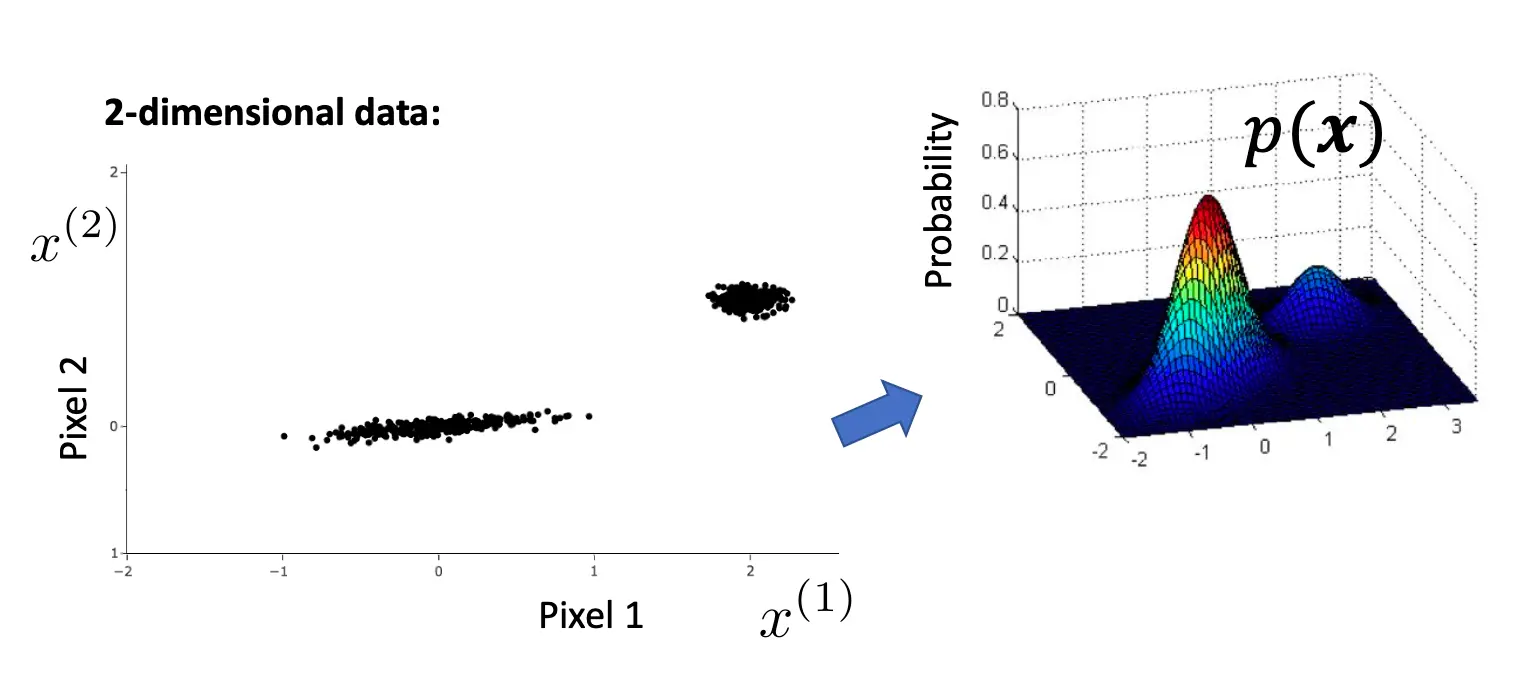 这就说明了,对于有意义的图来说,p(x1,x2..xn) != p(x1) * p(x2) *.....* p(xn), 因为每个像素的亮度分布并不是独立的。而对于噪声来说,基本是独立的。
这就说明了,对于有意义的图来说,p(x1,x2..xn) != p(x1) * p(x2) *.....* p(xn), 因为每个像素的亮度分布并不是独立的。而对于噪声来说,基本是独立的。  而什么是生成模型呢?生成模型就是:
而什么是生成模型呢?生成模型就是:  我们尝试去用神经网络去近似学习一个ptheta去趋近于pdata. 要注意,pdata(x)只反应了概率的高低,并没有反应类别。比如说,x是28*28的一张手写2的照片,输入进去,根据每个像素的亮度,如果这个手写2很清晰很容易辨别,那么pdata(x)就会很高,但如果很模糊,就会低。但是,并不是说只有2才会高。如果你输如的是清晰的3,4,那么也会高。所以仅依靠pdata(x)是无法分类的。 如果想要分类,你需要这种分布:pdata(x, y)。
我们尝试去用神经网络去近似学习一个ptheta去趋近于pdata. 要注意,pdata(x)只反应了概率的高低,并没有反应类别。比如说,x是28*28的一张手写2的照片,输入进去,根据每个像素的亮度,如果这个手写2很清晰很容易辨别,那么pdata(x)就会很高,但如果很模糊,就会低。但是,并不是说只有2才会高。如果你输如的是清晰的3,4,那么也会高。所以仅依靠pdata(x)是无法分类的。 如果想要分类,你需要这种分布:pdata(x, y)。
GAN介绍
GAN总体上是通过采样分布来生成,和VAE的原理差不多 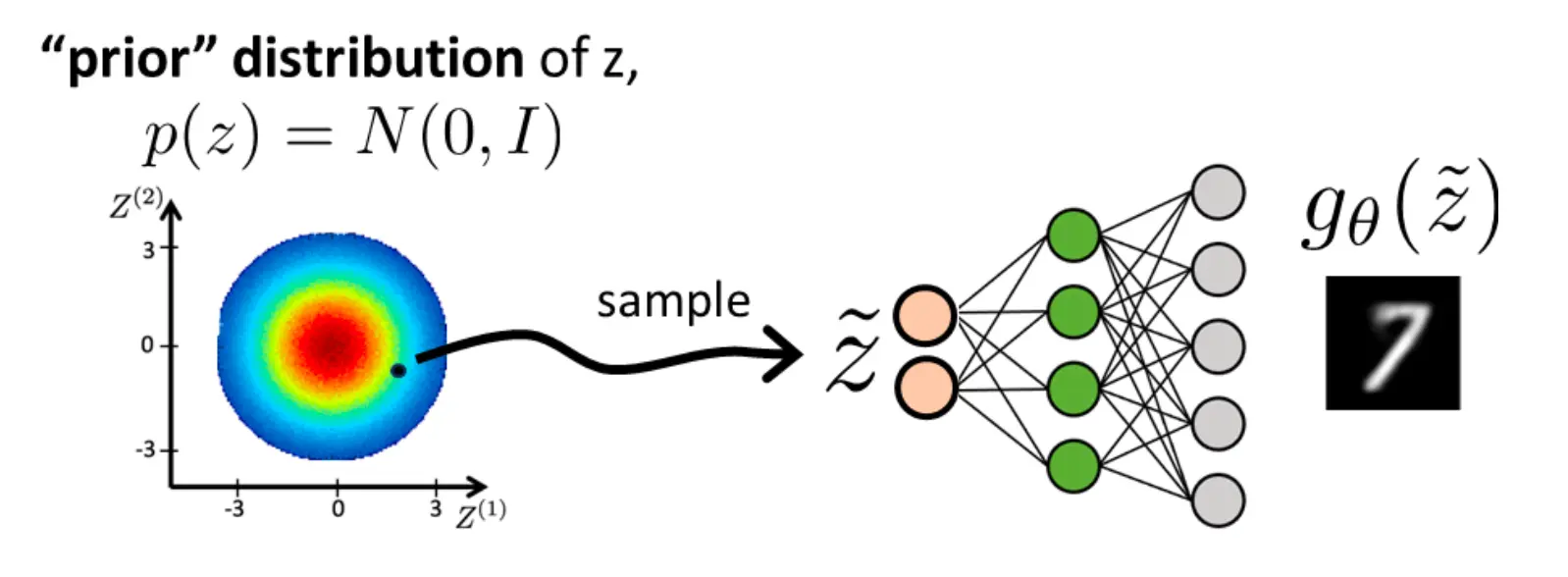 然而,GAN的训练是采用了这样的架构的:
然而,GAN的训练是采用了这样的架构的: 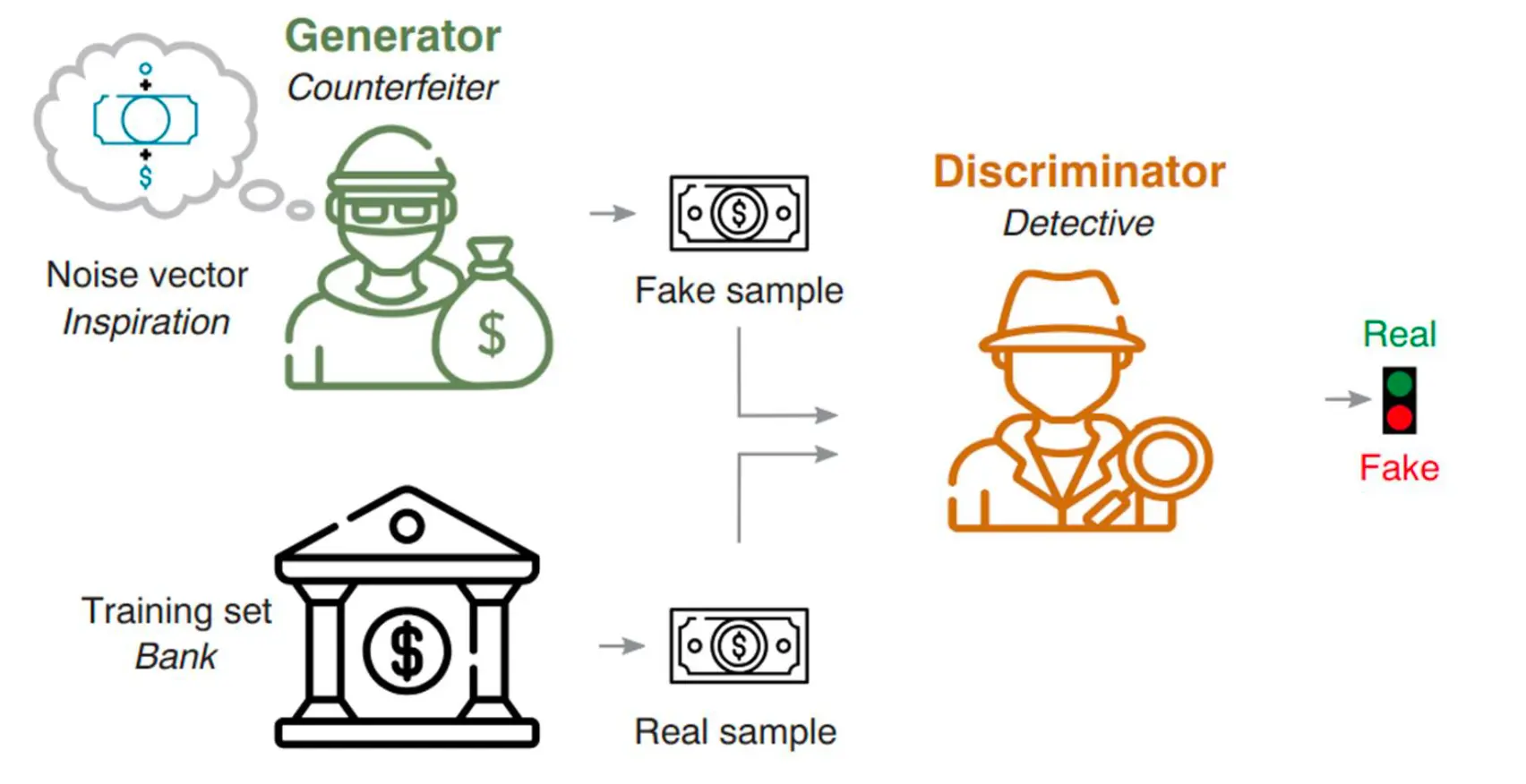 反映到架构上,就是长这样:
反映到架构上,就是长这样:
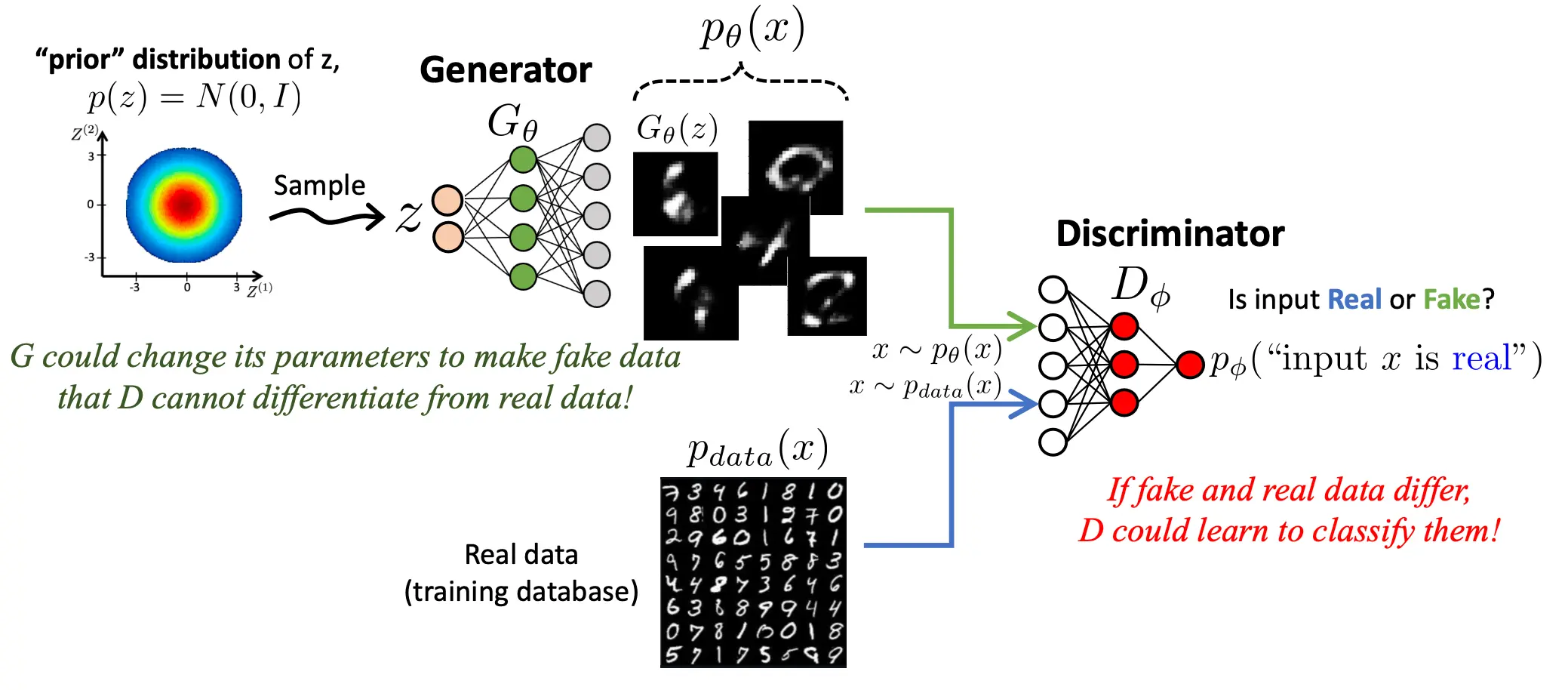
而损失函数是这样设计的:
这其实很好理解。我们要取theta,使得loss最小(差距最小),这是对的,因为theta是生成器的参数,我们要让生成器生成最真的图。但是同时,我们还要取让loss最大的phi,因为phi是分辨器的参数,我们希望D能够在数据是真的时候输出1,数据是生成的时候输出0。
在理论中怎么训练呢?  先训练K个循环的分辨器,再训练生成器。在训练一方的时候,另一方的参数是固定的。
先训练K个循环的分辨器,再训练生成器。在训练一方的时候,另一方的参数是固定的。
然而,在实践中,我们在优化theta的时候采用这样的形式,这虽然修改了函数,但是收敛方向都是一样的。 
为什么GAN有效?因为有人证明了,当分辨器容量无限大的时候,其形式为:
它的意义是:给定样本 xx,它来自真实数据分布 pdata(x)pdata(x) 的概率。具体来说:
- 如果 pdata(x)≫pθ(x)(即 xx 更可能来自真实数据分布),则 Dϕ∗(x)≈1
- 如果 pθ(x)≫pdata(x)(即 xx 更可能来自生成数据分布),则 Dϕ∗(x)≈0 那么代入之后,GAN的损失函数就变成了:
继续推导就变成了
也就是JS散度。由于D已经最优了,所以最大化phi就不存在了,只存在最小化theta使得J变小了,而JS散度变小,就说明想让Pdata和Ptheta一样,也就是说,想让生成分布和真实分布一样。
Conditional Generative Models
你可以通过贝叶斯公式,来这样: 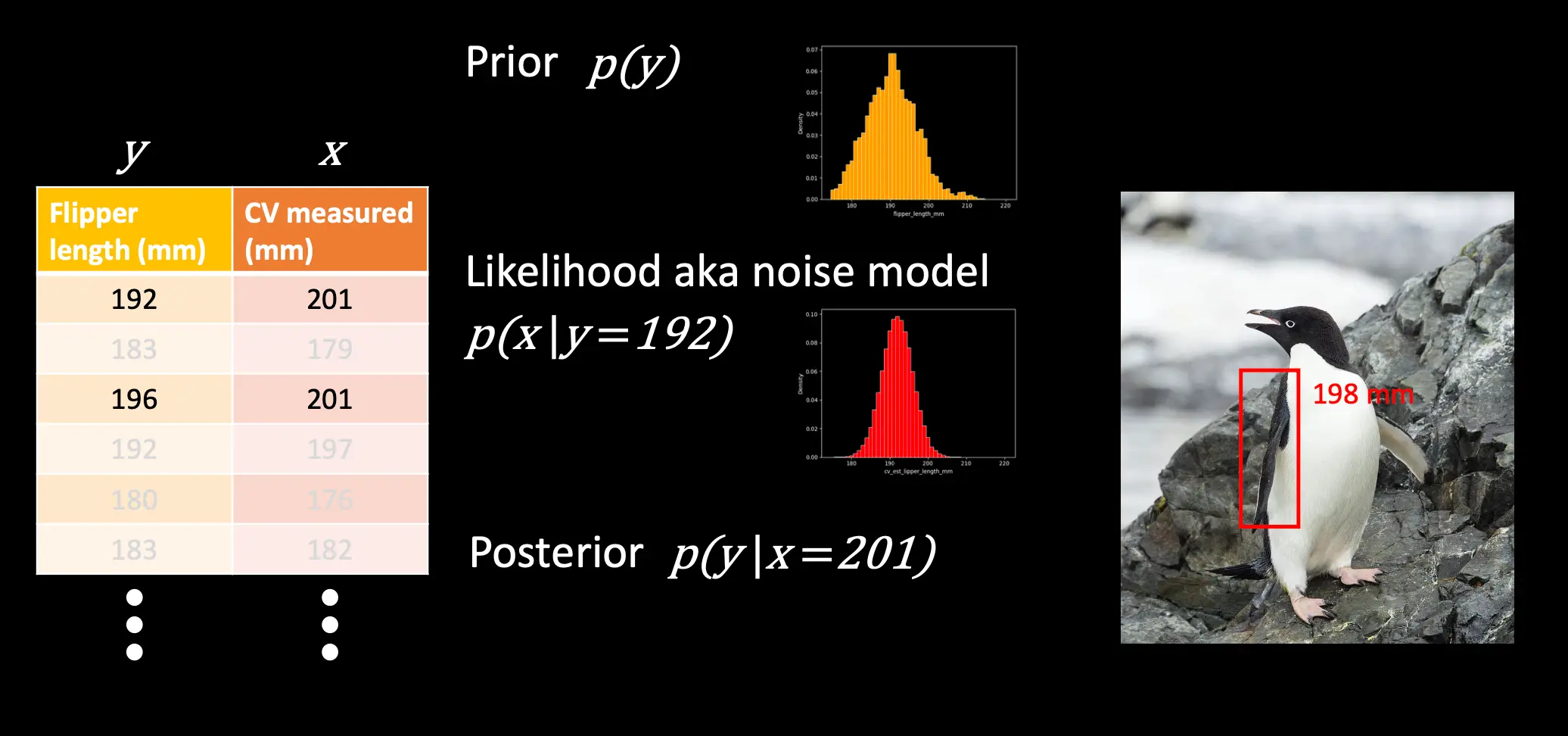
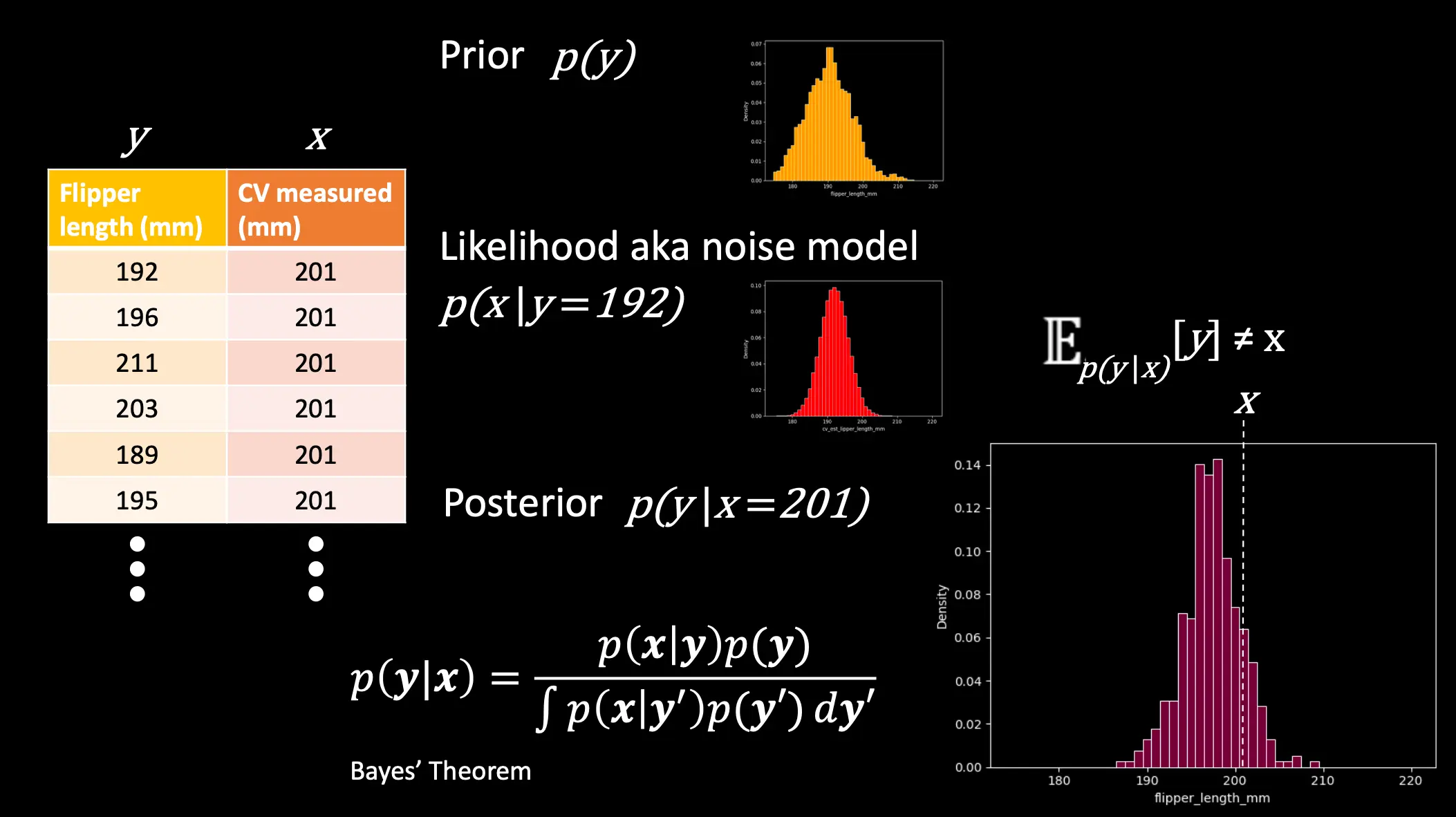
也就是,你可以通过真实分布(先验),以及似然,去得到后验分布。
比如说,超分:  上色:
上色:  还原:
还原: 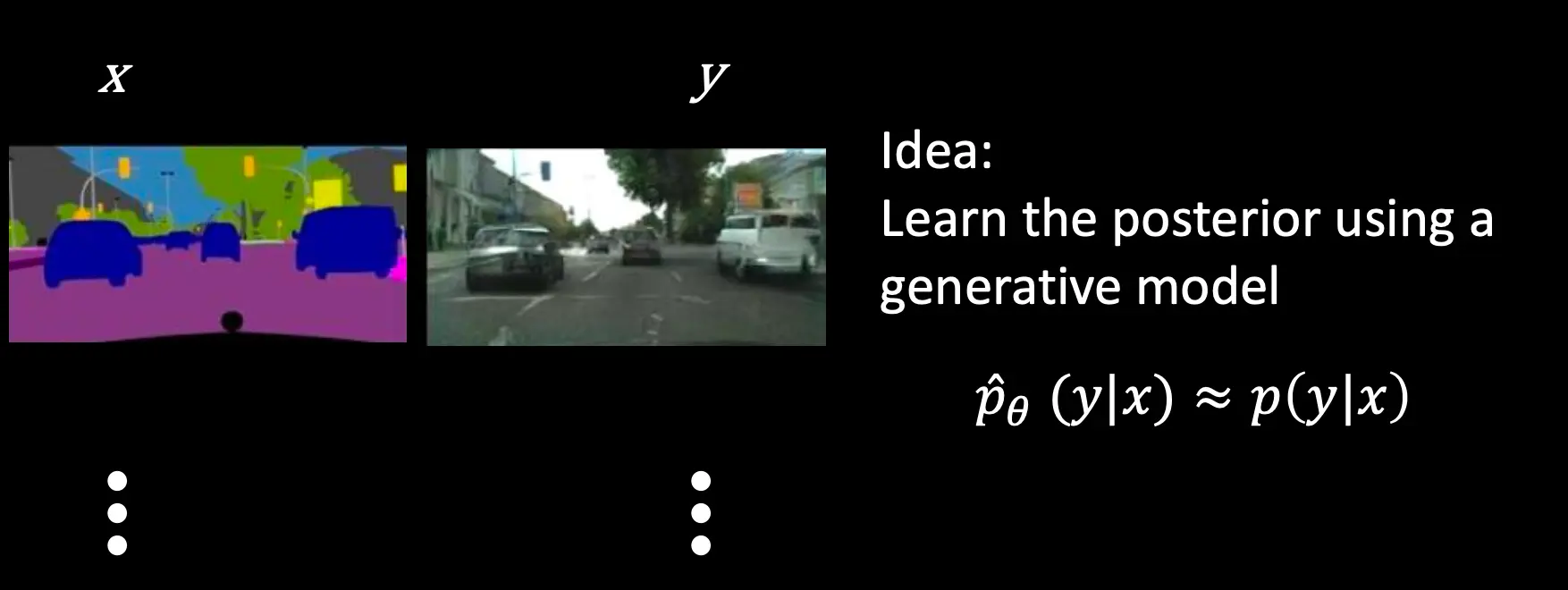 补全:
补全:  修复:
修复: 
 Larry Shi
Larry Shi