Validation

字数

2339 字

阅读时间

10 分钟

Validation: Checking the bottom line 给定M个模型假设空间 ${\mathcal{H}}_1,\dots ,{\mathcal{H}}_M$，每个模型假设空间给定了对应的算法：$A_1,\dots ,A_M$

• 目标：选出最优的 ${\mathcal{H}}_{m^{\ast }}$ ，并希望他在新样本上的期望泛化误差 $E_{\mathrm{out}}(g_{m^{\ast }})$ 尽可能低。
• 挑战：Eout 无法直接计算，因为你没有真实的数据。 模型选择：在候选的Hm中，用某种策略（交叉验证、信息准则、贝叶斯证据等）去估计各自的泛化误差，然后 pick 那个最有希望在“真实环境”里表现最好的m*。

我们有几种方法来做模型选择

• 根据Ein选：这是最容易过拟合的方法，几乎更复杂的模型永远会得到更好的结果
• Etest选择。如果有测试集的话，就对每个候选算法Am在D上训练处gm，在Dtest上算出Etest，选Etest最小的那个模型
  • 根据有限样本版 Hoeffding+并 union bound，对这M个候选假设同时推界，都能保证（以高概率）$$E_{\mathrm{out}}(g_{m^{\ast }})\le E_{\mathrm{test}}(g_{m^{\ast }})+O\left(\sqrt{\frac{\log M}{N_{\mathrm{test}}}}\right).$$
  • 但是哪里来的全新测试集？一旦把它当做模型选择就算作弊。任何后来用它报告的测试误差，都已经被“调过”模型，对它过拟合了一次。

实战做法 - Validation Set

如何划分？ 随机划分。训练集N-K，验证集K。在训练集上跑学习算法，得到假设g-，在Dval上验证误差：

$$E_{\mathrm{val}}(g^{-})=\frac{1}{K}\sum _{(x,y)\in {\mathcal{D}}_{\mathrm{val}}}e(g^{-}(x),y).$$

这里面对于分类任务，就是01误差，对于回归任务，就是平方误差 如果K取得太大，剩下的训练样本就太少，g-本身就会很差。如果K太小，验证误差的方差就会上升、评估不稳定。 一般取数据的20% 作为验证集。

如果用全量D训练，会得到最终模型g，如果只用子集Dtrain训练，就得到g-。他只是用来验证误差的模型，不是最后产品。 我们需要让Eval和Eout关联起来，只有当我们能保证这K个样本和未来要碰到的测试点是同分布独立采样的，Eval才能成为对真实Eout的无偏估计。

接下来，我们要对Eval进行均值和方差的分析。分析均值是为了研究，它是不是无偏地接近Eout。研究方差是为了明确，它的波动有多大？需要多大的K才能使估计稳定可靠。

均值分析

我们想要证明，验证误差：

$$E_{\mathrm{val}}(g^{-})=\frac{1}{K}\sum _{(x,y)\in {\mathcal{D}}_{\mathrm{val}}}e(g^{-}(x),y).$$

是对真实泛化误差：

$$E_{\mathrm{out}}(g^{-})={\mathbb{E}}_{x\sim p(x)}\left[e(g^{-}(x),f(x))\right]$$

的无偏估计，也就是证明：

$${\mathbb{E}}_{{\mathcal{D}}_{\mathrm{val}}}[E_{\mathrm{val}}(g^{-})]=E_{\mathrm{out}}(g^{-}).$$

在所有可能的Dval上的平均值。

我们来算左边：

$${\mathbb{E}}_{{\mathcal{D}}_{\mathrm{val}}}[E_{\mathrm{val}}(g^{-})]={\mathbb{E}}_{{\mathcal{D}}_{\mathrm{val}}}[\frac{1}{K}\sum _{{\mathit{x}}_n\in {\mathcal{D}}_{\mathrm{val}}}\mathrm{e}(g^{-}({\mathit{x}}_n),y_n)]$$

因为线性，所以EDval可以进去：

$$=\frac{1}{K}\sum _{{\mathit{x}}_n\in {\mathcal{D}}_{\mathrm{val}}}{\mathbb{E}}_{{\mathcal{D}}_{\mathrm{val}}}[\mathrm{e}(g^{-}({\mathit{x}}_n),y_n)]$$

而由于Dval是独立同分布抽取的，所以Dval单点的分布就是真实分布：

$${\mathbb{E}}_{{\mathrm{D}}_{\mathrm{val}}}\left[\begin{array}{c}e(g^{-}(x_n),y_n)\end{array}\right]={\mathbb{E}}_{x_n\sim p(x)}\left[\begin{array}{c}e(g^{-}(x_n),f(x_n))\end{array}\right]=E_{\mathrm{out}}(g^{-}).$$

方差分析

我们想要知道方差随着K大小的变化的趋势。

$${\sigma }_{\mathrm{val}}^2={\mathrm{Var}}_{{\mathcal{D}}_{\mathrm{val}}}[E_{\mathrm{val}}(g^{-})]={\mathrm{Var}}_{{\mathcal{D}}_{\mathrm{val}}}\left[\frac{1}{K}\sum _{(x_n,y_n)\in {\mathcal{D}}_{\mathrm{val}}}e(g^{-}(x_n),y_n)\right].$$

1/K可以提出来：

$$=\frac{1}{K^2}\sum _{{\mathit{x}}_n\in {\mathcal{D}}_{\mathrm{val}}}\underset{\stackrel{\mathrm{def}}{=}{\sigma }^2(g^{-})}{\underbrace{{\mathrm{Var}}_{{\mathcal{D}}_{\mathrm{val}}}[\mathrm{e}(g^{-}({\mathit{x}}_n),y_n)]}}$$$${\sigma }_{\mathrm{val}}^2=\frac{1}{K^2}\sum _{n=1}^K{\sigma }^2(g^{-})=\frac{1}{K}{\sigma }^2(g^{-}).$$

所以结论为：

$$\boxed{{\displaystyle {\sigma }_{\mathrm{val}}^2=\frac{{\sigma }^2(g^{-})}{K}.}}$$

验证误差的方差随着验证集大小K增加而线性下降。

我们考虑在二分类问题使用01loss，那么我们有：

$${\sigma }_{\mathrm{val}}^2=\mathrm{Var}[\frac{1}{K}\sum _{n=1}^{K}e(g^{-}(x_n),y_n)]=\frac{1}{K^2}\sum _{n=1}^K\mathrm{Var}[e(g^{-}(x_n),y_n)]=\frac{1}{K}\mathrm{Var}\left[e(g^{-}(x),y)\right].$$

而由于二分类问题的Var(e)是一个伯努利随机变量，所以其方差是p(1-p)，因此

$${\sigma }_{\mathrm{val}}^2=\begin{array}{c}\frac{1}{K}p(1-p)\end{array}\le \begin{array}{c}\frac{1}{K}\cdot \frac{1}{4}=\end{array}\frac{1}{4K},$$

所以结论为：当K趋向无穷时，验证误差的随机波动可以通过增大验证集规模任意地控制到很小。

是否泛化

验证误差是否能很好的泛化到Eout呢？

• 均值：无偏估计。验证误差的期望正好等于模型的真实泛化误差，是一个无偏估计。
• 方差：O(1/K)。$${\sigma }_{\mathrm{val}}^2=\mathrm{Var}[\frac{1}{K}\sum _{n=1}^{K}e(g^{-}(x_n),y_n)]=\frac{1}{K^2}\sum _{n=1}^K\mathrm{Var}[e(g^{-}(x_n),y_n)]=\frac{1}{K}\mathrm{Var}[e(g^{-}(x),y)]=O\left(\frac{1}{K}\right).$$
• Hoeffding 不等式的应用
  • 因为Eval(g-)是K个Bernoulli 变量的平均，由 Hoeffding 不等式可推出：$$E_{\mathrm{out}}(g^{-})\le E_{\mathrm{val}}(g^{-})+O\left(\frac{1}{\sqrt{K}}\right).\$\$\mathrm{也}\mathrm{就}\mathrm{是}\mathrm{说}，\mathrm{只}\mathrm{要}\mathrm{验}\mathrm{证}\mathrm{集}\mathrm{足}\mathrm{够}\mathrm{大}，\mathrm{验}\mathrm{证}\mathrm{误}\mathrm{差}\mathrm{不}\mathrm{仅}\mathrm{无}\mathrm{偏}，\mathrm{而}\mathrm{且}\mathrm{波}\mathrm{动}\mathrm{很}\mathrm{小}，\mathrm{能}\mathrm{够}\mathrm{以}\$O(1/\sqrt{K})\$\mathrm{的}\mathrm{速}\mathrm{度}\mathrm{收}\mathrm{敛}\mathrm{到}\mathrm{泛}\mathrm{化}\mathrm{误}\mathrm{差}。$$
  $$E_{\mathrm{out}}(h)\le E_{\mathrm{in}}(h)+O\left(\frac{1}{\sqrt{N}}\right),\$\$N\mathrm{是}\mathrm{训}\mathrm{练}\mathrm{集}\mathrm{大}\mathrm{小}，\mathrm{而}\ast \ast \mathrm{验}\mathrm{证}\mathrm{误}\mathrm{差}\ast \ast \mathrm{的}Hoeffding\mathrm{保}\mathrm{证}\mathrm{只}\mathrm{依}\mathrm{赖}\mathrm{于}\mathrm{验}\mathrm{证}\mathrm{集}\mathrm{大}\mathrm{小}K，$$
• 验证误差的期望正好是该模型的真实错误（无偏）。
• 验证误差的标准误差为 $O(1/\sqrt{K})$ ，可以任意小
• 因此，验证集方法既可行又可靠，是我们在实践中进行模型选择和超参数调优的根基。

大K还是小K

验证集越大，对验证误差的估计越稳定（波动小），这看起来“越好”。 但如果K极大，那么训练用数据就只有N-K，导致g-本身的泛化能力变差。验证误差的期望会上升 如果把K取得很小，模型本身不错，但验证集太小，估计方差大，验证误差很不稳定。 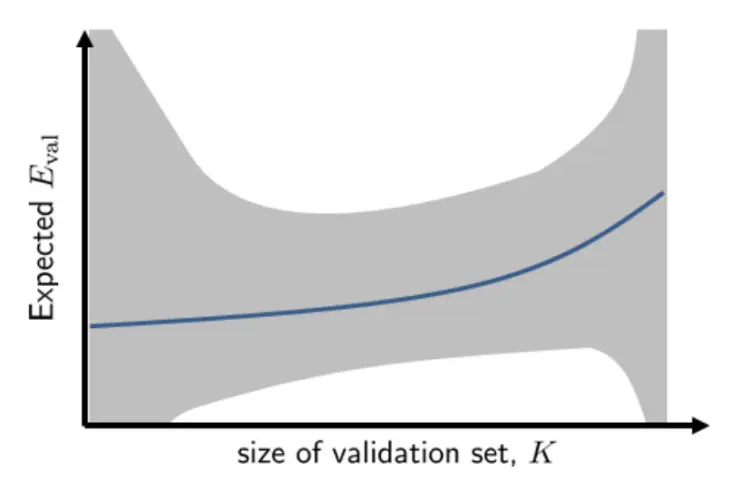灰带是验证误差波动，蓝带是bias。左端K小验证误差波动（灰带）非常大。右端K大，虽然灰带（方差）收窄，但曲线的期望（Bias）向上抬，说明模型因训练数据不足而性能下降。

典型的经验法则是把约五分之一作为验证集。如果特别在意方差，可以用交叉验证（cross-validation）把验证过程重复多次，再平均结果，从而在不牺牲训练数据规模的前提下，进一步降低估计的方差。

基于Validation来选模型

• 准备M个不同模型：$$\mathcal{H}_1,\mathcal{H}_2,\ldots,\mathcal{H}_M.$$
• 训练各个“子模型”，将原始数据集D随机划分为训练集Dtrain和验证集Dval。对每个候选模型Hm在训练集上运行学习算法Am得到一个临时模型：$$g_m^-=\mathcal{A}m\left(\mathcal{D}{\mathrm{train}}\right),\quad m=1,\ldots,M.$$
• 在验证集上评估每个临时模型的平均误差：$$E_m\mathrm{~=~}E_{\mathrm{val}}{\left(g_m^-\right)}\mathrm{~=~}\frac{1}{K}\sum_{(x,y)\in\mathcal{D}_{\mathrm{val}}}e{\left(g_m^-(x),y\right)}.$$
• 选择最优模型。取验证误差最低的一号：$$m^*=\arg\min_{1\leq m\leq M}E_m.$$
• 一旦选定了m*，可以用全量数据集D重新训练一遍，得到最终模型。 显然，我们有：

$$\underset{\text{最终模型的泛化误差}}{\underbrace{E_{\mathrm{out}}(g_{m^{\ast }})}}\le \underset{\text{临时模型的泛化误差}}{\underbrace{E_{\mathrm{out}}(g_{m^{\ast }}^{-})}}\le \underset{\text{最小验证误差}}{\underbrace{E_{\mathrm{val}}(g_{m^{\ast }}^{-})}}+O\left(\sqrt{\frac{\ln M}{K}}\right).$$

Cross Validation

Leave-one-out Cross Validation

原始数据集N个点：

$$\mathcal{D}=\{(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)\}.$$

把第 n个样本剔除，剩下：$$\mathcal{D}_n=\mathcal{D}\setminus{(x_n,y_n)}.$$ 在剔除后的训练集上训练：

$$g_n^{-}=\mathcal{A}({\mathcal{D}}_n).$$

计算这个模型在被剔除的点上的验证误差：

$$e_n=E_{\mathrm{val}}\left(g_n^{-}\right)=\ell (g_n^{-}(x_n),y_n),$$

重复N次，得到：$$ e_1,e_2,\ldots,e_N$$ 最终的估计是所有e的平均：

$$E_{\mathrm{cv}}=\frac{1}{N}\sum _{n=1}^N{e}_n.$$

优点：

• 用尽了几乎所有数据做训练，避免了“训练样本太少”的欠拟合风险；
• 对泛化误差的估计更稳定、无偏。 缺点：
• 需要训练 N次，计算量通常会很大。
  • 在带L2正则的岭回归场景，Ecv有快速计算公式。岭回归有解析解：$$w^{\ast }(\lambda )={(A^{\mathrm{\top }}A+\lambda I)}^{-1}{A}^{\mathrm{\top }}y,\$\$\mathrm{我}\mathrm{们}\mathrm{定}\mathrm{义}\mathrm{帽}\mathrm{子}\mathrm{矩}\mathrm{阵}：\$\$H(\lambda )=A{(A^{\mathrm{\top }}A+\lambda I)}^{-1}{A}^{\mathrm{\top }},\hat{y}=Hy,\$\$\mathrm{那}\mathrm{么}Ecv\mathrm{的}\mathrm{速}\mathrm{算}\mathrm{公}\mathrm{式}\mathrm{就}\mathrm{是}：\$\$E_{\mathrm{loocv}}=\frac{1}{N}\sum _{n=1}^N{\left(\frac{{\hat{y}}_n-y_n}{1-H_{nn}(\lambda )}\right)}^2,\$\$\mathrm{能}O(Nd\text{^}2)\mathrm{地}\mathrm{计}\mathrm{算}\mathrm{出}\mathrm{所}\mathrm{有}\mathrm{留}\mathrm{一}\mathrm{误}\mathrm{差},\mathrm{而}\mathrm{不}\mathrm{用}\mathrm{训}\mathrm{练}N\mathrm{次}。\mathrm{我}\mathrm{们}\mathrm{可}\mathrm{以}\mathrm{用}\mathrm{使}\mathrm{得}Ecv\mathrm{最}\mathrm{小}\mathrm{的}lambda\mathrm{作}\mathrm{为}\mathrm{模}\mathrm{型}。$$

$$g^{(D)}=\text{ 在全数据集 }D\text{ 上训练得到的模型,}$$

它的总体样本外误差（对所有可能训练集D做平均）：

$$E_{\mathrm{out}}(N)={\mathbb{E}}_D[E_{\mathrm{out}}(g^{(D)})].$$

N为训练集规模。 而：

$$\begin{array}{rl}\mathbb{E}\left[\begin{array}{c}{E}_{\mathrm{cv}}\end{array}\right]& ={\mathbb{E}}_D\left[\frac{1}{N}\sum _{n=1}^N{e}_n\right]\\ & =\frac{1}{N}\sum _{n=1}^N{\mathbb{E}}_D[e_n]\\ & ={\mathbb{E}}_D[e_n]\\ & =E_{\mathrm{out}}(N-1).\end{array}$$

于是：

$$\boxed{{\displaystyle \mathbb{E}\left[\begin{array}{c}{E}_{\mathrm{cv}}\end{array}\right]=E_{\mathrm{out}}(N-1)}}$$

我们说留一法几乎无偏估计了Eout

V-fold Cross Validation

其实本质上就是Leave More-Than-One Out。 把整个数据集随机分成V fold，每一份大小约为N/V，记为 ${\mathcal{D}}_1,\dots ,{\mathcal{D}}_V$ 第v次用Dv作为验证集，其余V-1份联合起来作为训练集算出验证误差：

$$E_{\mathrm{val}}^{(v)}(g_v^{-})=\frac{1}{|{\mathcal{D}}_v|}\sum _{(x,y)\in {\mathcal{D}}_v}e(g_v^{-}(x),y).$$

总体误差就是V次误差的平均：

$$E_{\mathrm{cv}}(\mathcal{H},\mathcal{A})=\frac{1}{V}\sum _{v=1}^V{E}_{\mathrm{val}}^{(v)}(g_v^{-}).$$

V一般取5或10 （？）

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update