Week 2&3 - LR & Info Theory & Tree
Logistic Regression
Classification Problem
分类:确定输入最可能属于的类别。
形式上:对类成员资格(因变量)的后验概率进行建模,条件是输入(自变量)。
人工神经网络:每个类别一个输出单元,对于每个输入模式,
1表示与该类相对应的输出单元
0表示所有其他输出单元
最简单情况:二进制分类 → 一个输出单元
Logit regression
目标:预测给定示例属于“1”类别的概率与属于“0”类别的概率之间的差异。
- 使用logarithm of the odds, called logit or log-odds.
- 使用sigmoid function(logistic function)去将log-odds转化为probability
定义:
Odds 赔率:odds = p / (1-p)
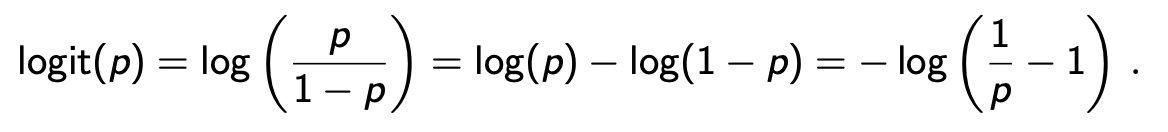
例子:52张牌,抽到黑桃的概率为13/52 = 1/4 = 0.25, 抽到黑桃的odds为 0.25 / 0.75 = 1/3
逻辑回归的假设是,logit可以用线性模型去拟合。
回顾一下线性回归:
真没啥好回顾的
PPT上讲的贼别扭,我不知道教授为什么这么讲课,把一个明明很简单的东西讲的那么数学。。。
其实逻辑回归就是在线性回归的结果上再运用一个sigmoid函数把结果变为概率,就这么简单。
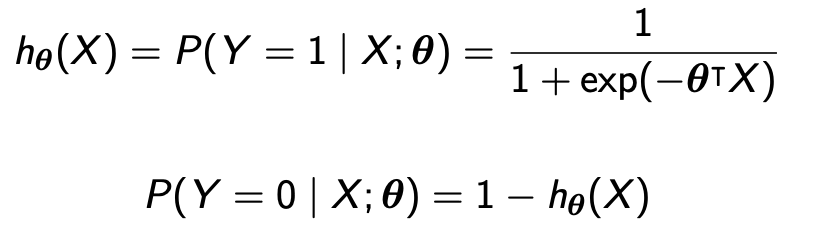
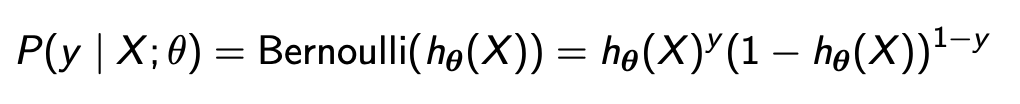
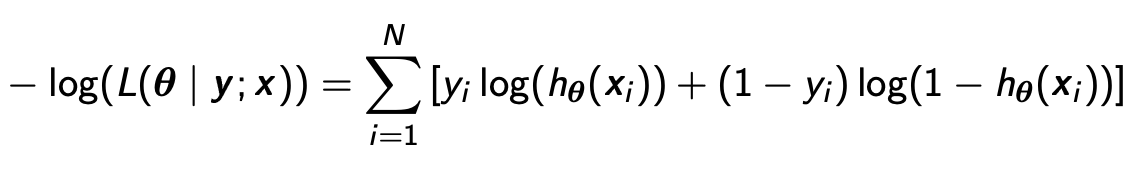
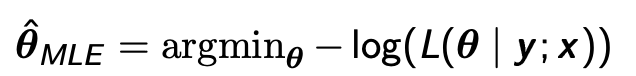
例子:Time spent and passing Math exams
已经算出来,b(intercept) = -1.2725,coefficient = 0.2064
P(Y=1) = 1 / (1 + exp(-(-1.2725 + 0.2064x1)))
Rule of ten
在拟合逻辑回归模型时,针对模型中的每一个自变量,至少需要10个具有最不频繁结果的案例。
例如,如果你的模型中有5个自变量,且你的最不频繁结果的预期概率是10%,那么你至少需要的样本大小为 10×5/0.10=500.
Information Theory
Information Theory研究的是如何量化信息。
Self Information(b自选。2为bits,e为nat or natural units,10为dits,bans,hartleys)
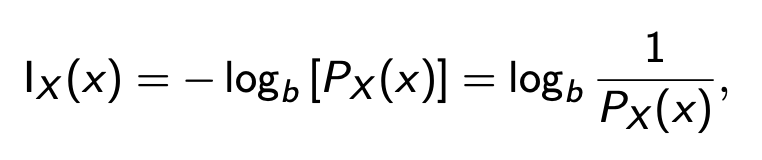
Logit用Self Information表示
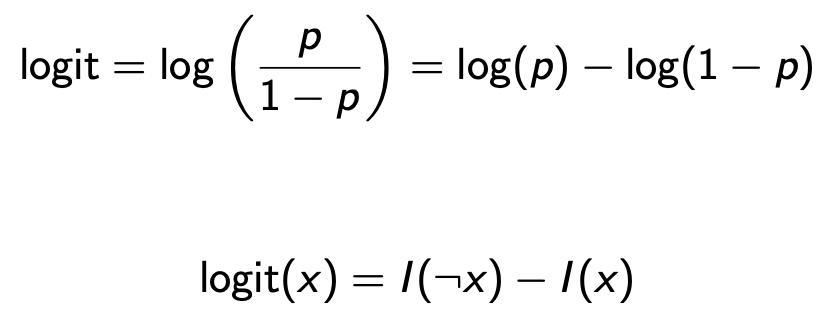
Entropy
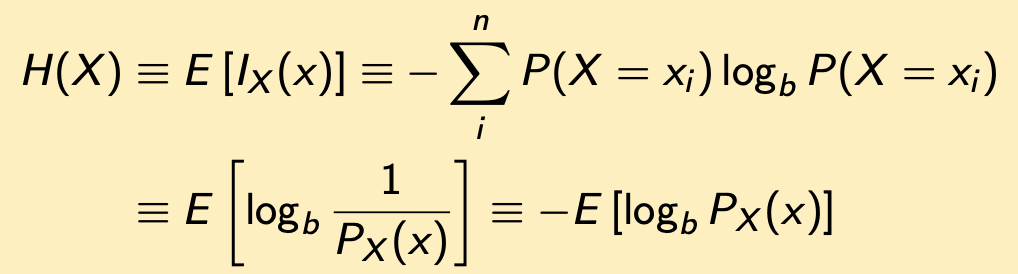
Joint Entropy
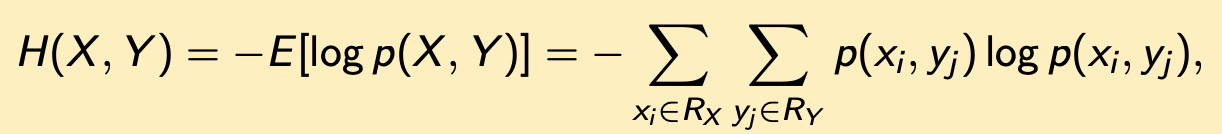
Conditional Entropy
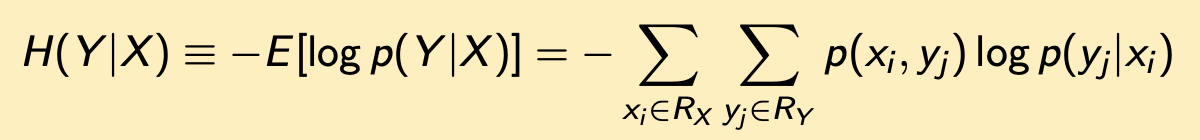
Chain rule for conditional entropy
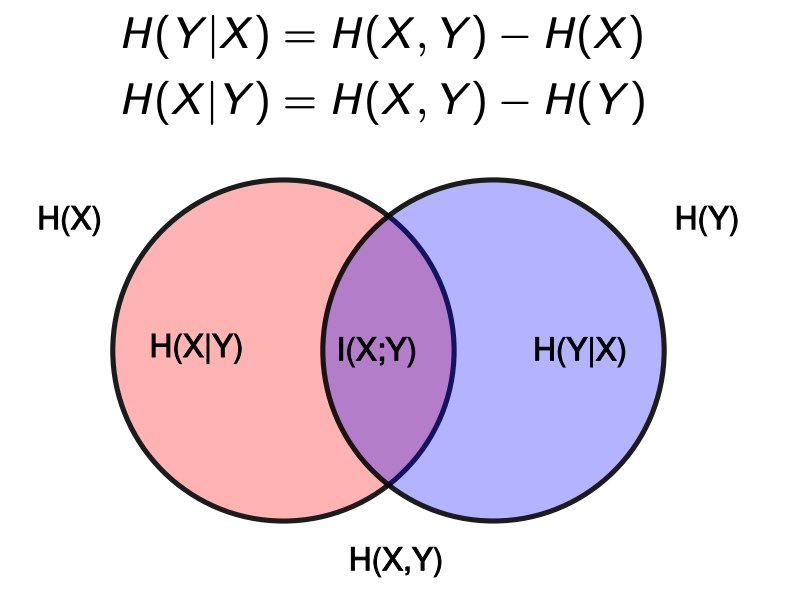
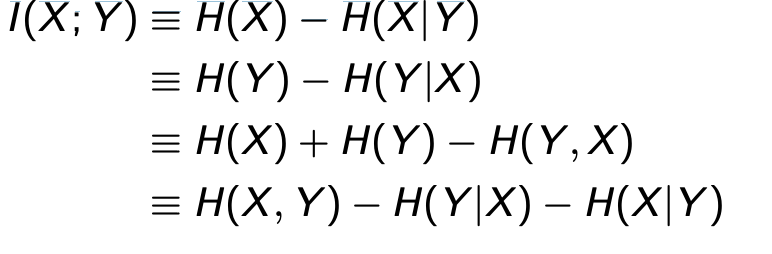
Relative entropy (KL divergence)
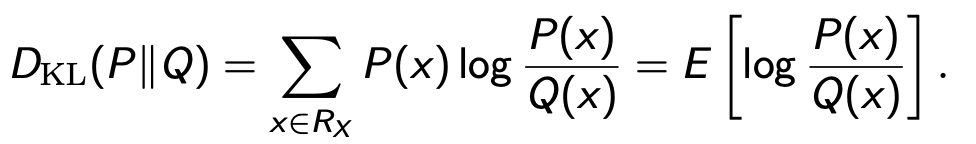
Jensen-Shannon divergence (JSD)
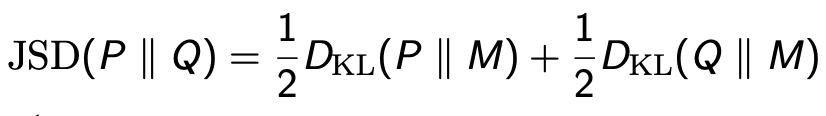
Mutual Information
“measures the information that X and Y share”
它衡量的是对其中一个变量的了解程度能在多大程度上减少另一个变量的不确定性
互信息本质上衡量了使用P(X)P(Y)来建模联合概率P(X, Y)的距离(误差)。当X和Y彼此独立时,即p(x, y) = p(x)p(y) 互信息为0
I(X;Y) = I(Y;X)




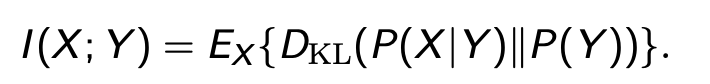
例1:正常硬币投掷正面朝上是0.5,不正常硬币是0.7。抛正常硬币为X,不正常硬币为Y
H(X) = E[I(X)] = 1/2 * log(1/(1/2)) + 1/2 * log(1/(1/2)) = log 2 = 1
H(Y) = E(I(Y)) = 0.7 * log(1/0.7) + 0.3 * log(1/0.3) = 0.36 + 0.52 = 0.88
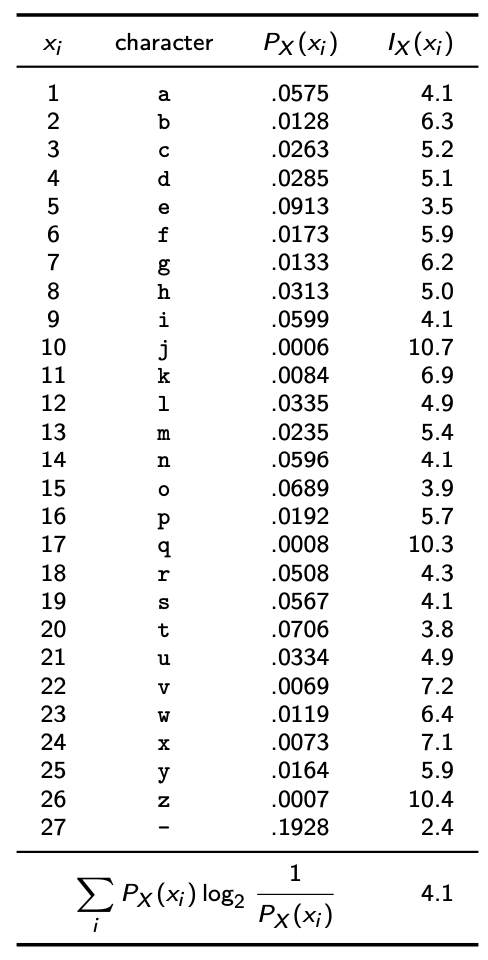
例2:将英语语言视为一个离散随机变量X,其范围RX = {1, 2, 3, . . . , 27},其中值1-26代表26个字母(a-z)的出现,27代表空格字符(用于分隔两个单词)。
计算entropy
H(X) = 1/8 * log8 + 3/4 * log(4/3) + 1/8 * log8 = 1.061 bits
H(Y) = 1/2 * log2 + 1/4 * log4 + 1/4 * log4 = 1.5 bits
H(X,Y) = 1/16 * log(16) + 3/8 * log(8/3) + 1/16 * log(16) + 1/16 * log(16) + 3/16 * log(16/3) + 3/16 * log(16/3) + 1/16 * log(16) = 2.436
H(X|Y) = H(X,Y) - H(Y) = 2.436-1.5 = 0.936 bits
H(Y|X) = H(X,Y) - H(X) = 2.436-1.061 = 1.375 bits
I(X;Y) = H(X) - H(X|Y) = 1.061-0.936 = 0.125 bits
Decision Tree
预测模型:由以下组成的树结构:
根或内部节点:一个独立变量(也称为特征或属性)
叶子:依赖变量的结果
分支:规则(或决策)
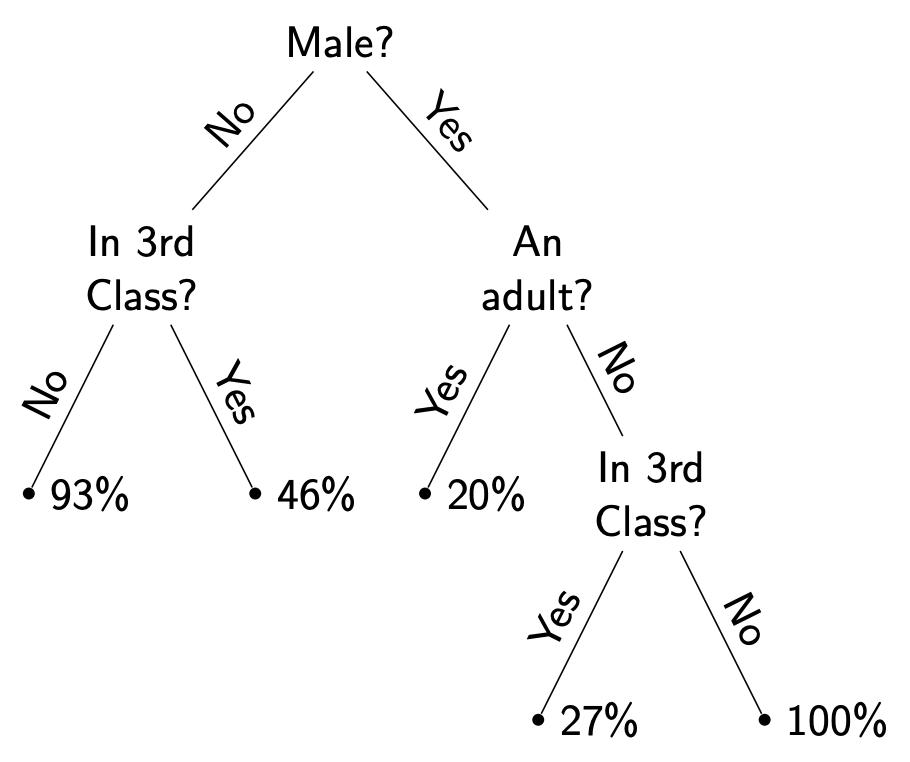
问题:如何构建决策树? 如何从数据中学习结构?
答案:给定一个数据集,算法将相似的样本分组和标记,并寻找最佳规则来分割不同的样本,直到它们达到一定程度的相似性。
拆分样本有两种方法。在CART中,用了Gini index
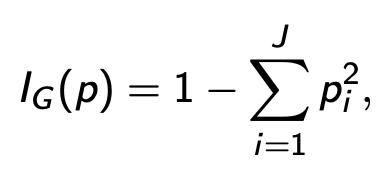
而在ID3算法和C4.5算法中用到了Information Gain, 其实就是mutual information
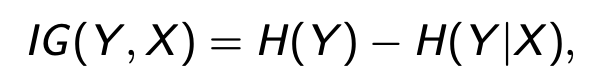
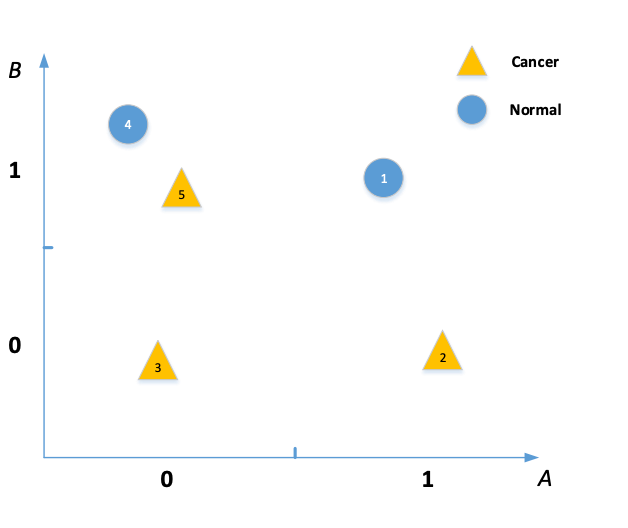
实例:使用Information Gain来构建决策树

我们只研究其中的AB两个因素
首先,计算Y的熵,Y是是否有癌症。0为没得,1为得了
然后,算出Y和A,Y和B,Y和C的IG
记住,IG一般通过H(X,Y)-H(X|Y)或者H(X)-H(X|Y)获得
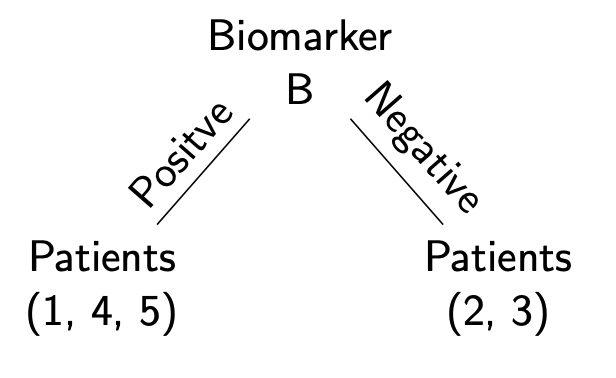
由于IG(Y,B)最大,所以用B作为分割。
对于具有两个以上数值(称为分类变量)和连续随机变量的一般离散随机变量,我们需要搜索最佳值,称为切割点、切点或阈值来最大化信息增益。
缺点:
不稳定:数据的微小变化可能导致最优决策树结构的大幅度变化。
相对不准确:许多其他预测器,如支持向量机和神经网络,比具有类似数据的决策树表现更好。
解决方案:决策树集成:
随机森林
梯度提升(例如XGBoost)
Mutual Information Feature Selection

在这个特征选择过程中,算法试图选择与目标变量 Y 最相关的 K 个特征。这个过程可以总结如下:
- 初始化:将 F(特征集)设置为所有可能的特征 X,将 S(选中的特征集)初始化为空集。
- 确定 ( f_{max} ):在所有特征 X 中找到与目标变量 Y 互信息最大的特征 (X_i )。
- 更新 F 和 S:从 F 中移除 ( f_{max} ),并将 ( f_{max} ) 添加到 S 中。
- 重复步骤 2 和 3,直到 S 中的特征数量等于 K。在重复步骤中,选取的是在考虑已选特征集 S 的条件下,和 Y 的条件互信息最大的特征,同时还考虑了特征之间的冗余,通过减去一个系数 β 乘以特征集 S 中每个特征与当前候选特征的互信息的和。这是为了减少选择高度相关的特征,从而增加特征集的多样性。
算法结束时,S 将包含与目标变量 Y 最相关的 K 个特征,同时尽量减少了特征之间的冗余信息。这种方法通常用于减少数据维度、提高模型训练效率、避免过拟合,并可能提高模型的泛化能力。
Exercise Question



-0.77 + 0.23*0.5 - 1.18 = -1.835
p/1-p = exp(-1.835) = 0.1596
p = 0.1596-0.1596p p = 0.1376
OR_E = odd(E=1) / odd(E=0) = exp(-0.77+0.23-1.18) / exp(-0.77+0.23) = 0.31
OR_H = odd(H=h+delta) / odd(H=h) = 1.25^(delta)
如果客户添加额外的数据计划,终止合同的几率将增加0.31,这意味着客户终止合同的几率会降低3倍。
如果客户平均时间增加一小时,则终止合同的几率会增加1.25倍。
从分析中我们可以向老板建议,顾客花费的时间越多,他们终止合同的可能性就越大,这意味着公司应该改善其电信服务/价格。然而,简单地说服他们订阅额外数据计划,则更有可能留下来。

注意 C_(100)^(55) == (下55上100)
L = C_100^55 p^55 (1-p)^45
Log(L) = log + 55logp + 45log(1-p)
Log(L)` = 55/p - 45/1-p = 0
55/p = 45/1-p -> 55-55p = 45p -> 100p = 55 -> p=0.55

(a1) 互信息背后的基本动机是衡量两个随机变量X和Y共享的信息。换句话说,它衡量了知道其中一个变量如何减少对另一个变量的不确定性。
The basic motivation of mutual information is to measure the shared information between X and Y. In other words, it measures onces you know one variable, how much uncertainty reduced for another variable.
(a2) The two lines in the loop are used to select K features. In this loop, we also find the feature fmax which achieves the maximum mutual information I among all the remaining independent variables in set F . However, because some features highly correlated with each other, selecting them will increase the number of features but does not improve the prediction. Therefore, we need to make sure there must be minimal redundancy between the candidate feature Xi and the set of selected features S. That's exactly the second term of the equation ( fmax) You then add this feature into S and then subtract it from set F and repeat until we got K features".
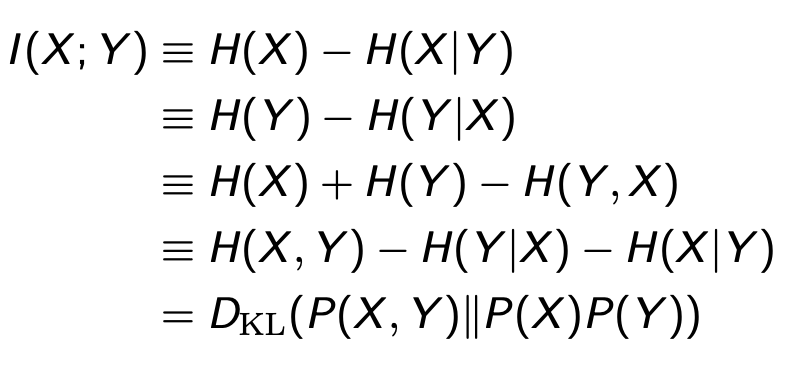
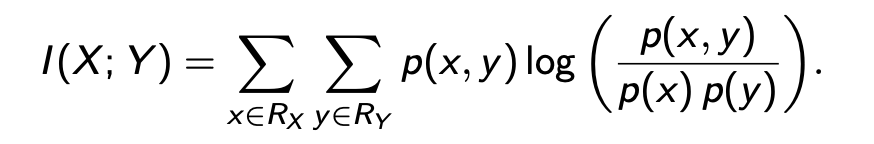
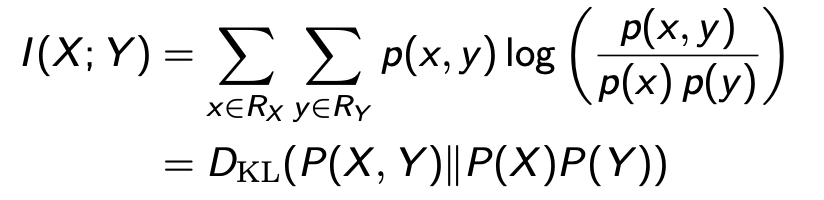
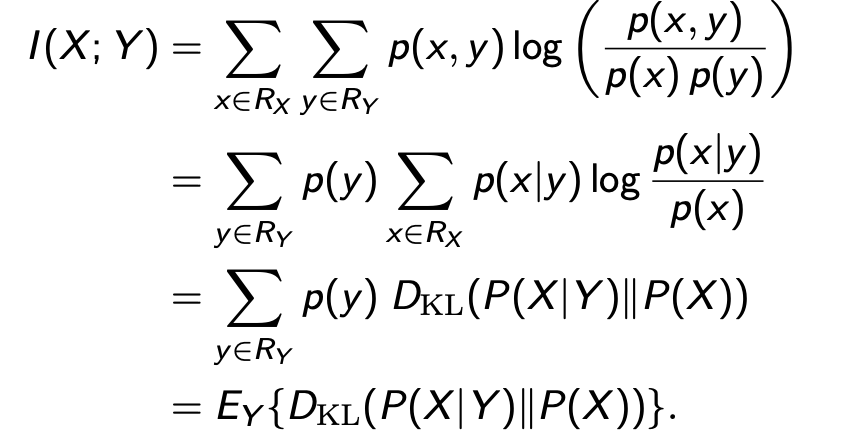
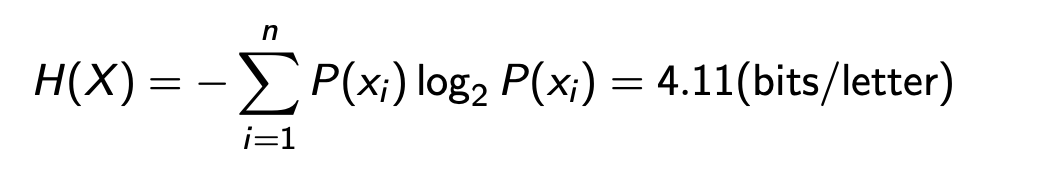

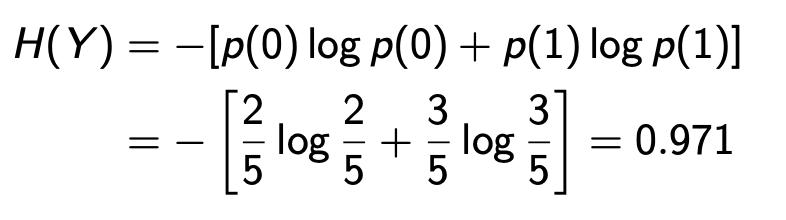
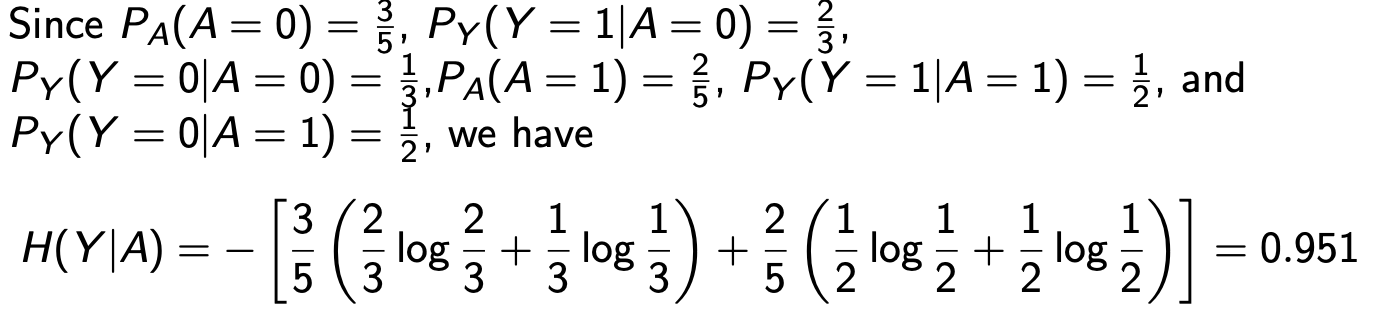
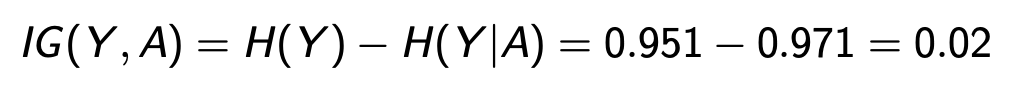
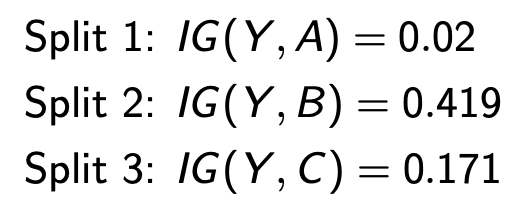
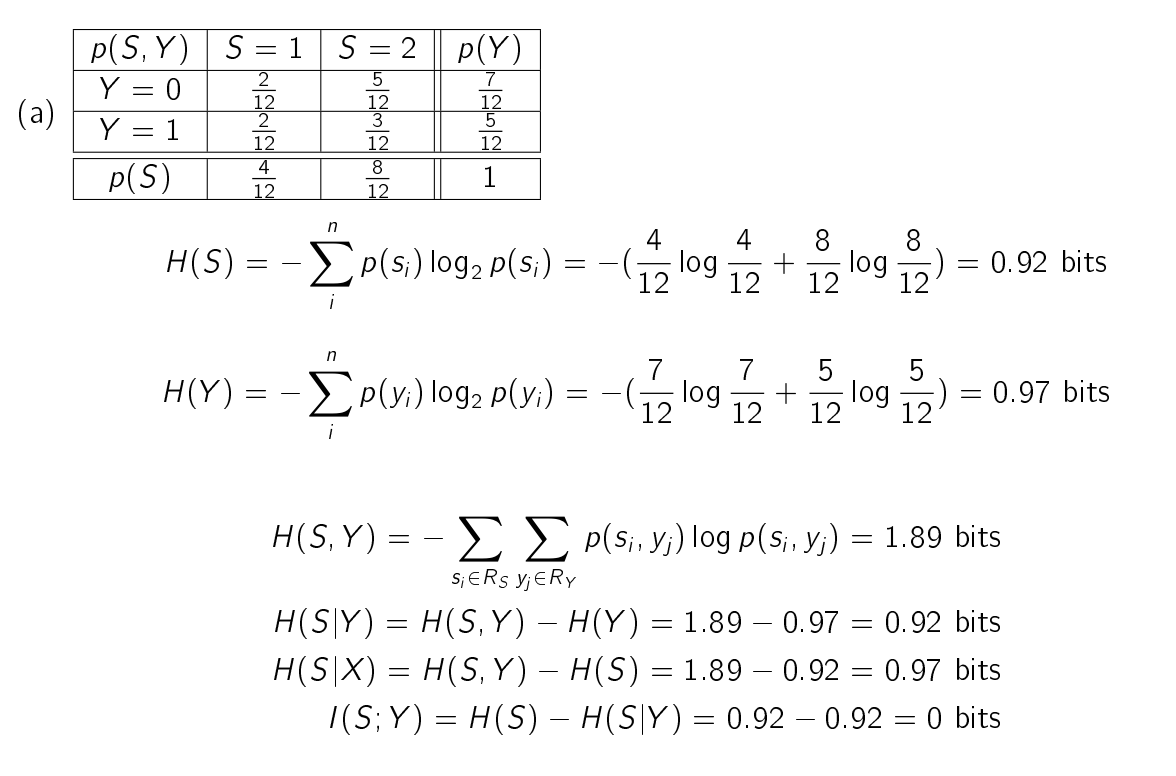
 Larry Shi
Larry Shi