Transformer

字数

3313 字

阅读时间

14 分钟

Transformer是利用了Attention机制 的一种架构，在当下应用广泛，改天灭地。

Scaling Law

这部分引用了 【LLM 10 大观念-1】缩放定律Scaling Law 定义：我们可以用模型大小、数据集大小、总计算量，来预测模型最终能力。（通常以相对简单的函数形态，例如：线性关系） 对于研究员而言，早就具备一些关于 Scaling 的直觉。像是：Model 越大、Data 越多，performance 都会随之提升 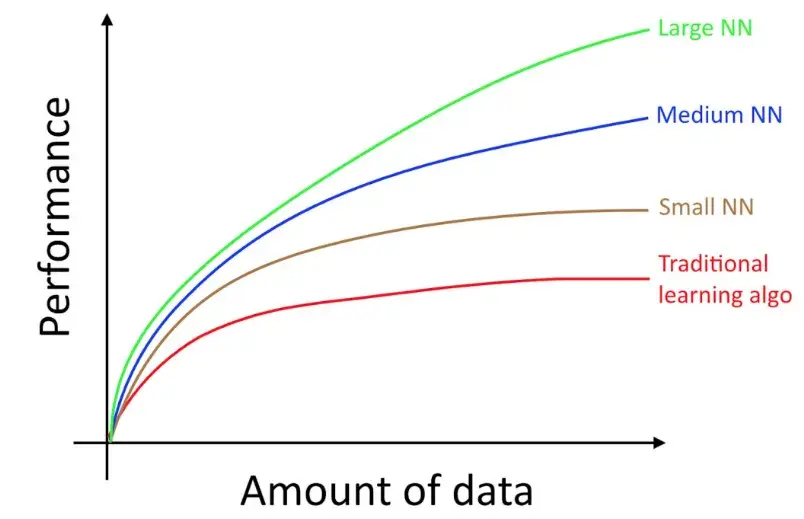而 DeepMind 的 Chinchilla 提出的 Chinchilla Scaling Law 用数学建模了Scaling Law 当我们有了Scaling Law的直觉后，我们就会很容易想到两个问题：

1. Return（收益）：在固定的训练计算量之下，我们所能得到的最好性能是多好？
2. Allocation（分配）：我们要怎么分配我们的模型参数量跟 Dataset 大小。（假设计算量 = 参数量 * Dataset size，我们要大模型 * 少量 data、中模型 * 中量 data、还是小模型 * 大量 data） 那么这时，我们就需要一个比较准确的数学建模来帮我们理解问题。那么得到的结论如图：

$$L(N,D)=E+\frac{A}{N^{0.34}}+\frac{B}{D^{0.28}},E=1.69,A=406.4,B=410.7$$

其中N 是模型参数量、D 是数据量，L是Perplexity。 那么给了我们什么启示呢？

1. 数据量（Tokens 数）应该要约等于模型参数量的 20 倍
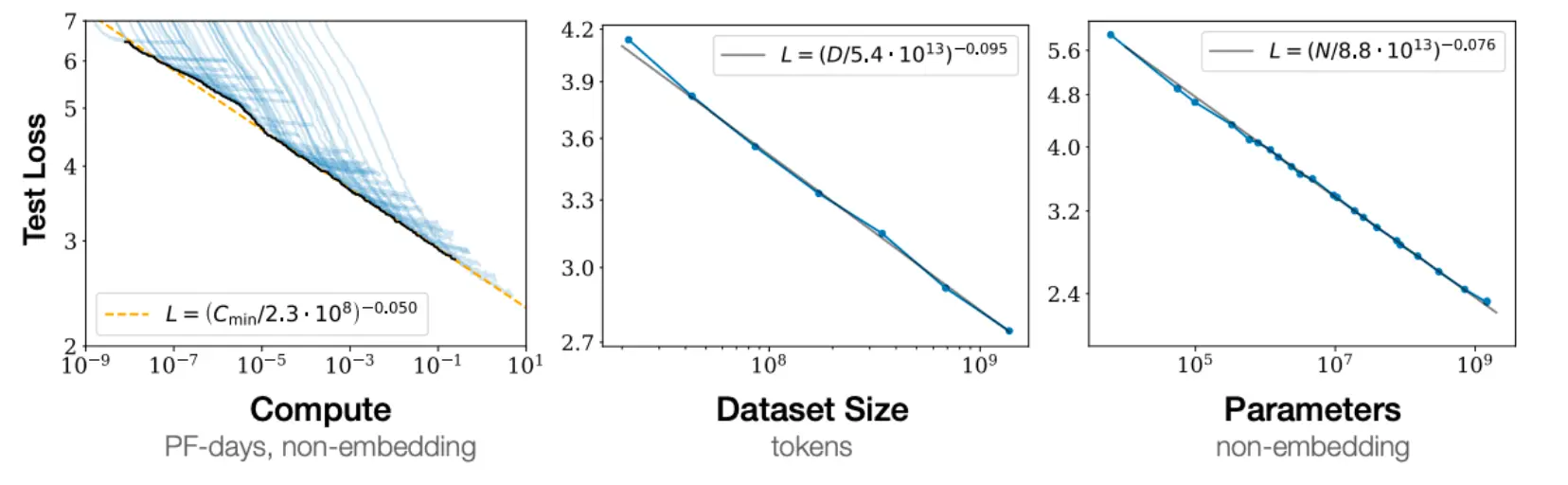
2. 数据量跟模型参数量要同比放大（例如：模型放大一倍，数据也要跟着增加一倍） OpenAI的文章指出，参数量，数据集大小，训练时间都和Loss有一种幂律关系（即，$L=k\cdot x^c$ ）

RNN to Transformer

RNN在NLP成功的de facto是采用 bi-LSTM去将句子encode。当然，你可以选择使用attention机制在解码的时候选择想要的h。 Transformer的作者在设计的时候，有三个愿望：

最小化（或至少不增加）每层的计算复杂度

当序列长度（n）<< 表示维度（d）时，每层的复杂度对于Transformer而言比我们迄今所学的循环模型要低。

最小化任意一对单词之间的路径长度，以便促进长距离依赖关系的学习

RNN从左到右展开，就地编码每个单词，这的确是一种很棒的heuristic方法，离得近的单词互相影响意思。但问题是，RNN要花O(sequence length) 步去让离的远的词交互。 这就意味着，学习长距离依赖关系很困难（因为梯度问题！） 传统序列模型假设单词的顺序是线性的（从左到右或从右到左），这对捕捉非线性依赖关系（如语法树中的依赖）非常不利。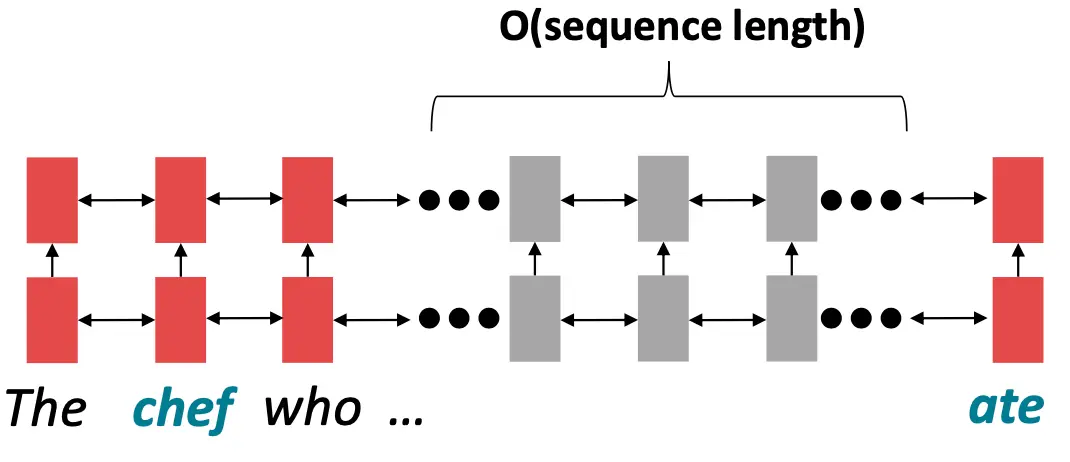

最大化可以并行化的计算量

RNN中，序列数据的处理具有时间步依赖性，这就导致了：

• 只有当 ht−1​ 计算完成后，才能开始计算 ht​，这就导致了不能并行，序列越长，计算所需时间越多。
• 对大规模数据集的训练不友好，序列长度增加，RNN 的顺序计算会显著拖慢训练速度。内存限制也会阻碍长序列的批量训练（batch training）。

Transformer 导言

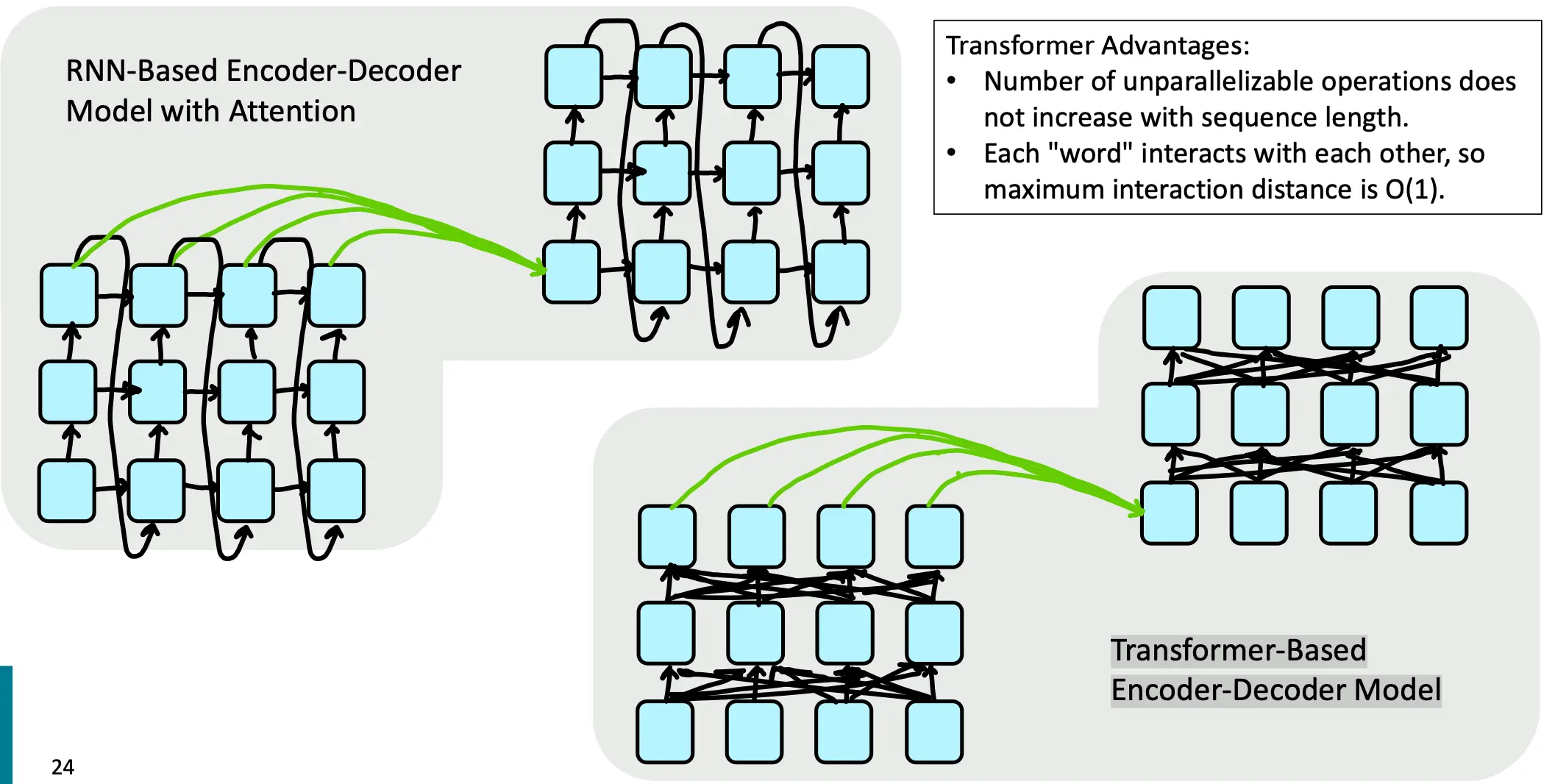
Transformer的核心机制是self-attention Attention认为要被查找的原词的向量表示为query，并从一堆values中找到相对应的信息。上次的seq2seq最后讲的attention 6 - Attention 是属于decoder to encoder结构。而self-attention是属于encoder to encoder结构 (或者decoder - decoder结构), 是each word attends to each other word within the input(or output) 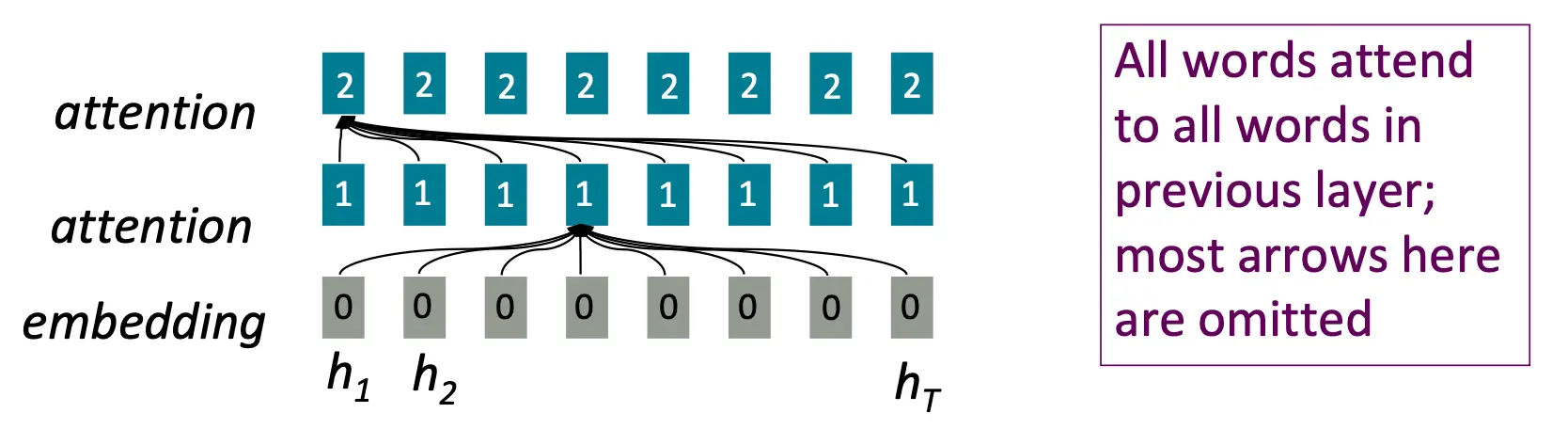这图中表示了一个多层的 self attention 结构，每一层都包含一个自注意力模块，每个单词的表示通过自注意力机制与其他单词交互，生成新的表示。

如果现在要用到encoder-decoder中，transformer based就和rnn based attention就有区别了：

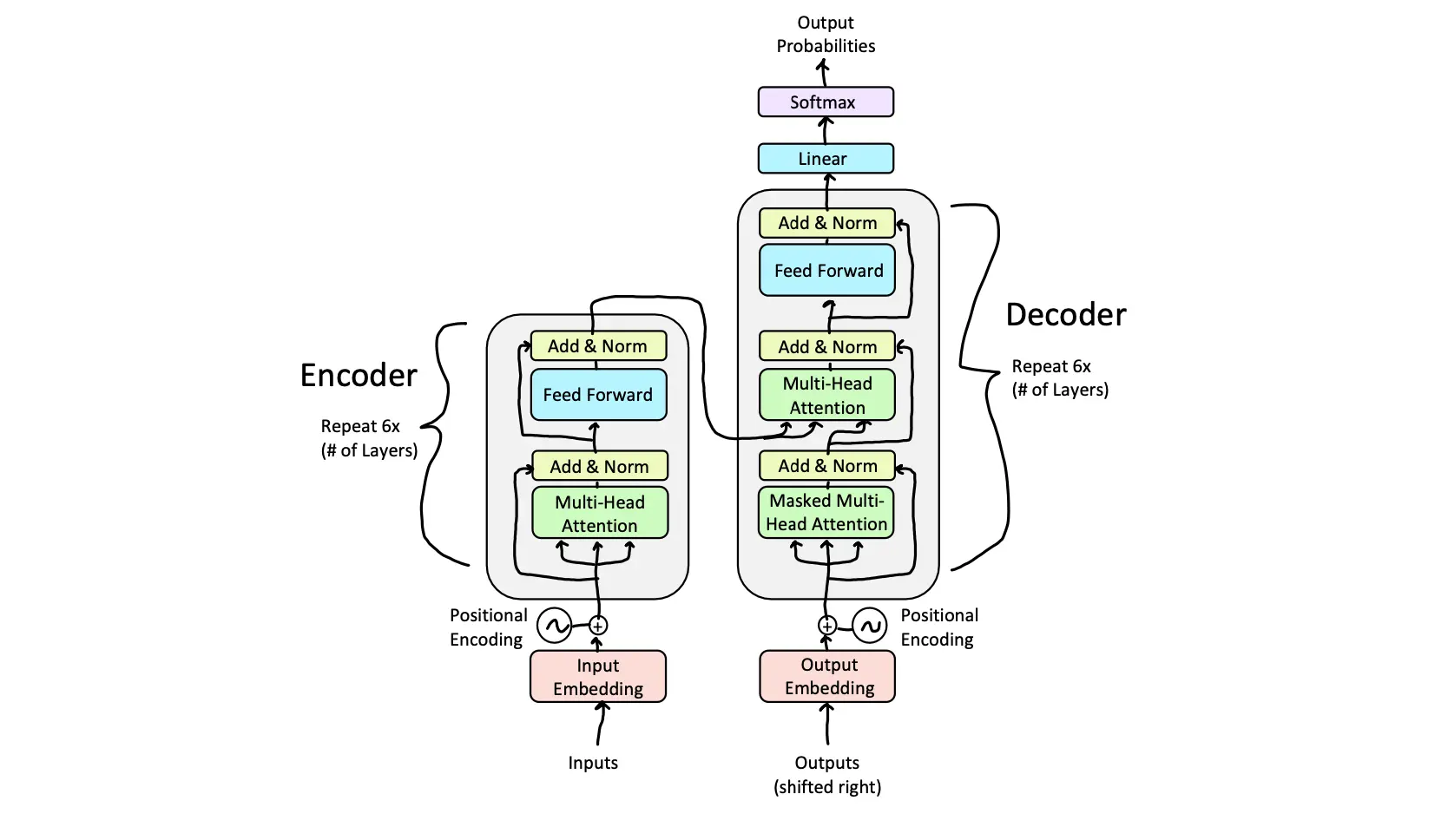
Transformer Encoder

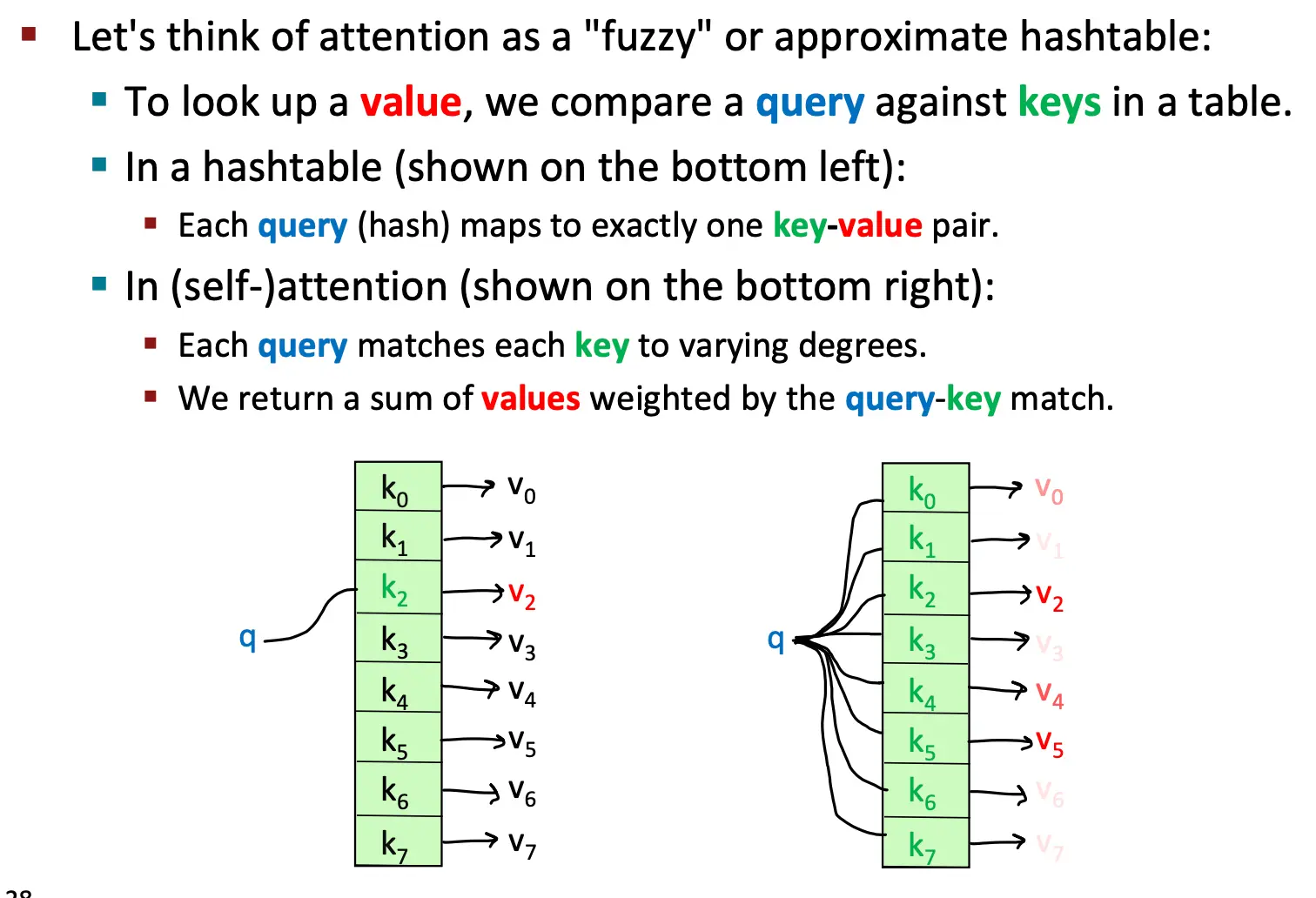
Self-Attention

但Attention is not all you need。因为Self-Attention 的局限性。Self-Attention 机制本质上是对输入序列中每个位置的值向量（value vectors）进行加权平均。它本身是线性的，没有非线性变换。这意味着 Self-Attention 只能在一定程度上捕捉输入序列的关系，但缺乏足够的表达能力来处理复杂的模式或非线性特征。我们可以通过在 Self-Attention 的输出之后，添加一个前馈层（FF），通过非线性激活函数（如 ReLU）引入非线性变换，从而增强模型的表达能力。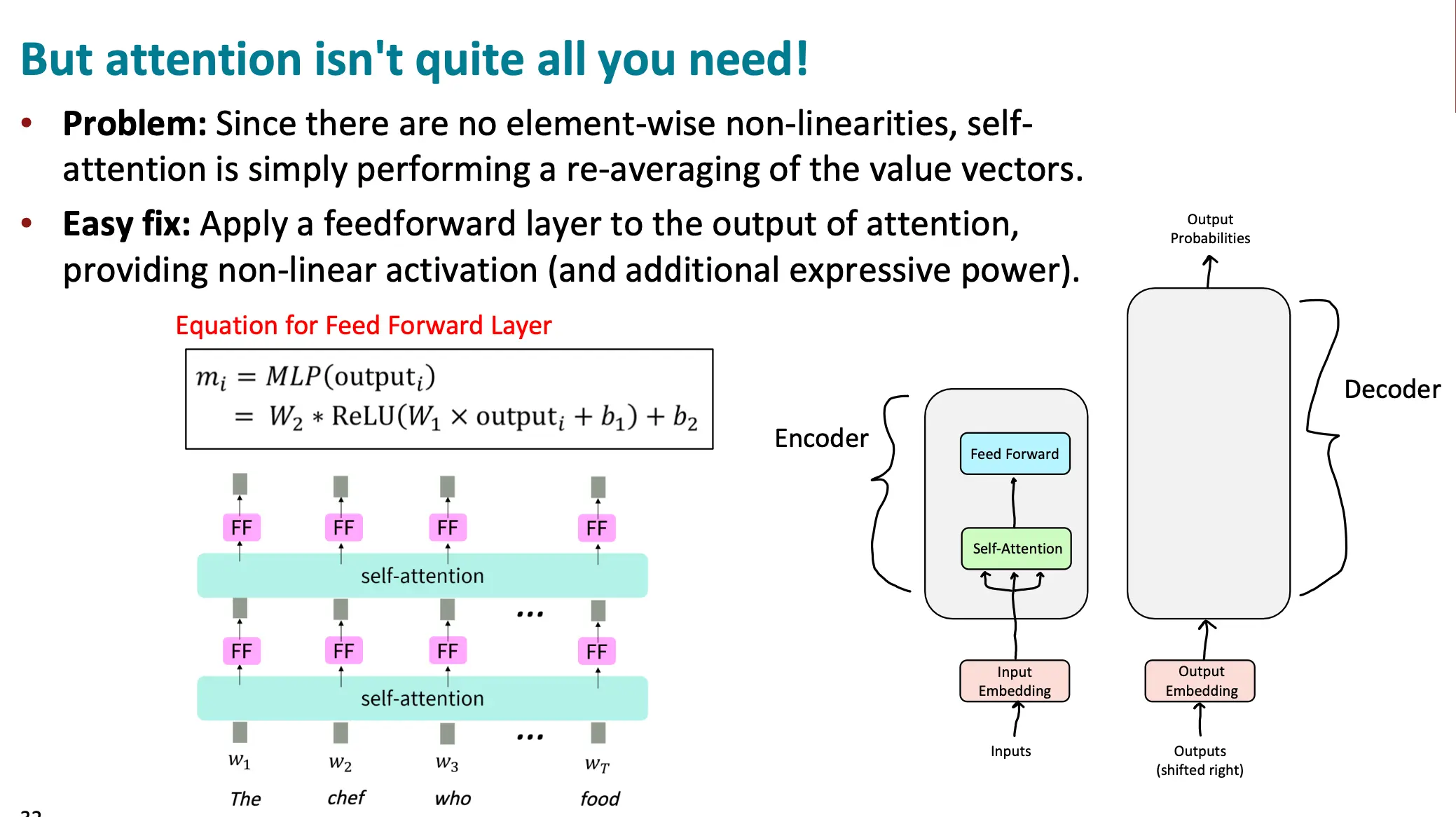

怎么训练深层的这种transformer呢？

1. 残差链接

2. LayerNorm

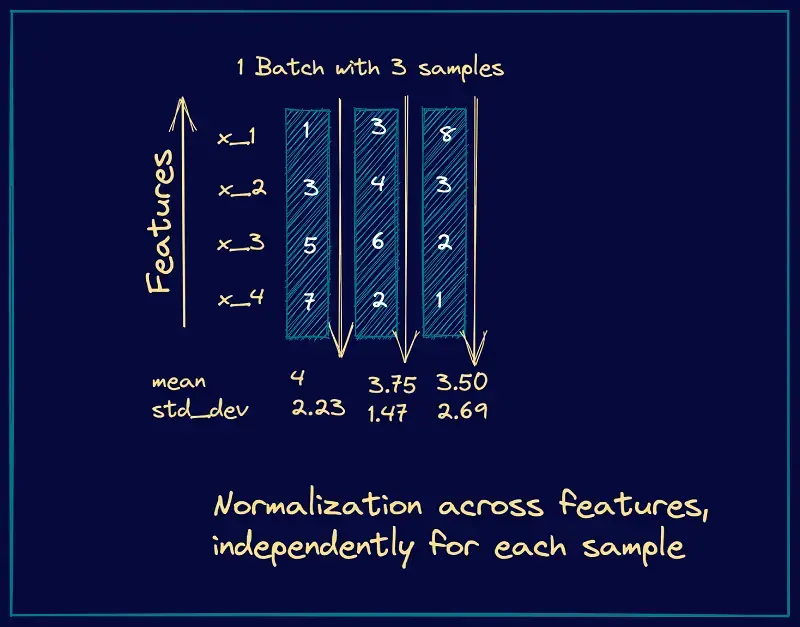
在前一层后一层中间加层归一化，就把前一层的输出求均值方差归一化之后再给第二层。 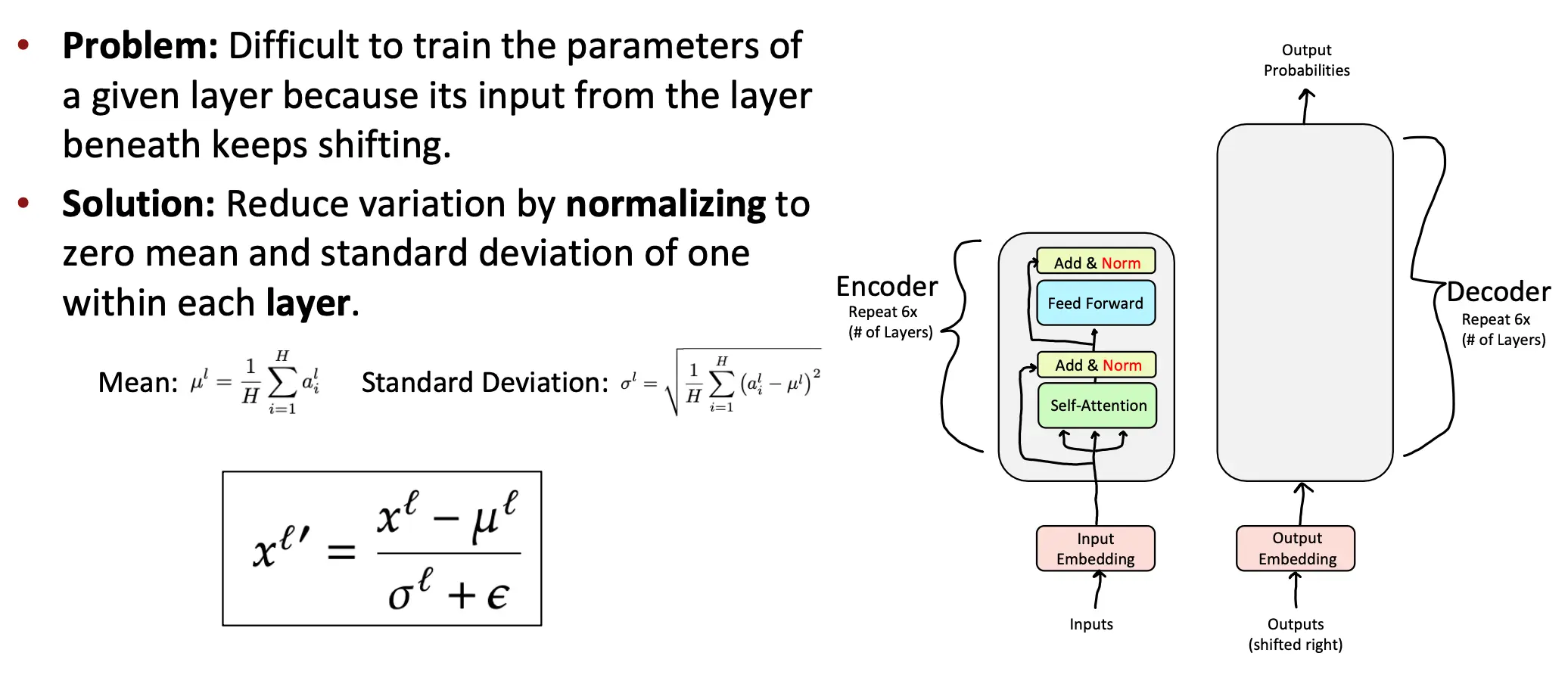Minibatch Norm & LayerNorm

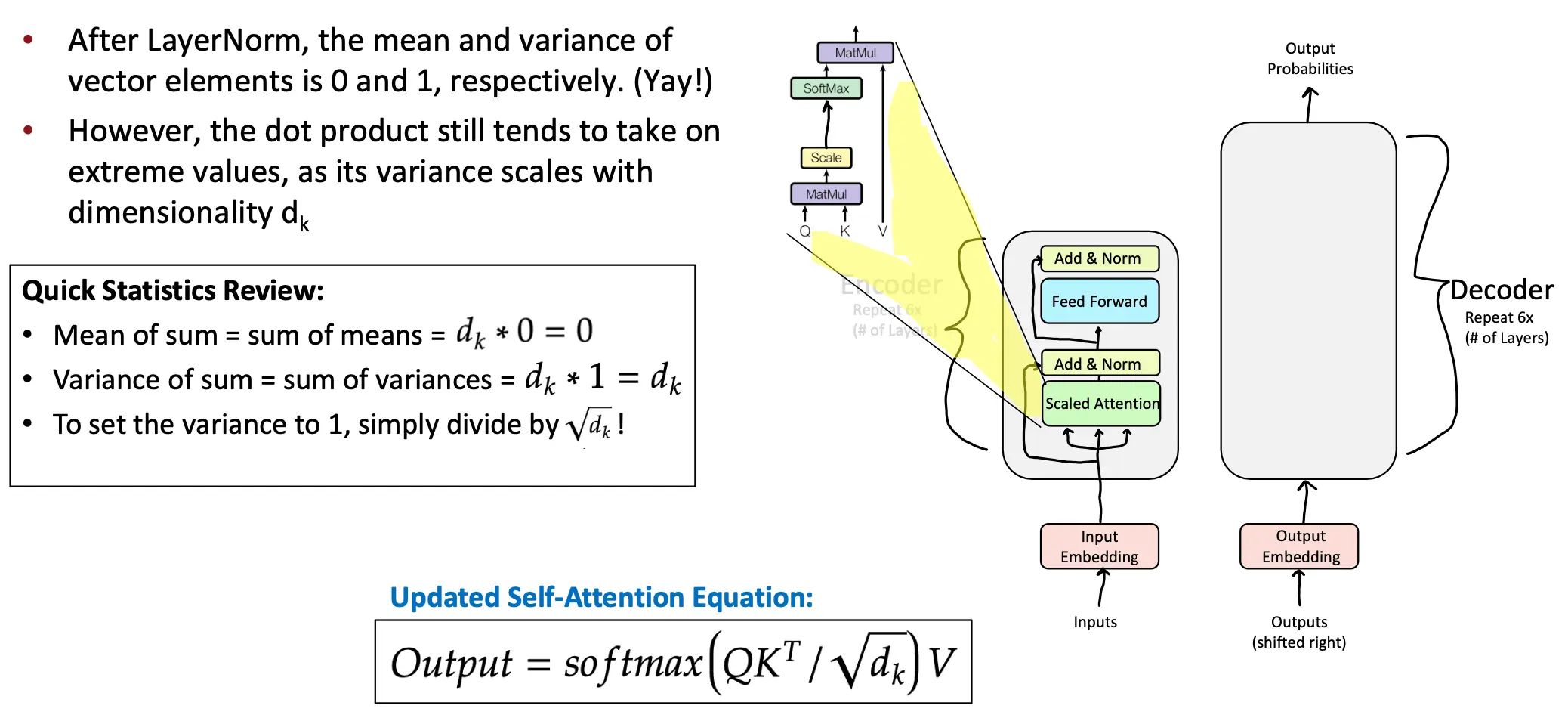
3. Scaled Dot Product Attention

点积操作的结果会随着Q K向量维度 (dk) 的增加而变得很大，从而导致数值不稳定性。这是因为：

• 点积是多个值的累积和，维度越高，累积的值越多，结果的方差会随着 dk 增大而增大。如果点积结果的方差是 dk​，为了将方差缩放到 1，需要将点积结果除以 sqrt(dk)​​。这是因为缩放一个随机变量的标准差会影响其方差。 为什么点乘结果的方差是dk呢？因为在QK点乘之前，已经进行过层归一化了，这就会让Q中q1...qn的方差，以及K的方差都是1. 那么q1 * k1 的方差也是1，而方差是累加的，所以维度是dk，那么方差也就是1 * dk = dk。$$Q\cdot K=\sum _{i=1}^{d_k}{q}_i{k}_i$$在除以根号dk后，方差就又回到1了，好结果。
• 点积结果的方差过大，输入 softmax 的值会变得极端（过大或过小），导致梯度消失或梯度爆炸问题。 所以，引入 缩放因子

位置编码

最后还有一个问题，就是要赋予位置。思考这句话Man eats small dinosaur，顺序很有必要。所以要进行位置编码。 为每个位置 i 生成一个多维向量 pi​。i 是序列中的位置索引（例如，第 ii 个单词）。d 是编码向量的维度（与 Transformer 的嵌入维度一致）。j 是维度索引（从 00 到 d/2−1d/2−1）。100002j/d 控制不同维度的正弦和余弦函数的周期。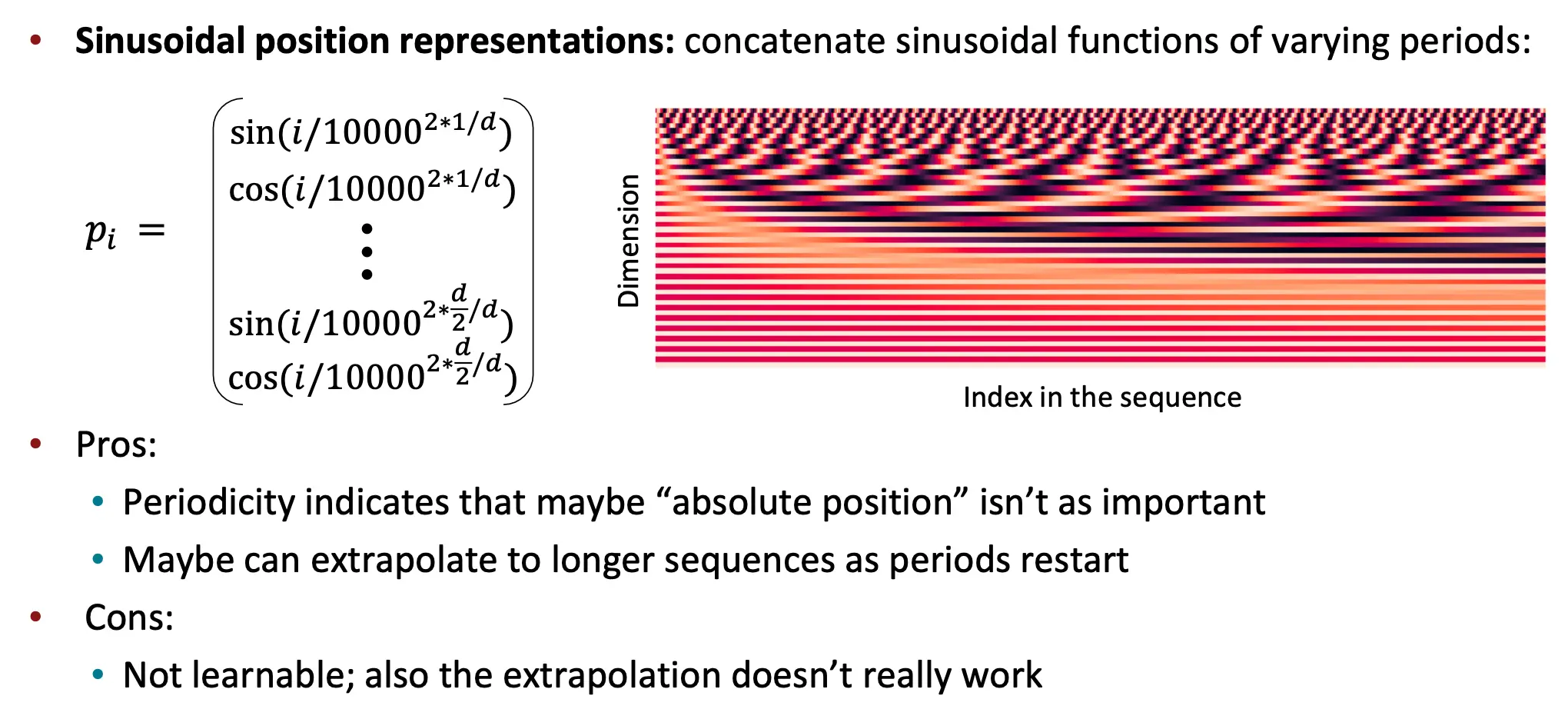

优点（Pros）

1. 周期性捕捉相对位置关系：
   • 正弦和余弦的周期性使得模型可以捕捉序列中相对位置的关系，而不仅仅是绝对位置。
   • 这表明绝对位置可能并不重要，模型更关注相对位置。
2. 外推能力：
   • 理论上，正弦位置编码可以推广到比训练时更长的序列，因为正弦和余弦函数是无限周期的。

---

缺点（Cons）

1. 不可学习：
   • 正弦位置编码是固定的，不能通过训练调整。这可能限制了模型对某些特定任务的适应能力。
   • 可学习的位置编码（Learnable Positional Encoding）可以在训练过程中优化，但正弦编码无法做到这一点。
2. 外推能力有限：
   • 尽管正弦编码理论上可以外推到更长的序列，但实际效果并不好，因为模型可能无法很好地利用这些周期性信息。

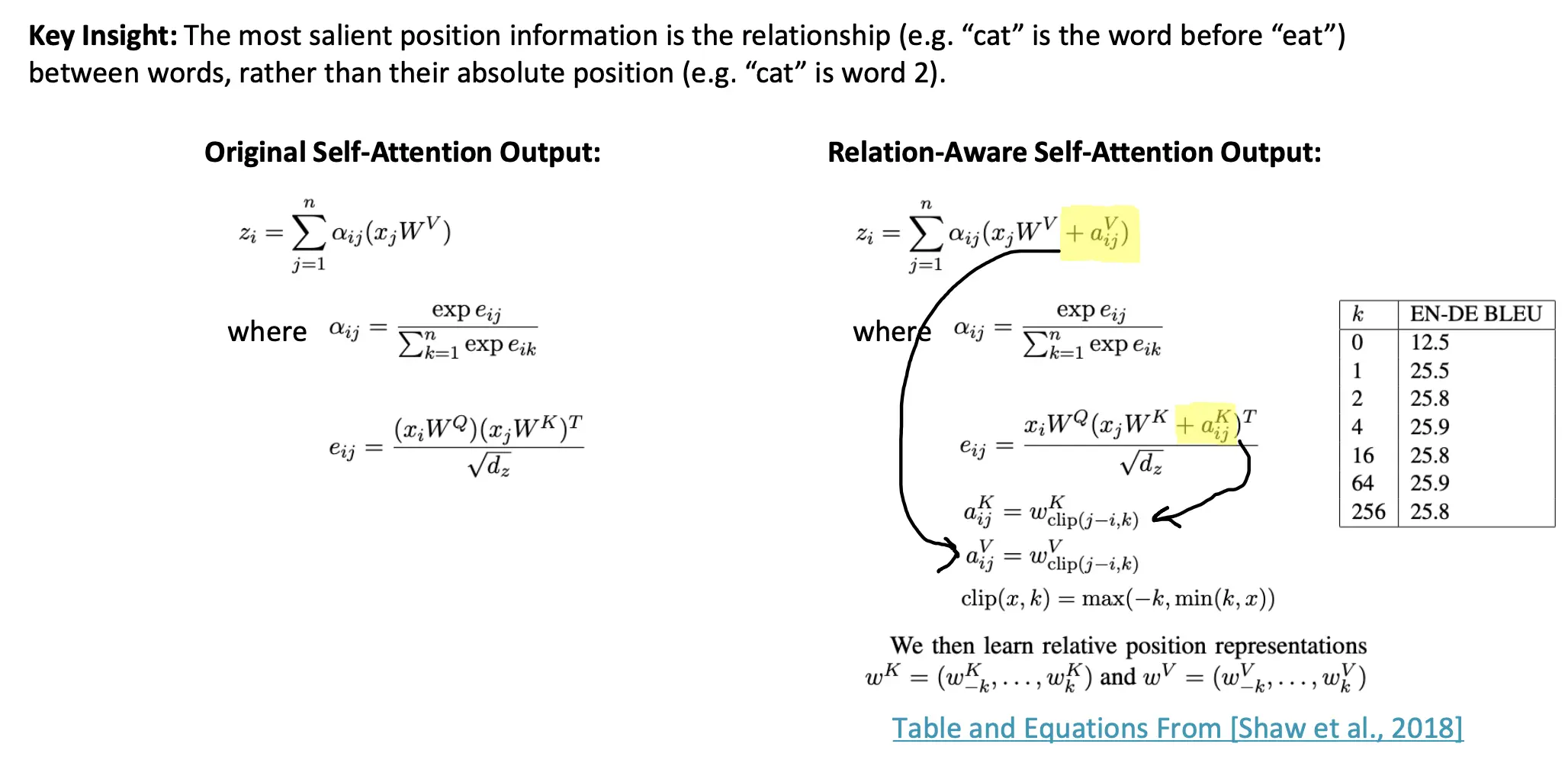
相对位置编码

传统的 Transformer 使用绝对位置编码（如正弦位置编码）来表示序列中每个位置的位置信息。然而，许多任务中更重要的是词与词之间的相对关系，而非绝对位置。例如：

• 在句子 "The cat eats" 中，"cat" 是 "eats" 的前一个词，这种相对位置关系比 "cat" 在句子中的绝对位置更重要。 这张幻灯片提出了一种改进的方式：将相对位置编码引入到自注意力机制中，以更好地捕捉词与词之间的相对关系。 相对位置偏置 aijK​ 和 aijV​ 的具体定义如下：

$$\begin{array}{rl}& a_{ij}^K=w_{\mathrm{clip}(j-i,k)}^K\\ & a_{ij}^V=w_{\mathrm{clip}(j-i,k)}^V\end{array}$$

• j−i：表示第 jj 个位置相对于第 ii 个位置的偏移量（即相对位置）。
• clip(j−i,k)：将相对位置限制在 [−k,k] 的范围内，避免过大的偏移量。
• wK 和 wV：分别为键和值的相对位置权重，这些权重是可学习的参数。

原始的自注意力输出公式如下：

$$z_i=\sum _{j=1}^n{\alpha }_{ij}(x_j{W}^V)$$

注意力权重 (\alpha_{ij}) 是通过 softmax 正规化后的注意力分数 (e_{ij}) 得到的：

$${\alpha }_{ij}=\frac{\exp (e_{ij})}{\sum _{k=1}^n\exp (e_{ik})}$$

而 (e_{ij}) 是由查询向量和键向量的点积计算得到的：

$$e_{ij}=\frac{(x_i{W}^Q)(x_j{W}^K{)}^T}{\sqrt{d_z}}$$

在引入相对位置编码后，自注意力的公式变为：

$$z_i=\sum _{j=1}^n{\alpha }_{ij}(x_j{W}^V+a_{ij}^V)$$

其中，注意力分数 (e_{ij}) 也被修改为：

$$e_{ij}=\frac{(x_i{W}^Q)(x_j{W}^K{)}^T}{\sqrt{d_z}}+a_{ij}^K$$

Multi-Headed Self-Attention: k heads are better than 1!

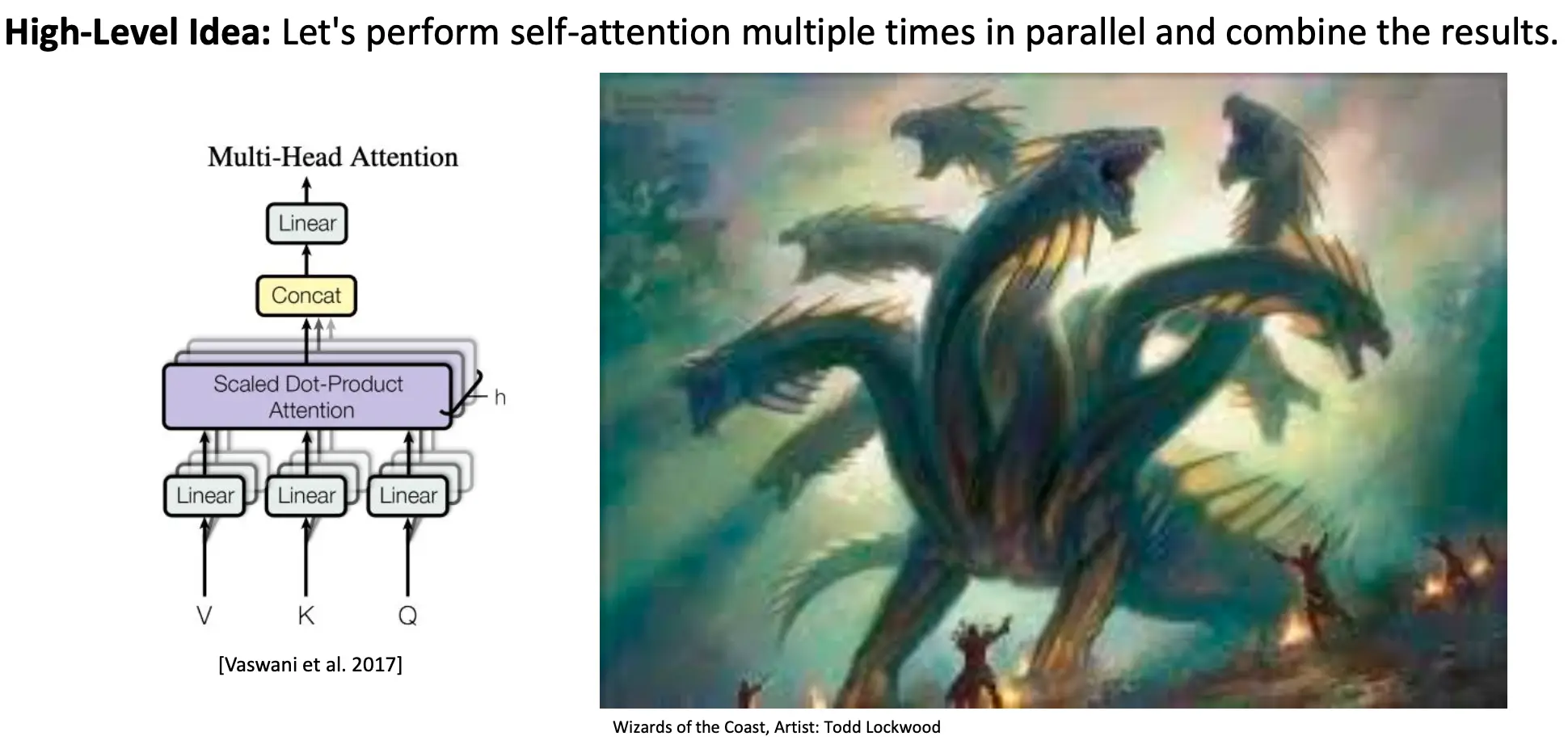
在真实的情况下，一个词可能由于不同的原因focus on不同的词，所以我们希望用多头，不同的头去处理一个层面的原因。

Transformer Decoder

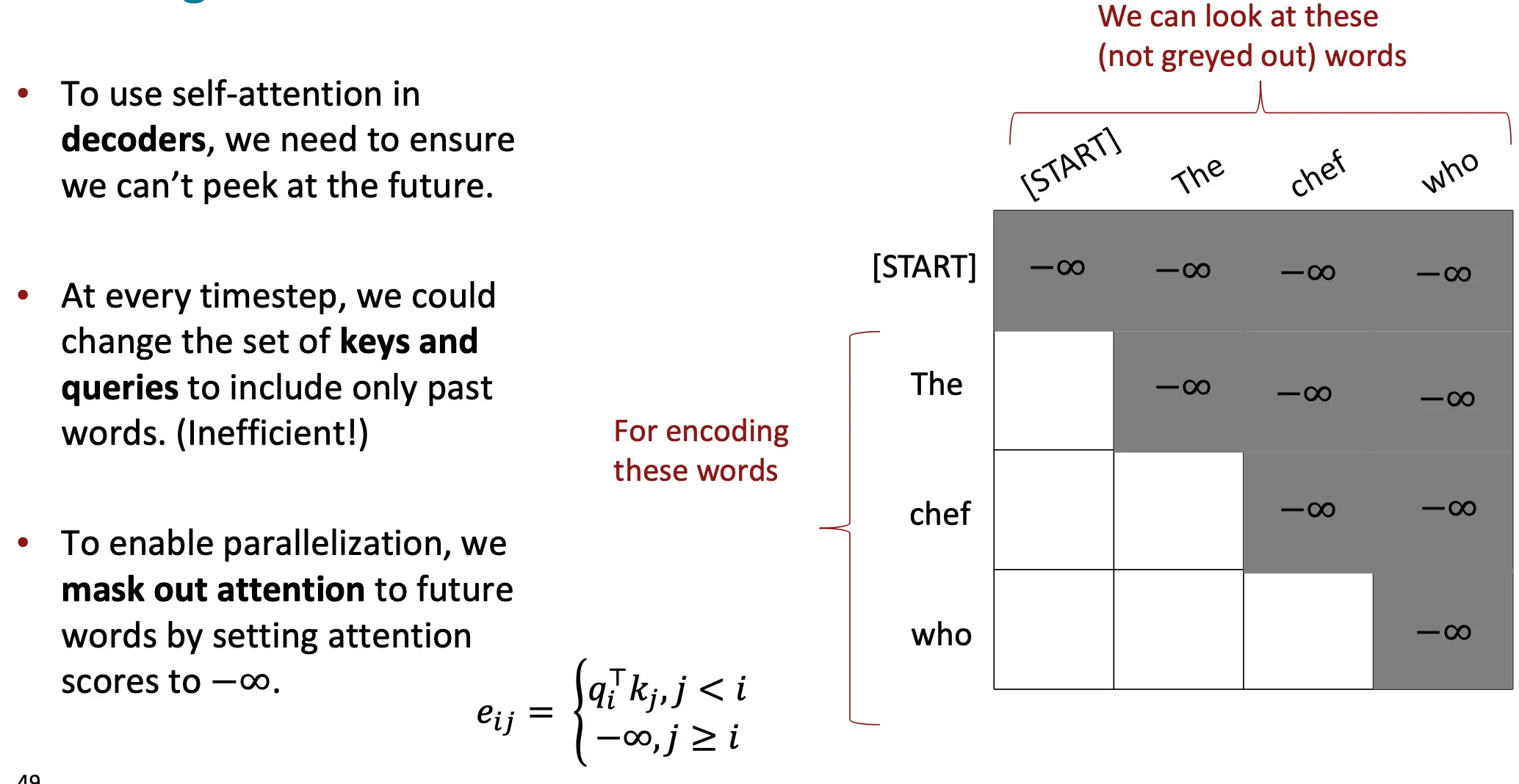
在序列生成任务（如机器翻译或文本生成）中，解码器需要逐步生成目标序列的每个词。例如： 在生成第 t 个词时，解码器只能看到已经生成的前 t−1 个词，而不能提前看到后续的词（即未来的词），否则会导致“作弊”，模型直接利用未来信息生成当前词。 如果不加以限制，解码器的自注意力机制会允许每个位置的词看到整个序列（包括未来词），从而破坏训练目标。

为了解决上述问题，在训练 解码器的时候使用了 掩码多头自注意力机制，通过掩码（mask）限制解码器只能关注当前词及其之前的词，屏蔽掉未来的信息。

掩码的作用

• 在计算注意力分数时，对未来的词（即目标序列中当前词右侧的词）施加一个负无穷大的权重，使得它们的注意力分数在 softmax 后变为 0。
• 这样，解码器只能利用当前词及其之前的上下文信息。

Cross Attention

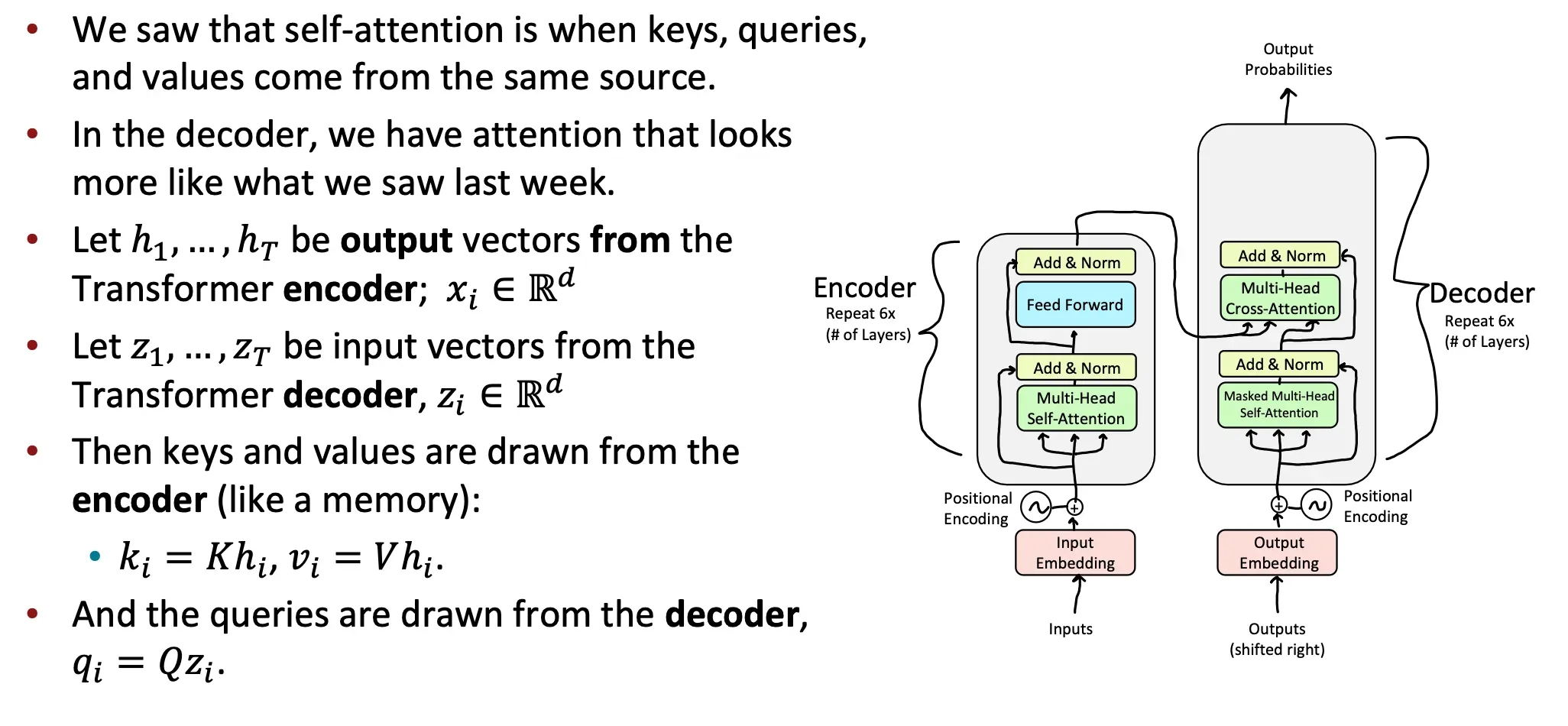
• 编码器输出 ( h_1, $\dots$, h_T )：编码器生成的上下文向量，表示输入序列的全局信息，供解码器使用。
• 解码器输入 ( z_1, $\dots$, z_T )：目标序列的嵌入表示，逐步生成目标序列。
• 键 (Key) 和 值 (Value)：从编码器的输出中计算得出，具体公式为：$$k_i=K{h}_i,v_i=V{h}_i$$
• 查询 (Query)：从解码器的当前状态中计算得出，公式为：$$q_i=Q{z}_i$$

最后：

Drawbacks and Variants of Transformers

问题：

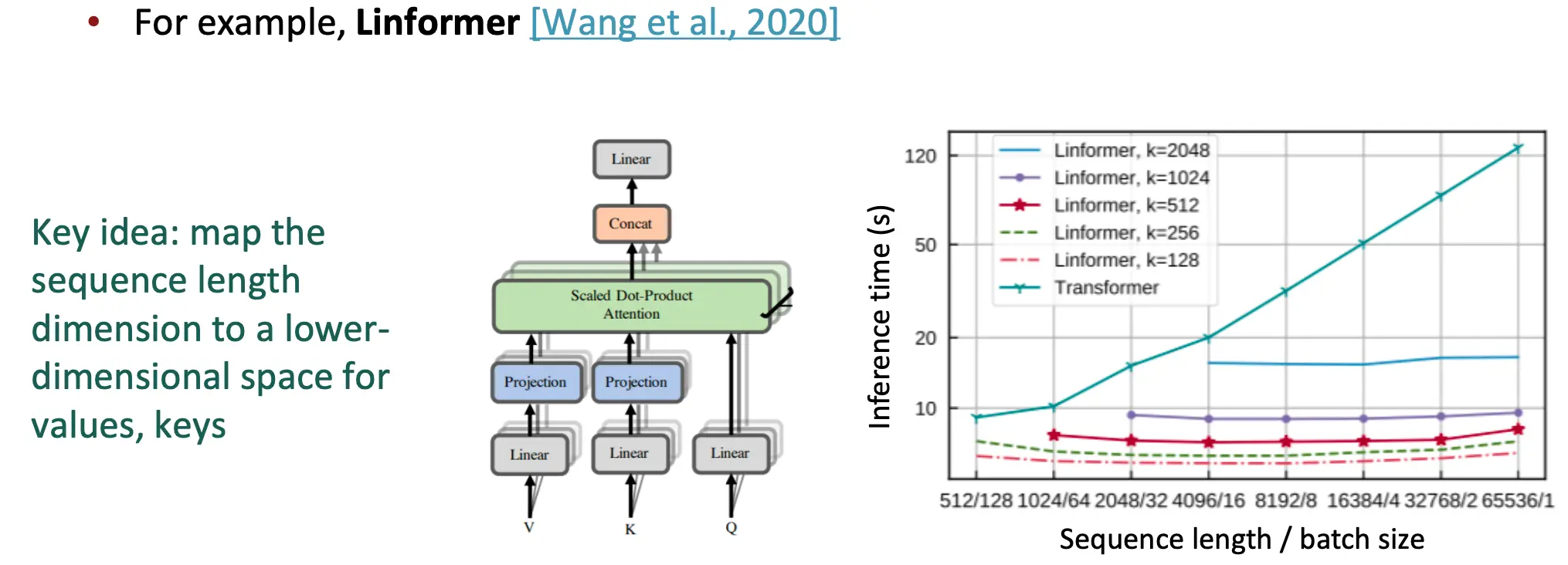
1. 自注意力中的二次计算：计算所有交互对意味着我们的计算随着序列长度呈二次增长！对于RNN，呈线性增长！ 最近已经有相当多的工作投入到这个问题中，我们能否构建像Transformer这样的模型，而不需要支付𝑂(𝑇^2)的全对自注意力成本？

• 随机注意力：
  每个位置随机选择一部分其他位置进行交互，而不是与所有位置交互。

• 窗口注意力：
  每个位置只与其局部窗口内的若干邻近位置交互（例如，前后 3-5 个位置）。

• 全局注意力：
  在稀疏连接的基础上，保留一些全局交互，例如让部分特殊位置（如句子的开头或结尾）与所有位置交互。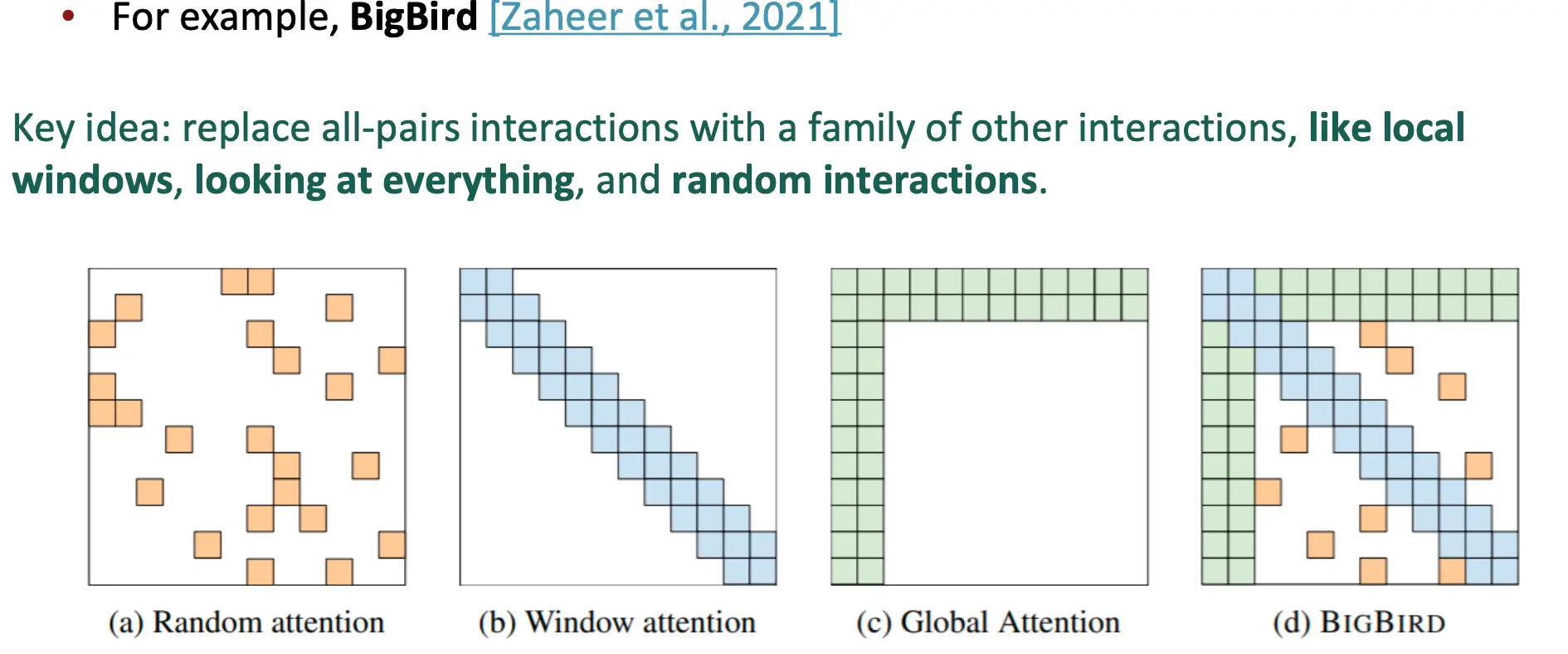

  

2. 位置编码，位置表示 然而没用，大多数对 Transformer 的改进在实际应用中并没有显著提升性能。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update