Regularisation

字数

2672 字

阅读时间

11 分钟

有两种方式去克服过拟合

• Regularisation：踩刹车
• Cross-Validation：检查底线

VC分析正则

对于VC分析，我们的初识结论是这样的： 在概率 1-sigma（置信度为sigma）的情况下，有：

$$E_{\mathrm{out}}(g)\le E_{\mathrm{in}}(g)+\mathrm{\Omega }(N,\mathcal{H},\delta ),\mathrm{\Omega }(N,\mathcal{H},\delta )=\sqrt{\frac{8}{N}\ln \frac{4m_{\mathcal{H}}(2N)}{\delta }}$$

而这里面一般N和sigma都是固定的，所以我们可以简化为：

$$E_{\mathrm{out}}(h)\le E_{\mathrm{in}}(h)+\mathrm{\Omega }(\mathcal{H}),$$

这里 $\mathrm{\Omega }(\mathcal{H})$ 相当于一个模型空间的惩罚项，模型空间太大（过于复杂），那么这玩意就会变大，Eout就大概率会烂掉

我们尝试让这个惩罚项 $\mathrm{\Omega }(\mathcal{H})$ 更收紧一点。 首先，我们假设 H9是9阶多项式，H2是2阶多项式，而目标函数g是一个2阶多项式。 我们去学习h，那么用一个更简单的h，h就更可能属于H2而不是H9，虽然H2也属于H9。 所以，

$$E_{\mathrm{out}}(h)\le E_{\mathrm{in}}(h)+\mathrm{\Omega }(\mathcal{H}),$$

这个式子也可以近似地看成：

$$\underset{h}{\mathrm{minimize}}{E}_{\mathrm{in}}(h)+\mathrm{\Omega }(h),$$

所以，我们的目标就是，限缩H的复杂度，尝试把H9限制到H2，来让学出来的h更简单。

三种正则

硬正则

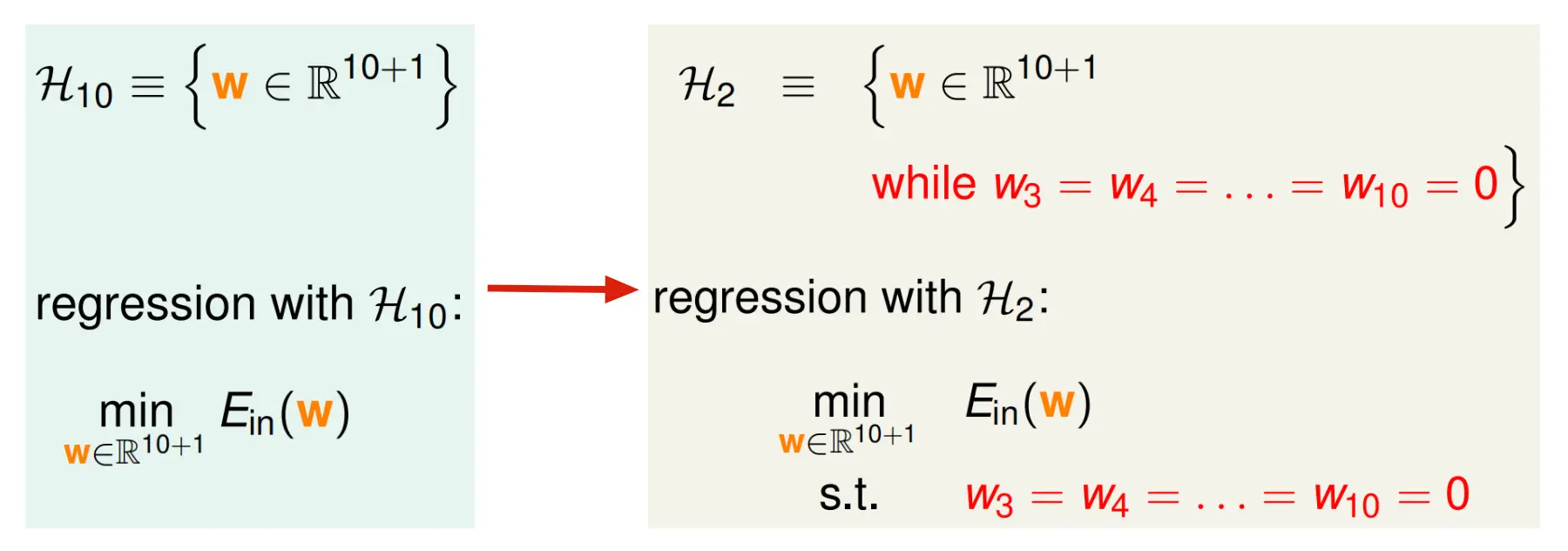限制3-10位的w必须为0.不仅限制了w数量，也限制了哪一位为0，比较僵硬

松正则 L0正则

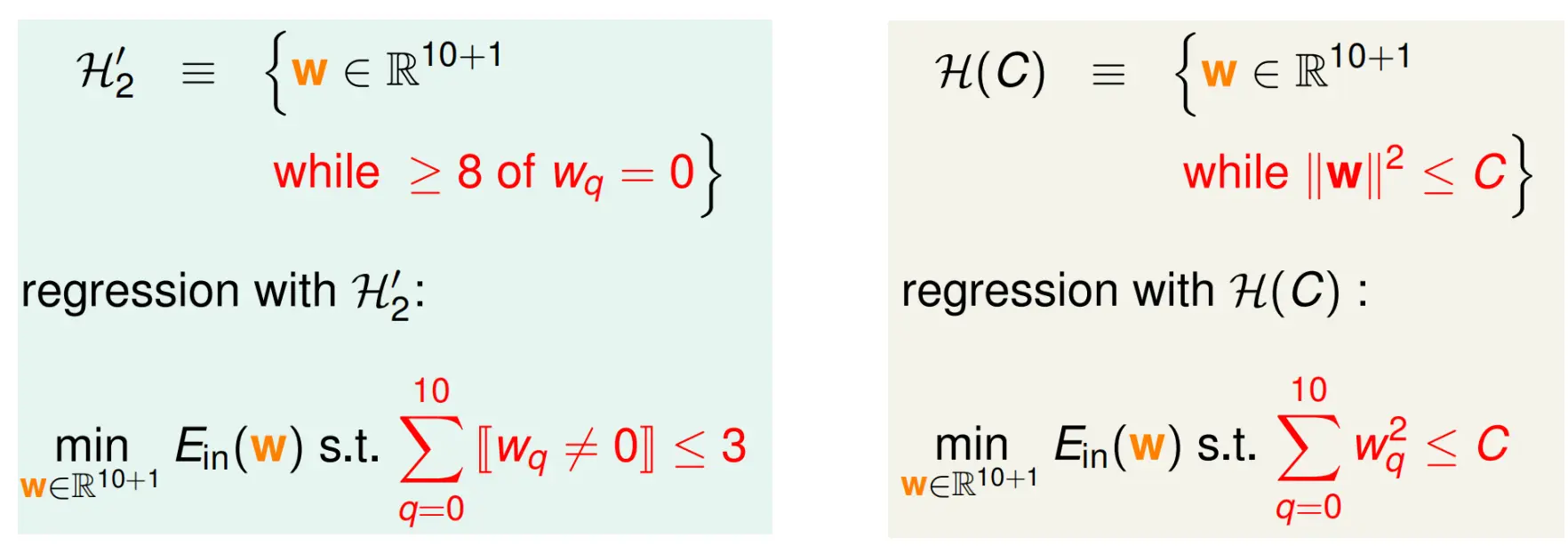
任意3位不为0就可以，只限制w数量，不限制w位置 属于NP-hard问题

软正则 L2正则

$\parallel w{\parallel }^2=\sum _{q=0}^{10}{w}_q^2$ 是参数的平方和。把参数平方和限制在C内，可以形成约束，模型不能“任性”地把系数调很大， 这个就是Ridge / L2 正则化

正则 in use

我们用线性回归来举例子 我们首先把 (X,y) 通过核函数映射为 (Z,y) 然后Ein就可以写成：

$$min:E_{\mathrm{in}}(\mathbf{w})=\frac{1}{N}\sum _{n=1}^N({\mathbf{w}}^{\mathrm{T}}{\mathbf{z}}_n-y_n{)}^2$$$$=\frac{1}{N}(Z\mathbf{w}-\mathbf{y}{)}^{\mathrm{T}}(Z\mathbf{w}-\mathbf{y})$$

那么最后w就可以表示为：

$${\mathbf{w}}_{\mathrm{lin}}=({\mathbb{Z}}^{\mathrm{T}}\mathbb{Z}{)}^{-1}{\mathbb{Z}}^{\mathrm{T}}\mathbf{y}$$

如果加上我们说的L2正则，那么我们的任务就变成了：

$$\begin{array}{rl}\underset{\mathbf{w}\in {\mathbb{R}}^{Q+1}}{min}& E_{\mathrm{in}}(\mathbf{w})=\frac{1}{N}\underset{(\mathrm{Zw}-\mathbf{y}{)}^T(\mathrm{Zw}-\mathbf{y})}{\underbrace{\sum _{n=1}^N({\mathbf{w}}^T{\mathbf{z}}_n-y_n{)}^2}}\\ \mathbf{s}\mathbf{.}\mathbf{t}\mathbf{.}& \underset{{\mathbf{w}}^T\mathbf{w}}{\underbrace{\sum _{q=0}^Q{w}_q^2}}\le c\end{array}$$

那么我们如何解决这种带约束的优化问题呢？采用拉格朗日乘子。

我们来结合几何图像来解释这个事情。

首先由于Ein可以写成：

$$E_{\mathrm{in}}(w)=\frac{1}{N}{(Zw-y)}^{\mathrm{\top }}(Zw-y)$$

这玩意经过数学变形后可以发现是一个正定二次型，画到坐标系里就是一个椭圆。 而正则项显然是个圆形。 蓝色箭头 $-\mathrm{\nabla }{E}_{\mathrm{in}}(w)$ 是让Ein下降最快的方向 而在红色的圆上，法线方向正好就是w本身。要在圆上找到使Ein最低的点，就要让下降方向正好“贴平”圆面。只有当两者平行时，沿球面内切线方向再无降低误差的可能，也就是说，让红色的线在蓝色方向没有分量即可。

接下来我们进行推导。我们把约束转化为拉格朗日松弛形式：

$$\mathcal{L}(w,\lambda )=E_{\mathrm{in}}(w)+\lambda (w^{\mathrm{\top }}w-C),\lambda \ge 0.$$

互补松弛w求偏导为0:

$$\mathrm{\nabla }{E}_{\mathrm{in}}(w_{\mathrm{REG}})+2\lambda w_{\mathrm{REG}}=0⟹\mathrm{\nabla }{E}_{\mathrm{in}}(w_{\mathrm{REG}})+\frac{2\lambda }{N}{w}_{\mathrm{REG}}=0$$

（如果把1/N吸收到lambda中，就是常见形式了） 从上面得到的最优条件，可以看出它等价于在目标中添加一个L2正则：

$$\underset{w}{min}{E}_{\mathrm{in}}(w)+\frac{2\lambda }{N}\frac{1}{2}\parallel w{\parallel }^2,$$

这就是典型的Ridge回归，lambda或者2lambda/N就是正则强度。

Augmented Error

我们把这个东西叫做Augmented Error：

$$E_{\mathrm{in}}(w)+\frac{2\lambda }{N}\frac{1}{2}\parallel w{\parallel }^2$$$$=\begin{array}{c}{E}_{\mathrm{in}}(w)\end{array}+\begin{array}{c}\frac{\lambda }{N}\end{array}{w}^{\mathrm{\top }}w.$$

我们在这里就不去算它的梯度下降了，直接求w梯度为0的解析解。：

$$\begin{array}{rl}\mathrm{\nabla }{E}_{\mathrm{aug}}(w)& =\mathrm{\nabla }\left[\begin{array}{c}{E}_{\mathrm{in}}(w)\end{array}\right]+\frac{\lambda }{N}\mathrm{\nabla }\left[\begin{array}{c}{w}^{\mathrm{\top }}w\end{array}\right]\\ & =\underset{\mathrm{\nabla }{E}_{\mathrm{in}}(w)}{\underbrace{\frac{2}{N}{Z}^{\mathrm{\top }}(Zw-y)}}+\frac{\lambda }{N}\left(2w\right)\\ & =\frac{2}{N}\left(Z^{\mathrm{\top }}Zw-Z^{\mathrm{\top }}y+\lambda w\right)\\ & =\frac{2}{N}[(Z^{\mathrm{\top }}Z+\lambda I)w-Z^{\mathrm{\top }}y]=0.\end{array}$$

解得：

$$(Z^{\mathrm{\top }}Z+\lambda I)w=Z^{\mathrm{\top }}y.$$

只要左边这玩意可逆，那么立刻可以看出：

$$w_{\mathrm{reg}}={(Z^{\mathrm{\top }}Z+\lambda I)}^{-1}{Z}^{\mathrm{\top }}y$$

当lambda为0的时候，可以看到就退回了无正则化的正常OLS解。 在这个过程中，lambda的选择是不太有解释性的。你需要用交叉验证选出使验证误差最小的那个。 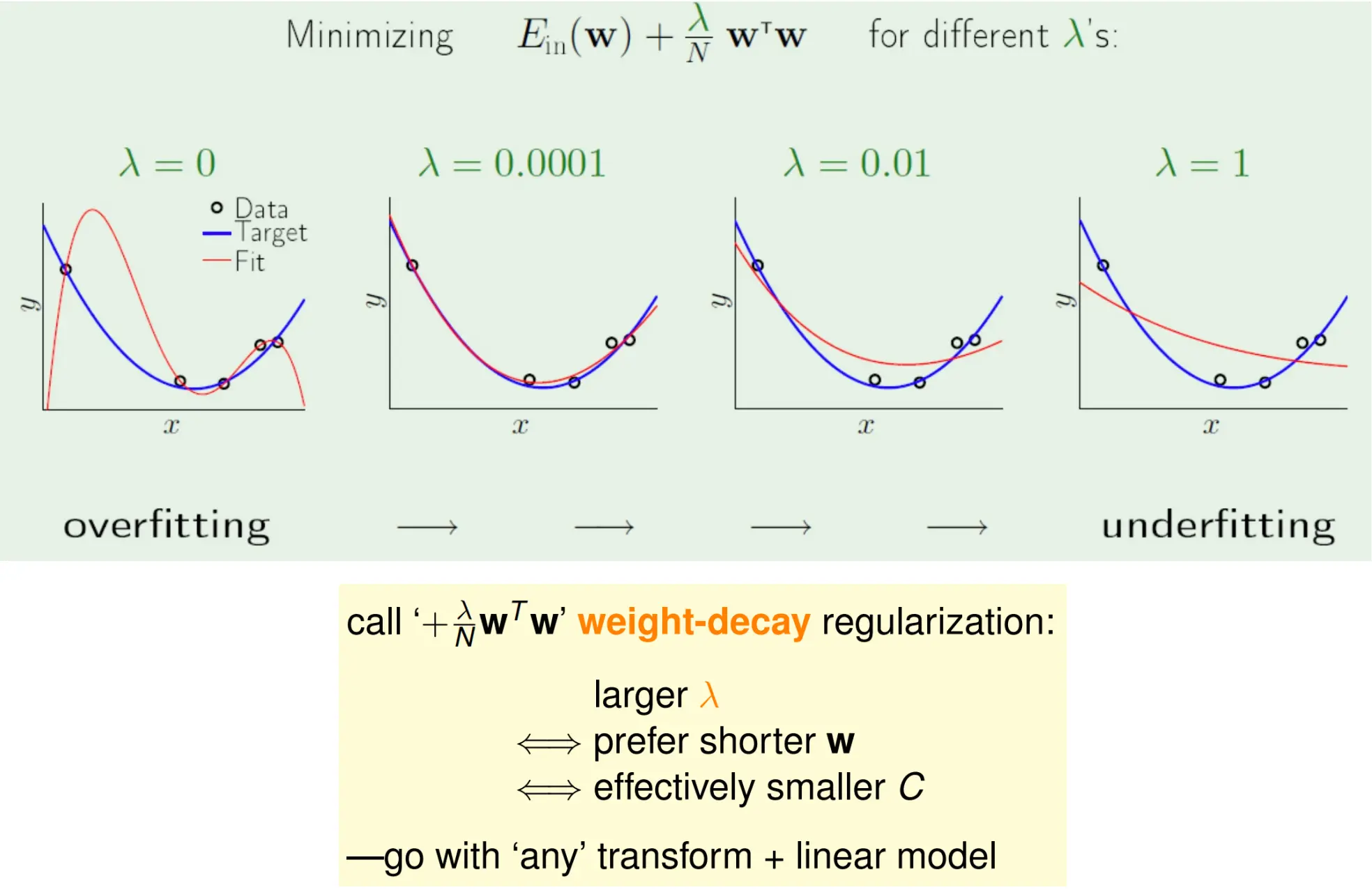L2正则又叫weight-decay正则，更大的lambda会倾向于学出更短的w。适用于任何transform + linear

L2正则与VC分析

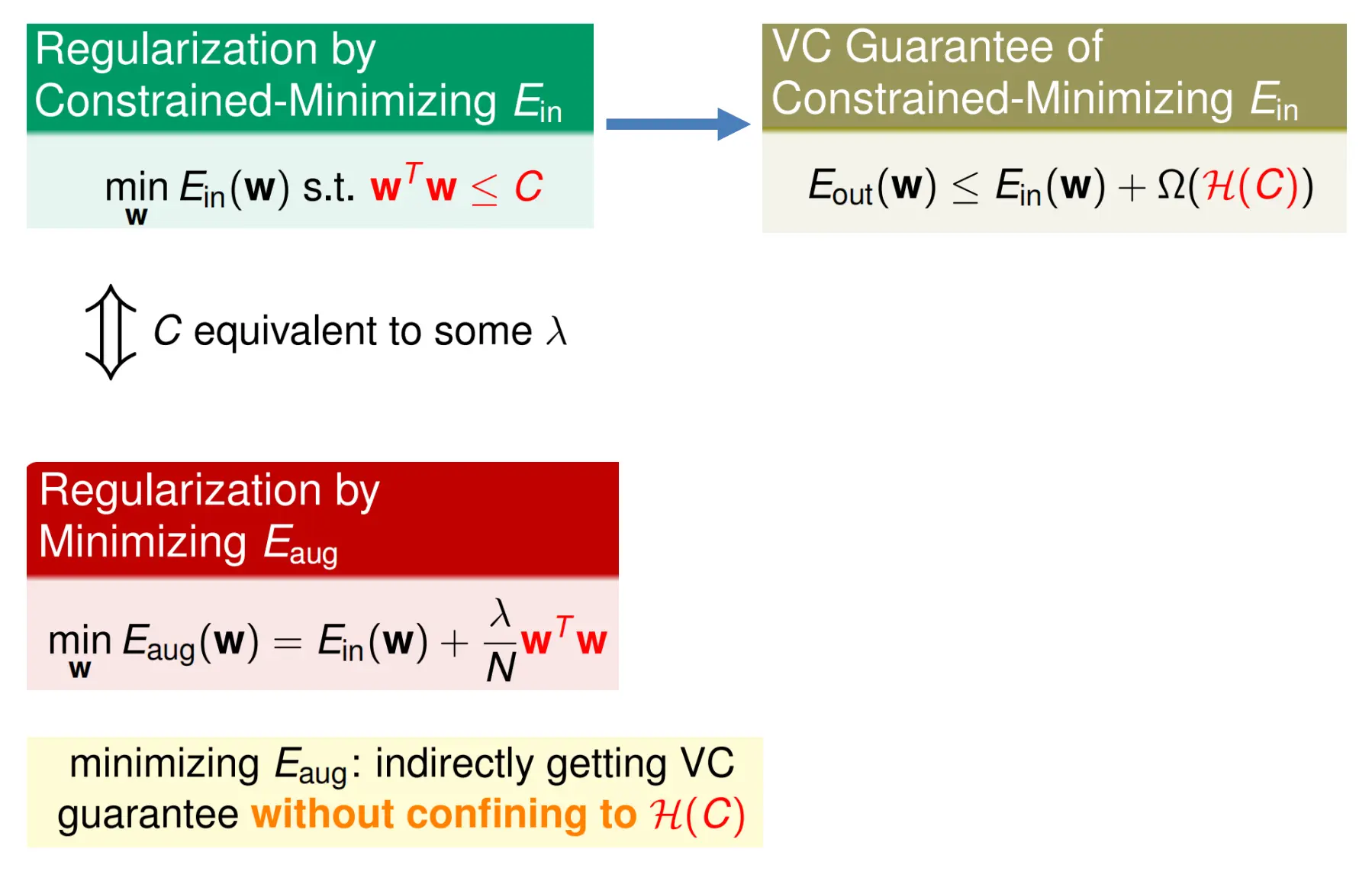绿色的，我们把模型的空间软切到了C内。 黄色的，当我们软切之后，VC告诉我们我们会自动获得一个上界 $E_{\mathrm{out}}(w)\le E_{\mathrm{in}}(w)+\mathrm{\Omega }(\mathcal{H}(C))$ 来控制泛化

而其实正则化强度lambda和C是存在等价关系的。我们原来是一个受限的优化问题：

$$\underset{w}{min}{E}_{\mathrm{in}}(w)\mathrm{s}.\mathrm{t}.\parallel w{\parallel }^2\le C.$$

我们使用拉格朗日乘子将其转化为了一个带惩罚的最小化问题：

$$\mathcal{L}(w,\mu )=E_{\mathrm{in}}(w)+\mu (\parallel w{\parallel }^2-C).$$

根据KKT条件我们有偏导为0:

$$\mathrm{\nabla }{E}_{\mathrm{in}}(w^{\ast })+\mu \cdot 2w^{\ast }=0.$$

等价于

$$\mathrm{\nabla }{E}_{\mathrm{in}}(w^{\ast })+\frac{2\lambda }{N}{w}^{\ast }=0,$$

存在某个映射C到lambda使得正则化既满足C又满足lambda。二者强对偶。

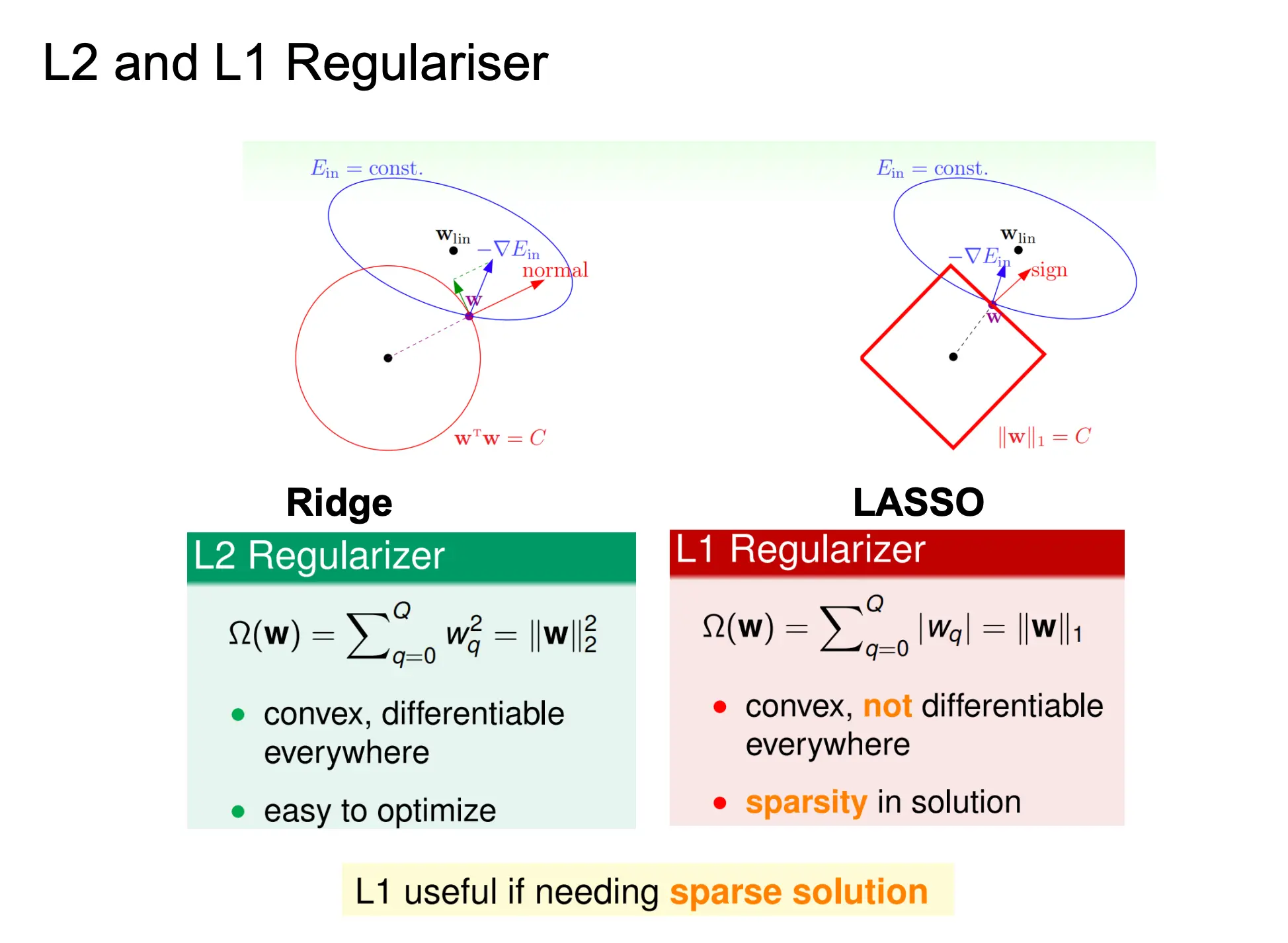
General正则

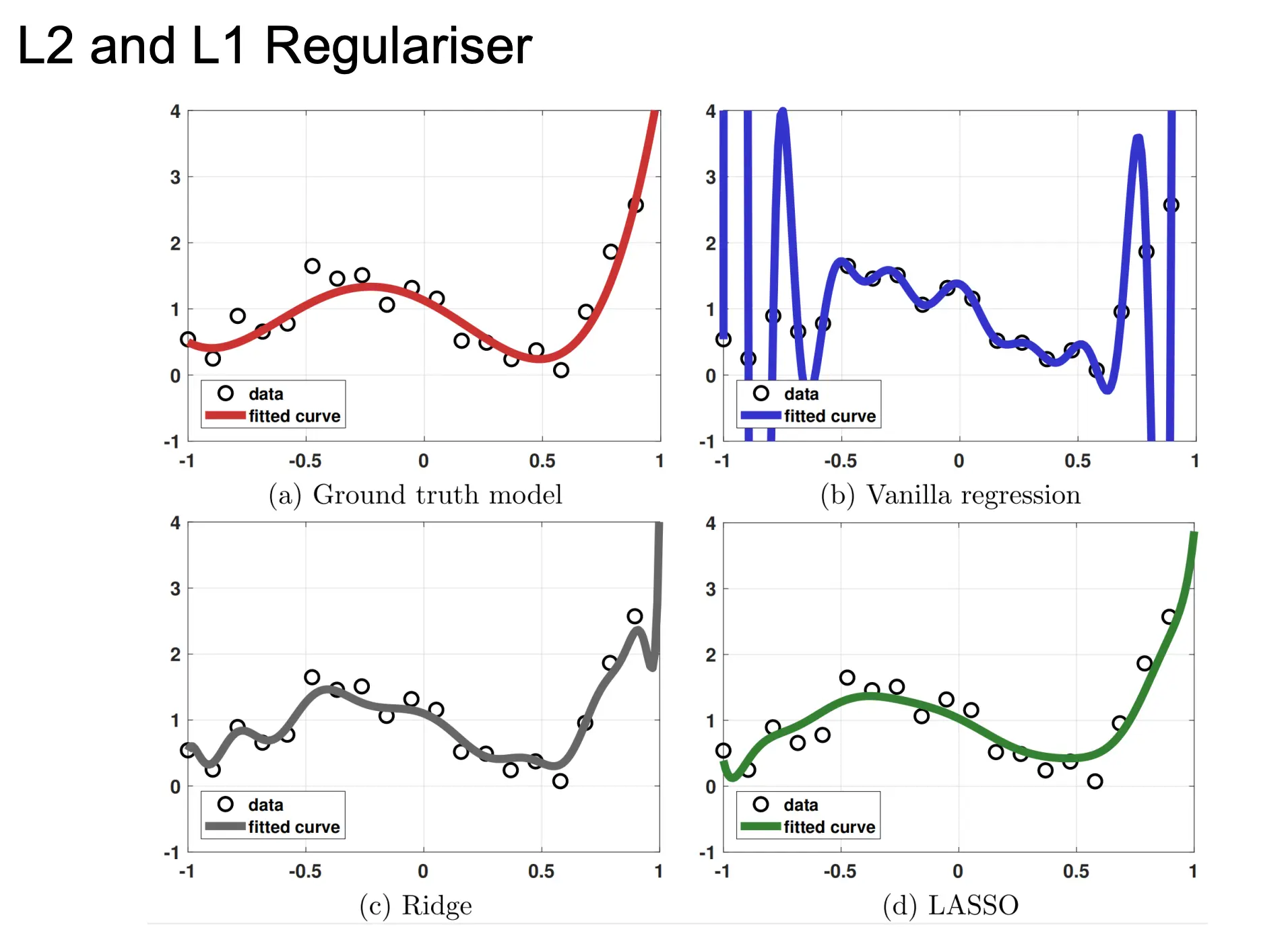
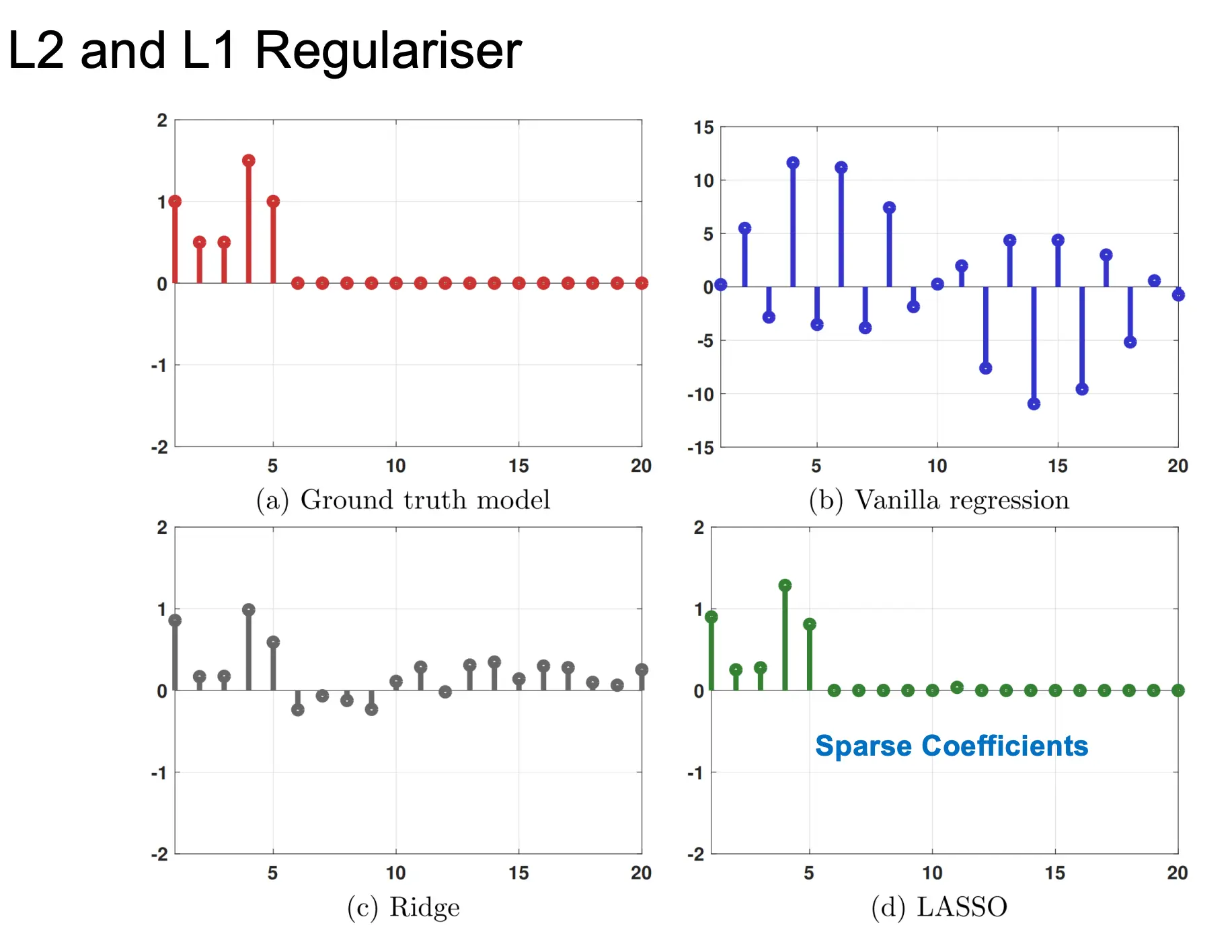
P=2就是L2正则（岭回归）。光滑的球面约束，能平滑地压缩所有权重。 P=1就是L1正则（LASSO），凸但不光滑的菱形等高面，会把一些权重恰好压到 0。得到一个稀疏解。 P<1是更激进的稀疏，等高面变得“更尖锐”，会比 L1 更猛烈地把绝大多数权重推向 0，得到更超稀疏的解。缺点是此时惩罚变得非凸，优化难度成倍增加（通常会陷入局部最优）。

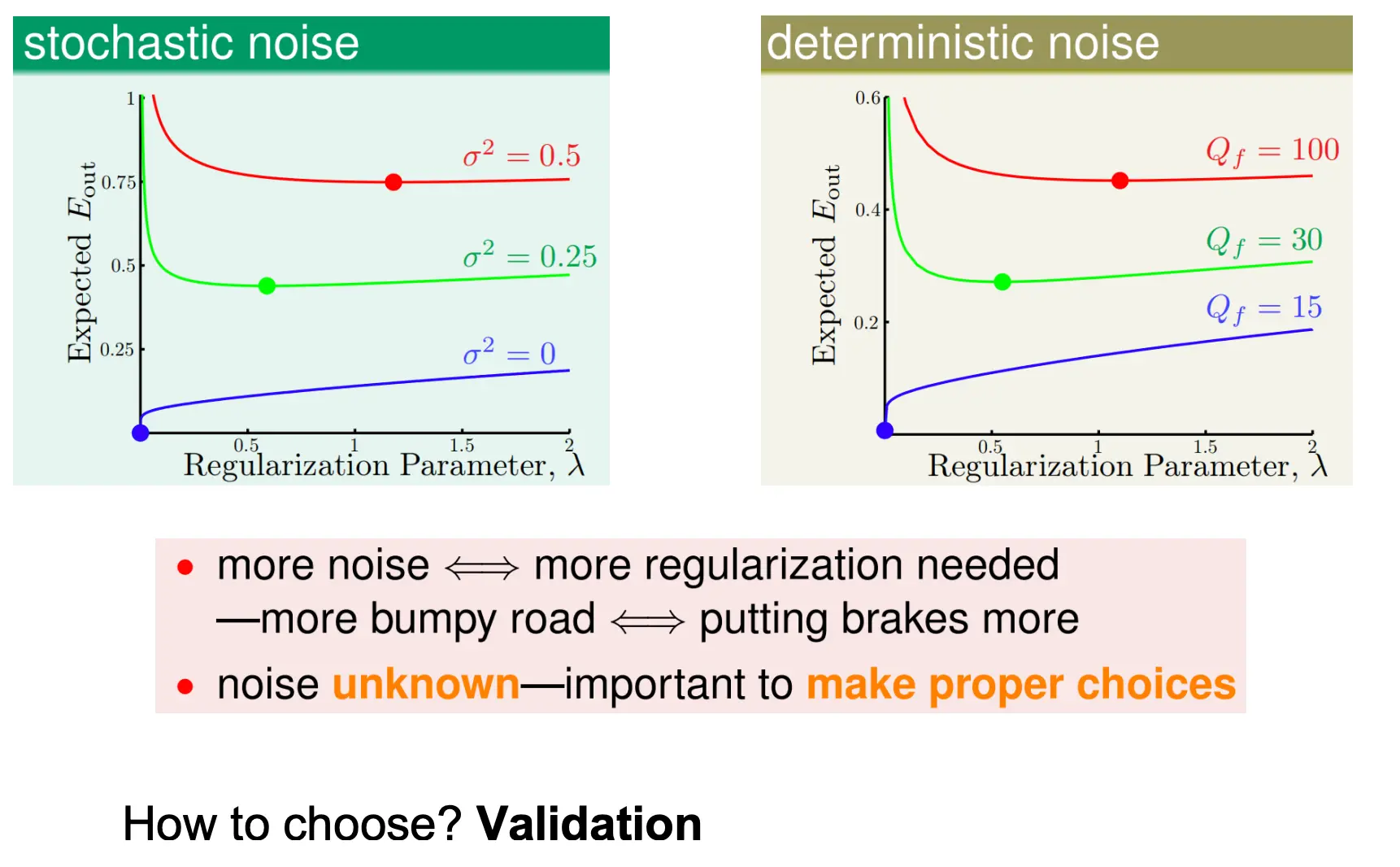对于随机噪声，噪声越大越需要大的正则强度。 对于确定性噪音（就是目标模型复杂度Q），高复杂度需要更大的正则强度 噪声水平未知，所以我们必须用 交叉验证（Validation） 去自动选出那个最能降低验证误差的lambda

贝叶斯视角的正则

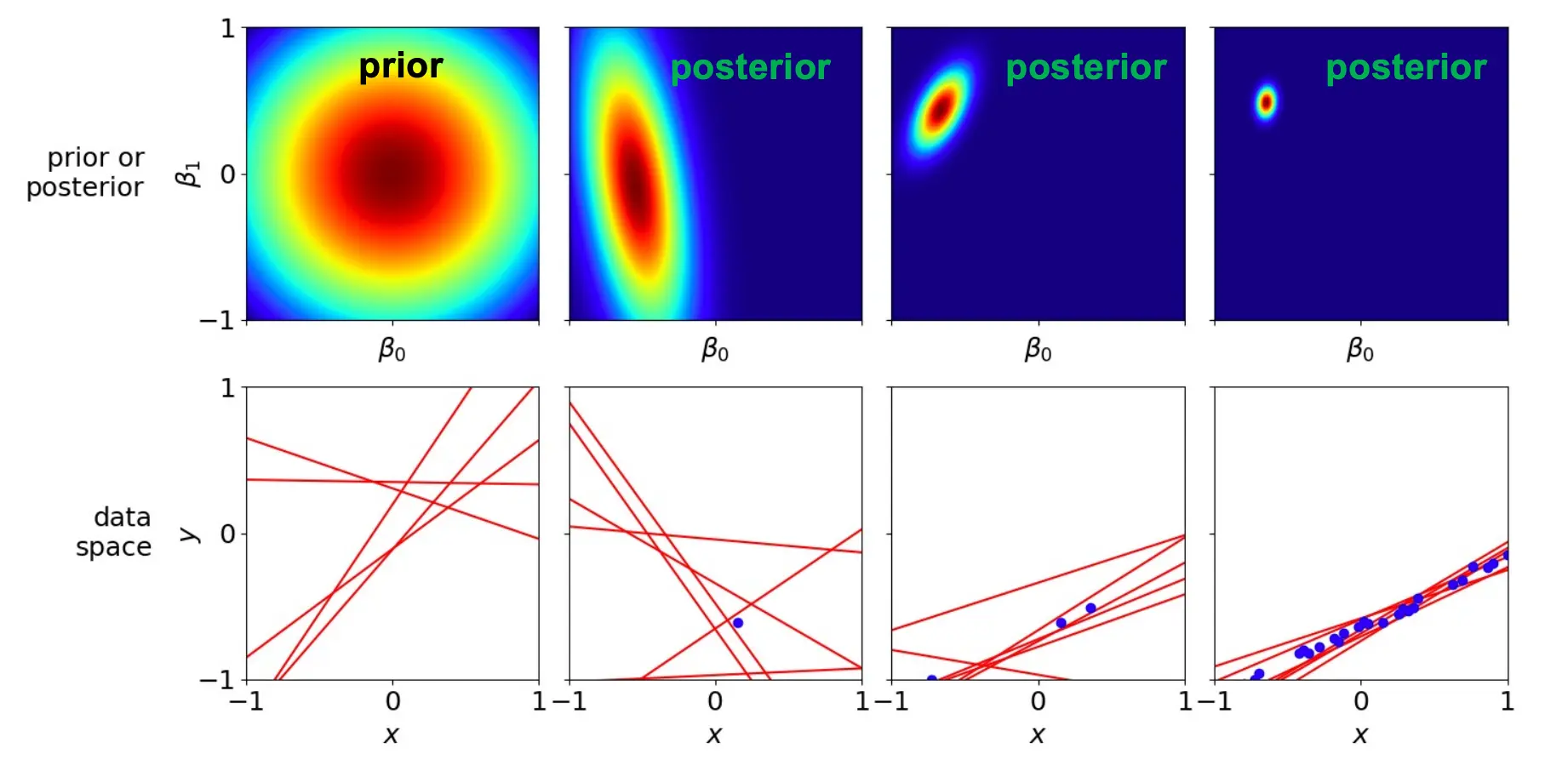先验是一个“橡皮筋”防止少量数据把参数拉得离谱，只有先验的时候对权重是没有偏好的。 后验宽窄直接反映了我们对权重的不确定程度

• 贝叶斯防过拟合：通过先验限制参数范围（相当于给参数加正则化），避免少量噪声把模型拟合得过弯。
• 先验是正则化器：在数据稀缺时“拉回”参数；在数据多时又会被似然主导，自动“松手”让模型自由拟合。
• 后验量化不确定性：后验分布越窄，我们越有信心这是“正确”参数；反之则说明数据或假设空间不足。

贝叶斯MAP

对于贝叶斯，完整的预测是从后验中采样几组w，然后把这些曲线在新输入点上的预测值求平均。 然而，对于高维的w来说，后验采样本身就很昂贵。所以我们推出MAP (Maximum a posteriori)，后验模式点估计

核心思想有点像极大似然法，用概率最大者替代最优解：

$$w_{\mathrm{MAP}}=\arg \underset{w}{max}p(w\mid \mathcal{D})⟺\arg \underset{w}{min}[-\log p(\mathcal{D}\mid w)-\log p(w)],$$

在 Gaussian–linear 的情况下，这恰好等价于我们之前导出的 Ridge 解（或说是后验分布的均值）。

MAP情况下贝叶斯估计与L2岭回归解析式相同

我们用贝叶斯语言再来审视一遍线性回归 首先我们有N个观测 假设输出是一个带有高斯噪音的线性模型：

$$y_i=\underset{\hat{y}(x_i,\omega )}{\underbrace{{\omega }^{\mathsf{T}}\varphi (x_i)}}+{ϵ}_i,{ϵ}_i\sim \mathcal{N}(0,{\beta }^{-1}).$$

那么似然函数就是：

$$p(y\mid X,\omega ,\beta )=\prod _{i=1}^N\mathcal{N}(y_i\mid {\omega }^{\mathsf{T}}\varphi (x_i),{\beta }^{-1}).$$

看到数据前我们有一个先验：

$$p(\omega )=\mathcal{N}(\omega \mid 0,{\alpha }^{-1}I).$$

按照贝叶斯公式：

$$p(\omega \mid y,X)\propto p(y\mid X,\omega )p(\omega ).$$

把两个高斯相乘，取指数，等号右边就变成了：

$$\exp \{-\frac{\beta }{2}\sum _{i=1}^N{(y_i-{\omega }^{\mathrm{\top }}\varphi (x_i))}^2-\frac{\alpha }{2}{\omega }^{\mathrm{\top }}\omega \}.$$

最后那一项看起来就是L2正则。 接下来用MAP点估计：

$${\omega }_{\mathrm{MAP}}=\arg \underset{\omega }{max}p(\omega \mid y,X)=\arg \underset{\omega }{min}[\frac{\beta }{2}\sum _i(y_i-{\omega }^{\mathrm{\top }}\varphi (x_i){)}^2+\frac{\alpha }{2}{\omega }^{\mathrm{\top }}\omega ].$$

于是 MAP 解 等价 于我们用 L2 正则化做线性回归时得到的解析解。

我们来看一下不带L2的MLE以及MAP的例子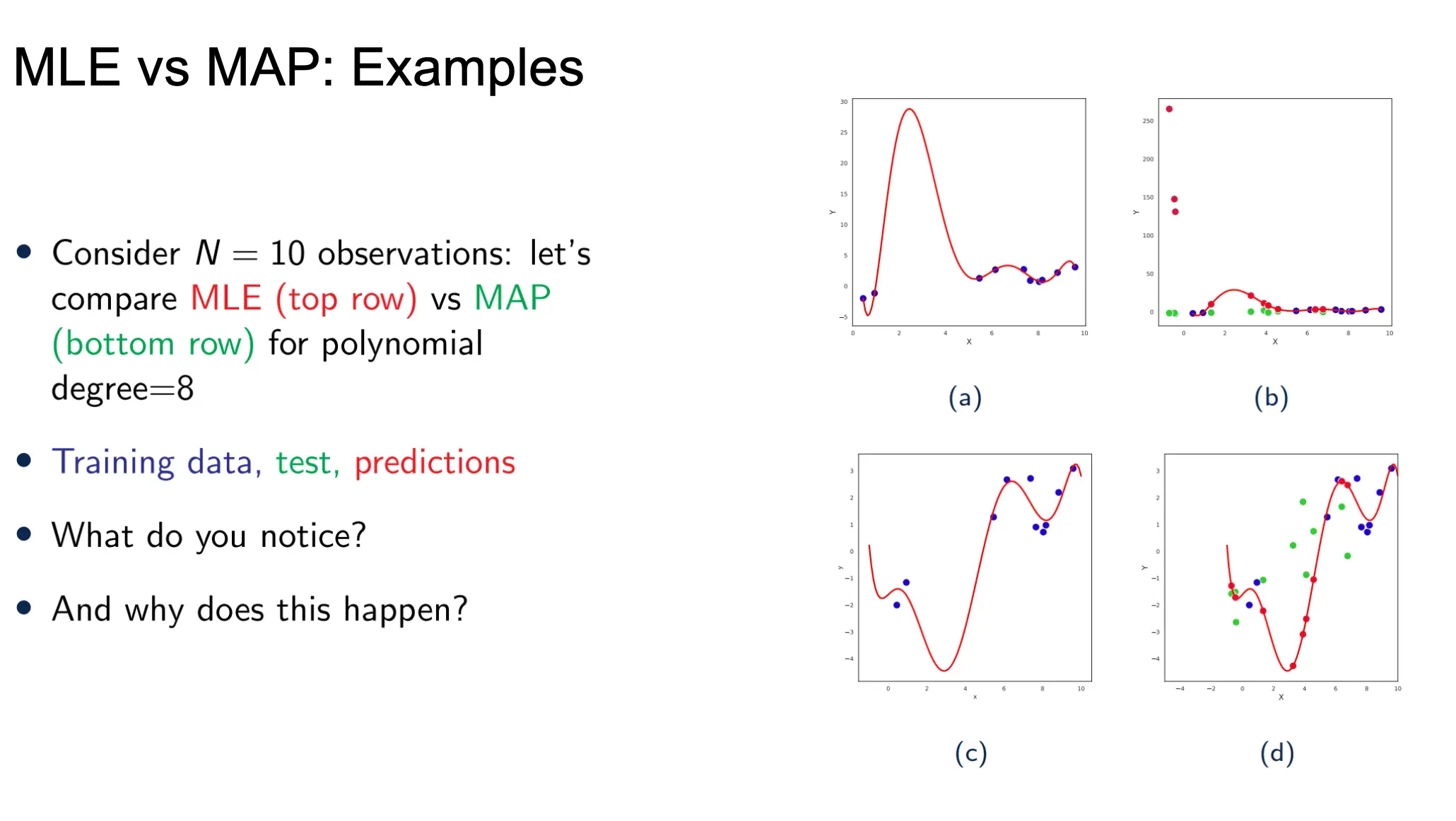： 可以看到，当（a）数据比较干净的情况下，b中无正则MLE与有正则MAP差不多 但当c这种离群点比较多的情况下，不带正则的MLE在训练点覆盖不到的区域，预测完全是多项式的任性外推，很容易偏离真实趋势。 而带正则的MAP 先验让模型“往零靠”——在训练覆盖不到的地方曲线更平直——因而通常能提供更合理的外推。

• 如果你只关心拟合精度、数据量充足、噪声又不极端，MLE（或 MAP 都差不多）就足够。
• 如果你在意鲁棒性、离群点多、样本稀疏、需要合理地外推到没见过的输入，带先验的 MAP／L2 正则化往往会给出更稳健的结果。

Takeaway Message

• 凡是训练模型，都试试加正则化
• 有噪声、样本少、目标太复杂时特别管用
• 只要 λ（正则强度）选得合适，收益往往大于风险
• 在现代深度学习里，更是随手可用
  • 权重衰减（Weight Decay）：L2 正则
  • L1 稀疏化：让部分神经元连接权重变为零，便于压缩/剪枝。
  • Dropout、BatchNorm、早停 等也可看作结构化的正则化手段。

总结

• MLE = OLS
• MAP = L2 正则化回归
• 高斯先验 ⇒ 二次正则项
• MAP 下的“二次惩罚”源自 $\ln p(w)\propto -\parallel w{\parallel }^2$ ，它会收缩（shrink）权重向量，使模型不至于随意挖掘噪声而过度弯折，从而减少过拟合。
• L1 正则：LASSO
  • 如果把先验换成 拉普拉斯分布（Laplace），其对数正好给出L1正则
  • 这就是 LASSO 正则化，它不仅收缩权重，还能把部分权重压成零，生成稀疏解，方便特征选择。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update