SR锁存
 SR为11未定义
SR为11未定义
D锁存
 clk为1时D与Q透明,为0时保存状态
clk为1时D与Q透明,为0时保存状态
D触发
 只在上升沿触发
只在上升沿触发
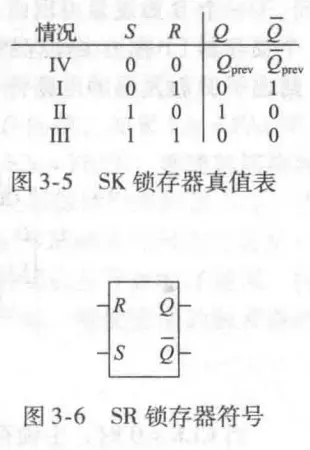
寄存器
带使能端的触发器

复位触发器

多路复用器
从结果来看,IBGA在所有数据集上获得了最优解,满足所有约束条件且成本最低。BGA排名第二,在小数据集(sppnw41)上实现了Violation = 0,但在更大的问题(sppnw42、43)上,它难以完全覆盖所有行,导致Violation和Cost高于IBGA。
使用锦标赛选择的BGA结果略优于使用截断排名。我认为这是因为锦标赛选择更好地模拟了自然环境中的竞争条件,在那里你不需要与世界上的每个人竞争,只需要击败你周围的几个竞争对手。SA的解决方案质量最差。
IBGA的优势主要来自三个方面:伪随机初始化提供了更好的初始种群,为搜索提供了更好的起点。启发式修复算子积极修复违反约束的解决方案,平衡成本和覆盖范围。随机排名打破了固定的选择顺序,增加了搜索的多样性,避免了过早收敛。这些改进使IBGA能够在所有测试数据上找到最优解。
从解的质量来看,IBGA > BGA > SA。IBGA在所有数据集上都达到了相对最优的解,满足violation且成本最低。伪随机初始化提供了一个好的搜索起点,实际上这个方法提供的起点甚至好过BGA,SA的搜索终点。启发式修复算子可以修复违反约束的解,而随机排名为排名引入了随机性,增加了搜索的多样性,这些改进让IBGA比剩下的方法更好。 对于BGA来说,使用锦标赛选择的BGA略优于使用截断排名。我认为这是因为锦标赛选择模拟了自然环境,即你不需要打败所有人,如果想要繁衍后代,你只需要击败你周围的人即可。SA的解质量最差,这符合预期。
从图\ref{fig:curve}可以观察到收敛速度。IBGA以最快的速度收敛到最优解,其次是BGA,而SA最慢且波动较大。IBGA的优势在于伪随机初始化提供了高质量的起始点,使其在第一代就获得了良好的解质量,甚至比SA的最终搜索结果更好。启发式修复算子可以快速修正违反约束的解,迅速将违反降至0。
BGA缺乏伪随机初始化,初始解质量较低,需要更多迭代进行优化,但仍然比SA快。SA仅依赖于邻域搜索,缺乏种群进化的优势,导致收敛缓慢且解质量不稳定。IBGA在所有测试数据上稳定收敛到相同的最优解,而BGA可能会陷入不同的局部最优解。SA的结果存在较大差异。
在BGA中,使用截断排序时的收敛速度略快于使用锦标赛选择时。我认为这是因为截断排序施加了比锦标赛选择更大的选择压力,导致更快的收敛但更容易陷入局部最小值。这也解释了为什么其结果略逊于锦标赛选择的结果。
从图\ref{fig:curve}可以看到方法的收敛速度。收敛速度来看,IBGA > BGA > SA。并且SA的波动更大。上面已经提到,伪随机初始化提供了甚至比BGA和SA搜索终点更优的搜索起点,另外,启发式改进算子可以快速修正违反了violation的解,让violation快速降到0.
BGA初始解的质量低,所以需要多个generation进行优化。但是还是要比SA快,因为SA只依赖于邻域搜索,且是个体搜索,没有BGA中种群进化的优势。
BGA使用截断排序的收敛速度快于锦标赛选择。我认为这是因为截断排序对种群的选择压力更大,导致了收敛更快。但选择压力大也导致了其容易陷入局部最优,这也是导致其结果质量差于锦标赛选择的原因。
SA具有最短的单次搜索时间,BGA处于中间位置,而IBGA则是最长的。然而,就整体收敛时间而言,IBGA实际上是最快的。SA只维持一个解决方案,并且具有最低的计算成本,但它收敛非常缓慢,整体优化时间更长。BGA受益于种群进化,因此单次计算成本高于SA,但由于收敛更快,整体优化时间更好。IBGA虽然由于额外的启发式修复和随机排名而具有最高的单次计算成本,但由于其快速收敛,整体优化时间最短。总的来说,IBGA是最佳选择。
如果只讨论单次搜索时间,而不讨论整体搜索时间,那么T(SA) < T(BGA) < T(IBGA)。这很好解释,SA只在一个个体上进行搜索,计算成本最低,但收敛更慢,整体优化时间更长。BGA和IBGA使用种群进化,所以单次计算成本更高。而IBGA由于使用了更复杂的算子,所以计算成本最高。但由于IBGA算子的高效性,使得算法的单词计算成本高的缺点被算法效率高所覆盖,所以IBGA整体优化时间最短。总的来说,IBGA是最优的算法。
\item \textbf{优化目标:} 这两种方法的目标都是平衡解决方案的可行性和质量,避免在适应度函数中过度或不足地惩罚。这样可以避免过早收敛到局部最小值或偏离可行区域。
这两种方法都试图平衡解的violation和cost,而避免手动设置惩罚权重的过惩罚与欠惩罚。这样可以避免过早收敛到局部最优或者偏离最优方向。
两种方法都同时考虑成本函数和惩罚函数,允许一定数量的不可行解决方案存在。这有助于保持搜索多样性并保留潜在有希望的解决方案。
这两种方法都同时考虑cost和violation,允许部分不可行解存在在种群中,保持了搜索的多样性。
排名替换是一种确定性方法,它将解决方案分为四个子组,并按照预定义的顺序检查个体。相比之下,随机排名根据概率
排名替换是确定性算法,把种群分成四个子组,并按照预先定义好的顺序来检查每个个体。随机排名以概率p使用cost function进行比较,以1-p概率使用violation函数比较解,通过超参数p引入了随机性。
随机排名仅为解决方案提供排名,而不指定如何选择下一代个体。排名替换是一种完整的选择机制,明确规定了在进化过程中个体如何保留或丢弃。
随机排名只是提供了种群的排名,至于如何保留下一代个体由选择方法决定。排名替换提供了一套完整的排名与选择方法,明确了如何排序,如何选择。
标准二进制遗传算法是一种进化算法,其基因型使用二进制编码。由于未指定选择算子,我实现了两种变体:截断选择和锦标赛选择。BGA的流程图如图\ref{fig:bgaflow}所示。我将使用流程图解释算法。
首先,我们运行初始化算法\texttt{population_size}次,生成初始种群。这种初始化方法与模拟退火中使用的方法相同。接下来,我们进入循环。我们根据种群中的适应度计算结果选择父代,然后使用交叉和突变算子生成后代。然后,重新计算种群及其后代的适应度,对所有个体进行排名,选择排名靠前的\texttt{population_size}个个体组成新种群。重复此过程,直到达到最大迭代次数或满足其他终止条件。最后,种群中适应度最好的个体即为搜索结果。
对于截断选择,根据适应度对种群中的个体进行排序,选择排名靠前的\texttt{population_size}个个体作为父代。对于锦标赛选择,每次从种群中随机抽取\texttt{k}个个体,选择适应度最好的个体作为父代。
Standard binary genetic algorithm是进化算法,通过种群进化,genotype用二进制编码。由于要求里并未指定选择算子,我实现了截断选择和锦标赛选择两个版本。BGA的流程图如图\ref{fig:bgaflow}所示。
我们首先用初始化算法生成population_size大小的初始种群,然后进入循环,根据fitness的计算结果来选择父代,用交叉和突变产生后代,重新计算种群以及后代fitness后,对种群排名,选择前population_size个个体作为新种群,不断重复,直到满足终止条件或者达到最大迭代次数。
改进的BGA(IBGA)是指一种BGA算法,该算法使用伪随机初始化方法\cite{chu1998constraint}进行初始种群生成,使用随机排名方法\cite{runarsson2000stochastic}进行排序,并使用启发式改进算子\cite{chu1998constraint}修复生成的后代。由于算法框架与BGA大致相同,我将重点关注这三个算子。由于详细的伪代码已在先前的论文中提供,我将提供一个简化且易于理解的伪代码版本供参考。IBGA的伪代码如算法\ref{alg:ibga}所示,流程图如图\ref{fig:ibgaflow}所示。
改进的BGA(IBGA)使用伪随机初始化方法\cite{chu1998constraint},随机排名方法\cite{runarsson2000stochastic}以及启发式改进算子\cite{chu1998constraint}对初始BGA的算子进行替换。对于每个算子的伪代码,由于提供的论文里已经有了详细的伪代码,我认为直接复制过来无法体现我的理解,所以我用一种易于理解的伪代码进行了算法的描述。流程图如图\ref{fig:ibgaflow}所示。
矩阵
在这个算子中,构建alpha_i矩阵十分关键,它用于检索可以覆盖第i行的列j。这是本算法能够快速实现的基础。本算法的主要思想是选择一个未被覆盖的行i,然后选择一个可以覆盖行i但不过覆盖其他列已经覆盖的行的列j。重复这个过程,知道找不到这样的列为止。因为i和j的选择具有随机性,所以这个算子也是个随机算法。该方法的伪代码是算法 \ref{alg:pseudo_random_init},流程图是图 \ref{fig:psudoinitflow}。
这个算法类似于改进版的冒泡排序。这种方法的思想是为了防止过度和不足的惩罚,排名个体时需要同时考虑成本函数和惩罚函数。具体来说,如果两者都不违反约束条件,则直接比较成本函数。否则,根据概率 p 比较成本函数,根据概率 1-p 比较惩罚函数以获得排名。p 和迭代次数是超参数。该方法的伪代码是算法 \ref{alg:stochastic_ranking},流程图是图 \ref{fig:strflow}。
这个算子讲座已经讲过了,类似于一个冒泡排序。但我认为它像哪种排序方法并不重要,这里面最重要的思想是,它重新定义了两个个体如何比较,也就是定义了二者的偏序关系。只要有了这个比较关系,我认为使用什么排序方法都可以。这种方法在两个个体都不违反violation的时候直接比较cost function。否则,就以概率p比较成本函数,以概率1-p比较violation函数。p和迭代次数都属于超参数。该方法的伪代码是算法 \ref{alg:stochastic_ranking},流程图是图 \ref{fig:strflow}。
这个操作符旨在修复由变异和交叉生成的后代解决方案,这些解决方案违反了太多约束,导致质量不佳、覆盖不足或覆盖过度。核心思想是通过DROP和ADD过程防止覆盖过度和覆盖不足。
对于给定的后代解决方案,将随机选择一个已覆盖的列进行检查。如果它覆盖的任何行都被覆盖过度,则删除该列。这是DROP过程。由于DROP可能引入额外的覆盖不足,因此接下来是ADD过程。
对于所有未覆盖的行,算法尝试从可用的列中找到一组列,这些列仅覆盖当前未覆盖的行。它使用基于比率(\frac{\text{成本}}{\text{覆盖行数}})的贪婪策略选择一列,并将其添加到解决方案中。因此,最终解决方案要么确保每行仅被覆盖一次,要么保持覆盖不足,但永远不会覆盖过度。此方法的伪代码为Algorithm \ref{alg:heuristic_improvement},流程图为Figure \ref{fig:repairflow}。
这个算子的想法其实很符合直觉,但用严格算法语言描述起来十分麻烦。它的作用是通过DROP和ADD过程来防止过度覆盖或欠覆盖。
对于已经给定的解,DROP过程是,随机选择一个已经被覆盖的列检查,如果它被覆盖超过一次,那么就删除这个列。ADD过程是,统计所有未覆盖过的行,算法尝试找出仅覆盖未被覆盖的行的列。如果有多个满足要求的列,就基于比率(\frac{\text{cost}}{\text{num of coverd}}) 这一贪心策略来选择一列,并将其加到解中。最后解的结构就是,要么每行只被覆盖过一次,要么就没被覆盖,绝对不会被多次覆盖。此方法的伪代码为Algorithm \ref{alg:heuristic_improvement},流程图为Figure \ref{fig:repairflow}。
 Larry Shi
Larry Shi