Week 8 Co-Evolution

字数

3364 字

阅读时间

14 分钟

Co-Evolution 定义

互相作用的物种之间，由于彼此施加的自然选择压力而发生的互惠式基因改变。

一朵花可能会进化出特定形状的花瓣来吸引特定的蝴蝶；同时，蝴蝶的口器也可能随之进化得更适合采集这种花的花蜜。

对抗搜索

概念很容易理解，在环境y下找到最优的x，也就是说，在环境y最差的情况下，给出最好的选择x，从而得到最优的结果。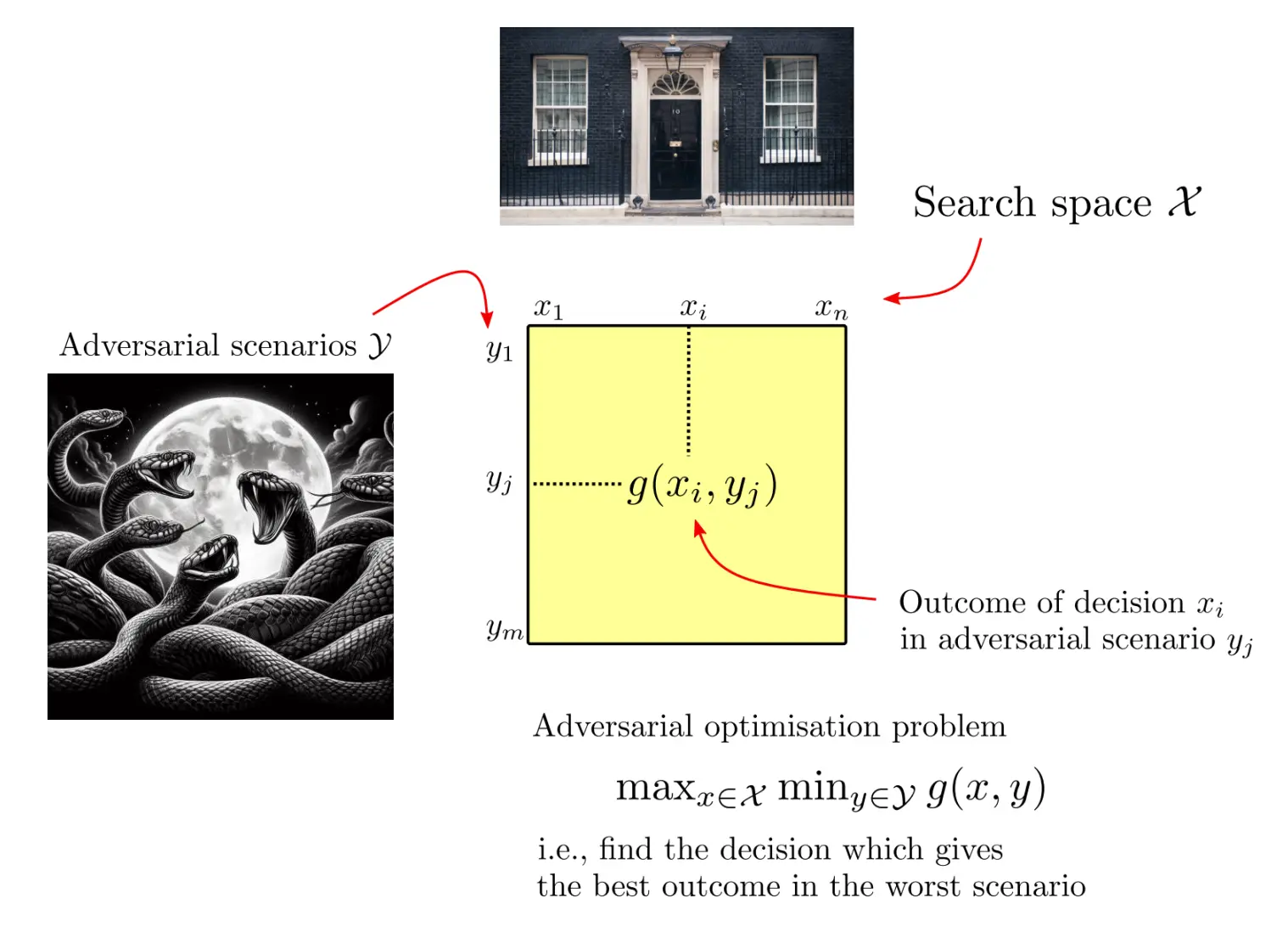

一个典型的例子如图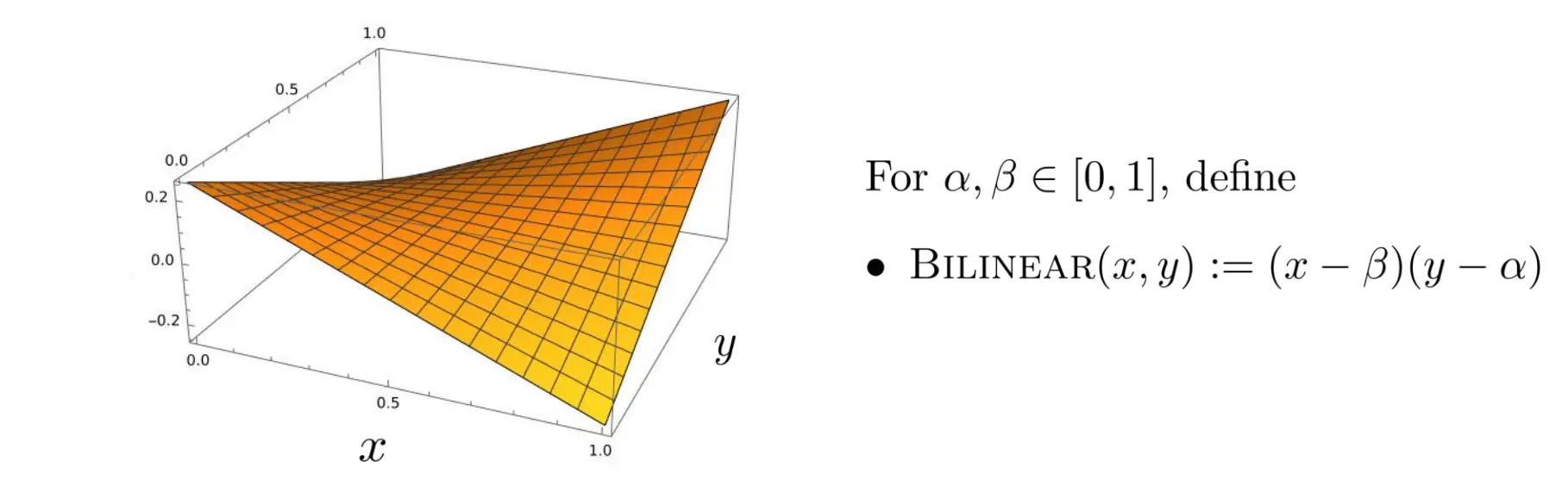： alpha和beta都是固定参数，而x和y是玩家的策略。 玩家x是捕食者，希望最大化收益，而y是猎物，希望最小化收益，这就构成了一个minmax问题：

$$\underset{x}{max}\underset{y}{min}(x-\beta )(y-\alpha )$$

这就像是个纳什均衡问题。当x为beta，y为alpha时达到鞍点，也就是说，无论猎物y怎么选，x只要选beta，那么x的收益最高。同理，无论x猎食者怎么选，y只要选了alpha，那么就是最优。所以x为beta，y为alpha就是一个平衡点，纳什均衡，鞍点。

Co-Evolution算法

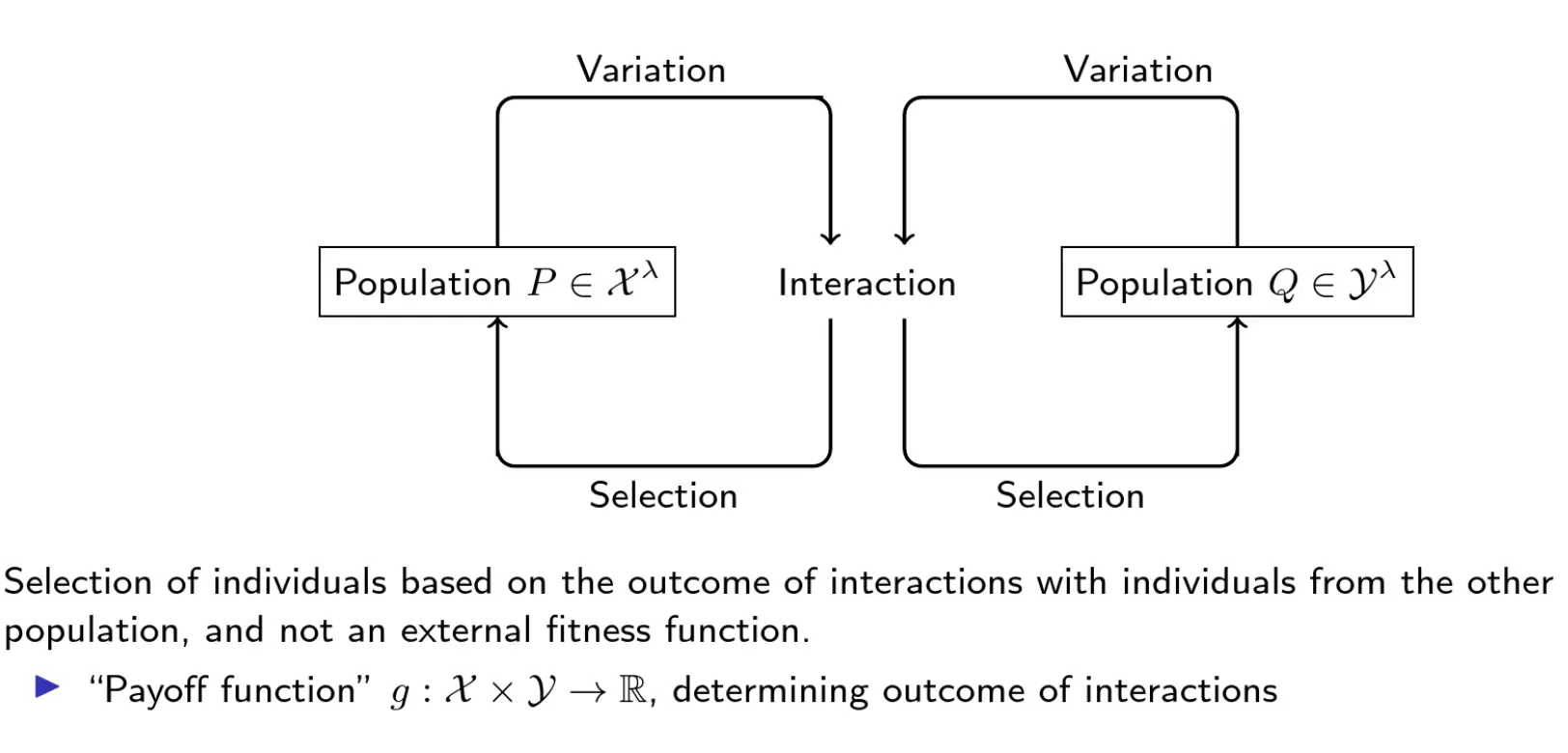这是两个相互进化的种群，其中左边可能是猎食者，右边可能是猎物。共进化的流程是这样的：

1. 变异，没什么好说的
2. Interaction：两个种群两两交互，产生对抗结果，每对个体(x,y)的交互由payoff function也就是g(x,y)决定（例如胜负得分）
3. Selection：选择，个体的好坏由他与对方的交互中体现，没有单独的fitness function，而是基于互动结果选择保留谁。

Sorting Networks的共进化

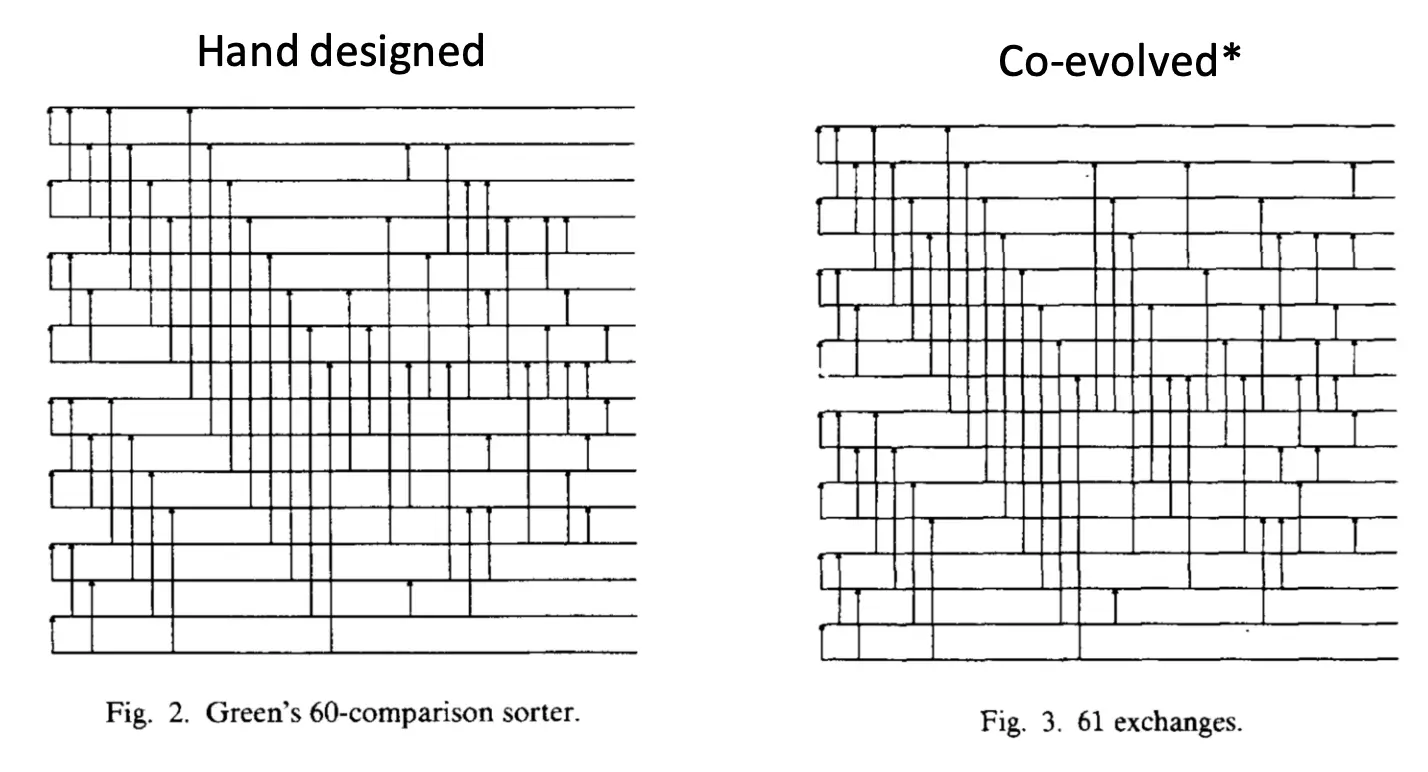
什么是Sorting Network？其实就是在元素数量一定时的一套固定比较规则，按这个规则比完肯定能sort成功，如图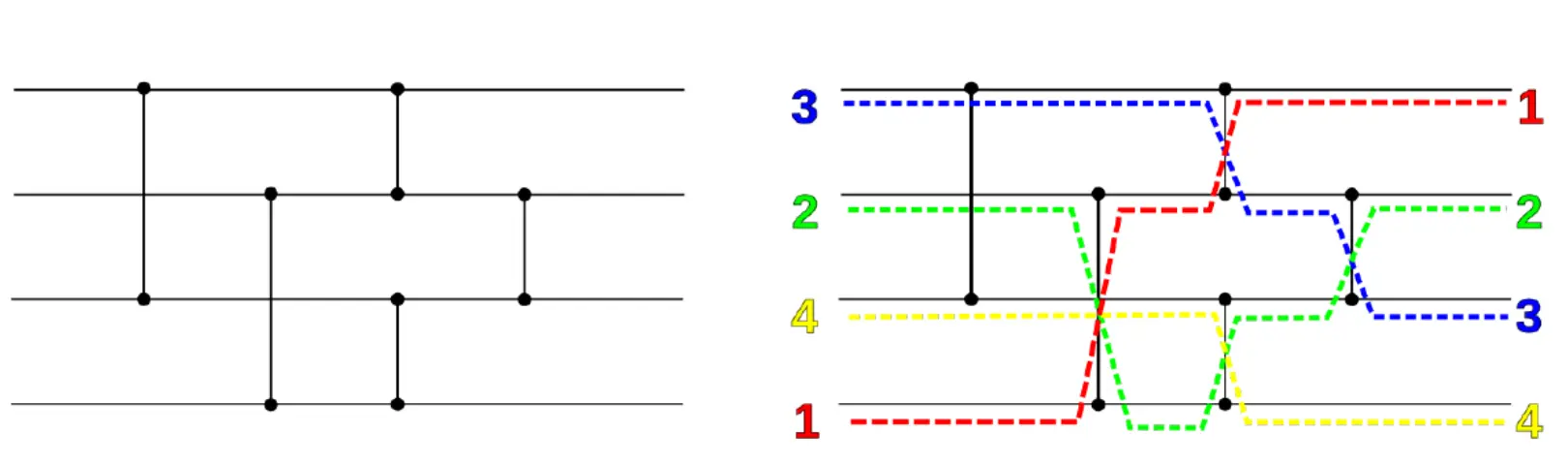： 横轴是时间，竖着连就是比较，如果下面的小于上面的，那么就swap。网络是否好就是看给定元素的情况下比较次数越少越好。 人为设计的sorting network，在元素n=16的情况下，1962年的最佳是65，一直到1969年不断优化有了60比较的网络设计。

那么如何用传统EA来表示这个问题并解决呢？

传统EA解决n = 16 Sorting Networks

个体：一个sorting network 基因型：一串有序的比较方法。比如(1,4) (3,2) 表示先1和4比，如果1比4小，那么交换，然后是3和2比。一共有15对染色体，每个染色体表示四个比较。16个元素，那么4位就能代表一个数，8位代表一个比较，32位就是4个比较，15对32位的染色体就是120个。 fitness function：给n个测试样例，看看百分之多少可以被正确排序

• 问题：全部测试太慢，但只测试一小部分可能会错过bug。 首次试验：
• 所有个体不是随机混合，而是分布在一个二维网格上（像棋盘一样），相邻个体交配，远处的不能直接影响彼此 → 保留多样性。
• 适应度由随机子样本计算，没有用全部测试输入来算 fitness，而是从所有输入中随机选一部分样本，加快评估速度
• 适者生存 + 替换策略，每一代把适应度低的一半个体“淘汰”，用邻居中适应度高的个体的拷贝来替换（不是随机重生）
• 局部配对繁殖，个体只和自己附近的个体进行配对、交叉，避免全局交配导致“基因污染”，进一步增强多样性。
• 特殊的交叉方式 + 微小变异，使用专门为“双倍体染色体”设计的交叉操作；然后用很小概率（$p_m=0.001$）进行变异，增加新的基因组合；
• 超大规模种群，种群大小在 512 到 100 万之间尝试；
• 最终结果，发现了一个只用 65 个比较器 的排序网络，这是个很棒的结果，说明方法确实能优化出高效网络。

什么是二维网格？什么是局部配对繁殖替换？
如果有9个个体（9个网络），那么就这样安排：
A B C  
D E F  
G H I
每个字母是一个个体，这样，A就只能和B，B繁殖，而不是随便找全局最优，鼓励了多样性。

什么是局部配对繁殖替换？如果E很拉死掉了，那么就从(B, D, H, F)中挑一个强的复制一份替代E的位置。

为什么传统EA没有表现的更好？

• test cases可能会过拟合，因为一直不变，难度也不变。 那么co-ea怎么解决问题？

Co-EA解决n = 16 Sorting Networks

双边共进化:

• 一边进化 排序网络（Predator）→ 想办法把输入排对；
• 一边进化 测试用例（Prey）→ 想办法“绊倒”排序网络（给它出难题）； Result: 61 Comparisons, 比65要好。这很像GAN。

Patching Buggy Software的共进化

问题描述： 给你一个输入，为有bug的程序。 另一个输入，为形式化的规格说明（Formal Specification），用逻辑或语言明确地写出程序的“应有行为”。它包括两部分，

• Pre-condition（前置条件）：程序开始前应该满足的条件；
• Post-condition（后置条件）：程序运行后应该满足的结果条件。 我们能不能只看“规格说明”就自动找出程序里的 bug，并修好它？

那么程序bug自动修复的过程就是这样的coea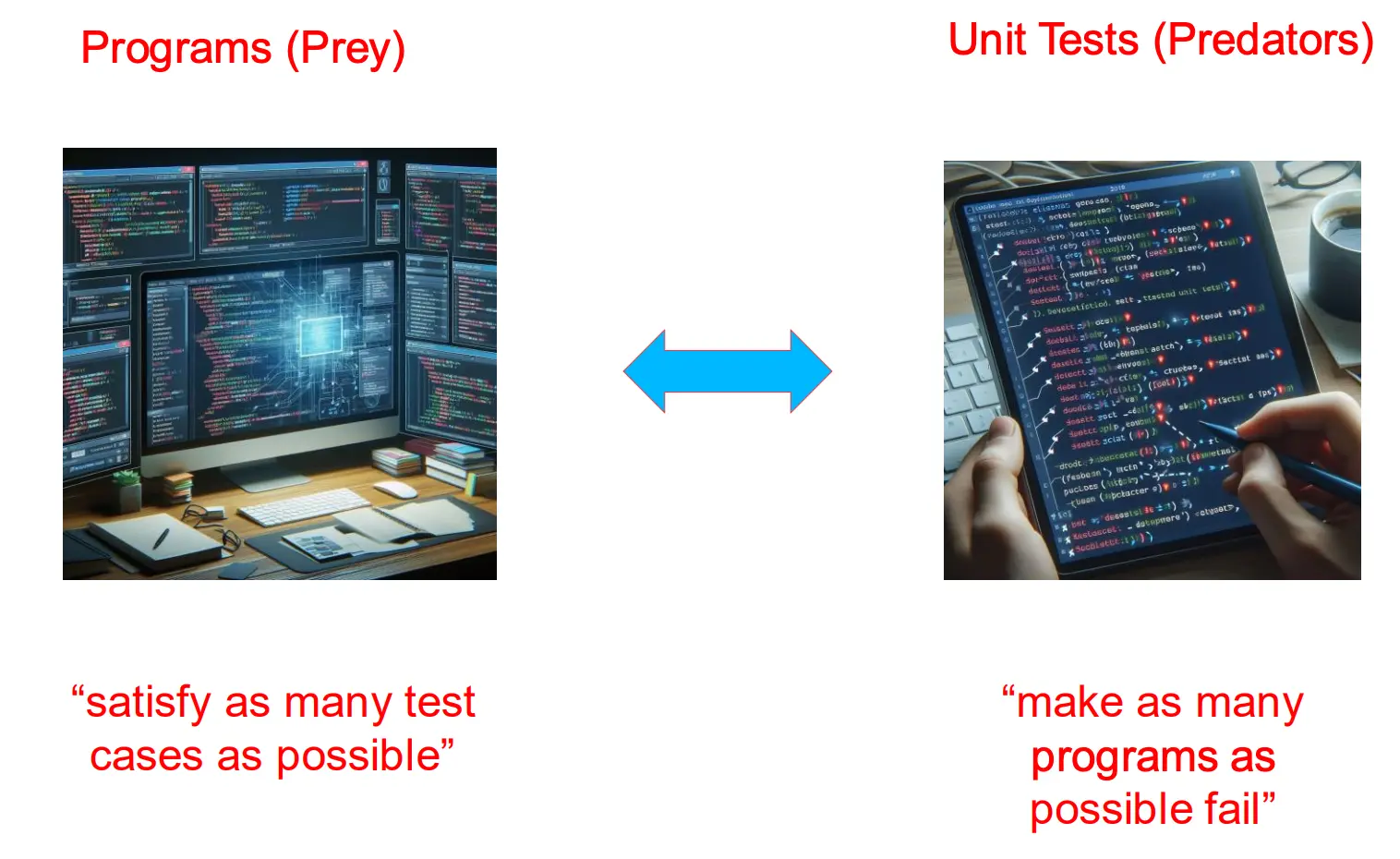： 过程就是，创建一组程序个体（种群 $Q_0$）；初始个体来自那个有 bug 的程序；后面这些程序会逐渐变异、进化，尝试变“对”。 然后随机生成一批单元测试（种群 $P_0$）；用这些测试来检验程序对不对。

当前的程序个体会被用来执行“Hall of Fame”（一个测试用例集合）里的测试； 表现越好的程序（通过越多测试）适应度越高； 然后遗传选择、变异、交叉来进化出新一代程序。

同样地，测试用例也进化，目标是生成更“刁钻”的输入，能挑出程序的 bug。

从这一代的测试种群中选出最能发现程序错误的测试； 加入“Hall of Fame”永久保存，供后续评估用。

在某些阶段，可能会专门让测试用例进化很久（比如 1024 代）； 这时用当前最好的程序作为目标，进化出能打败它的测试用例，逼它变得更鲁棒。

COEA自动修复bug挑战

1. 原始程序虽然不完美，但它可能只是错了一点点；它结构上很可能接近正确版本；所以它的“fitness”分数虽然低，却不能直接被淘汰。
2. Buggy 程序容易被“迷惑性的高分短程序”淘汰。进化过程中，有些程序可能因为写得更短、更简单，对现有测试过拟合；fitness 看起来高，但本质上没解决核心问题；导致原始 buggy 程序被遗传算法“忘掉”。 那么应对策略就是：

• 定期重新引入原始 buggy 程序，为了防止遗忘，把原始程序定期加回种群中，保持其基因存在。
• 惩罚明显太短的程序， 作者认为，在这个任务中，突变比交叉互换更有用。 另一个就是distance function的引入。试想，如果只用对了或者错了来评判一个程序对测试集的适应程度，那么粒度有点大了。所以引入distance function来减小粒度。 拿A=B为例，其实就是一个设计标准。如果A=B满足的话，那么distance function应该为0，不然的话，应该就是abs(a-b) + K。这些就是一个规范，告诉你应该怎么设计。

那么有了这个distance function（基于x和y的），那么就可以推导出两个fitness function：

总结

共进化（Co-evolution） 和 遗传编程（Genetic Programming） 结合起来，来自动修复带 bug 的程序。

• 程序种群不断演化尝试修复自身；
• 测试种群同时演化以发现更多 bug；
• 使用形式化规格来定义适应度（fitness）；
• 使得评估更精确、可区分、可推进。

和传统机器学习的区别 ML可以容忍误差、噪声，COEA Debugging必须完全满足每个测试 ML过拟合不好，COEA “过拟合每个测试”是目标

自动修复不是万能的 并不是所有 bug 都能被自动修复，尤其是像停机问题，判断一个程序是否会停机，本身在理论上是不可判定的（图灵不可判定性）。

Incremental Predator-Prey Co-Evolutionary Algorithm (IPCA)

首先复习帕累托支配。 两个猎食者x1，x2，如果在猎物集合Q上，x1在每个猎物上都不差于x2，也就是说

$$\mathrm{\forall }y\in Q,g(x_1,y)\ge g(x_2,y)$$

那么我们说，在Q上x1支配x2

一组捕食者P，面对猎物集合Q，如果存在x' <- P, x'支配x，那么称P支配x

那么IPCA的伪代码如下： 流程：首先有P和Q两个种群，P是猎食者，Q是Prey。Q如果牛逼可以支配P中的。 所以首先保留P中不被Q支配的个体x，然后生成新的predators和preys， 之后，先从新的preys中增加可以使Q不被P支配的个体（新猎物 $y$ 可以揭露新捕食者 $x$ 的弱点（即加入 $y$ 之后，$x$ 被支配了）），然后对于每个新产生的predators，增加可以支配Q的个体。

IPCA总结

IPCA是单调的，因为Prey不会被删除，捕食者只在被支配时才被移除，所以不会误删有价值的捕食者。整个系统的性能是“单调变好”的。 然而，保证单调变好也不一定能在合理的时间内找到解，因为Q可能变得巨大。

Pairwise Dominance Co-Evolutionary Algorithm (PDCoEA)

帕累托支配有个问题，就是判断帕累托支配的代价有点高，要考虑全局。 首先忘掉帕累托支配，我们现在定义一种新的支配，Pairwise Dominance 成对支配

成对支配的定义：考虑一个对抗系统x1, x2, y1, y2, g(x,y) 表示狼在兔子上的表现（越高越好），我们希望比较两个对抗组合哪个更强。 (x1,y1)支配(x2, y2)的意思是，x1和x2交换猎物，x1打y2能更牛逼，而x2打y1不如x1打y1，也就是说，x1，x2在面对y1, y2的时候，x1更厉害一点，y1, y2里面y1厉害一点，所以用x1打y1.

那么PDCoEA的伪代码如下：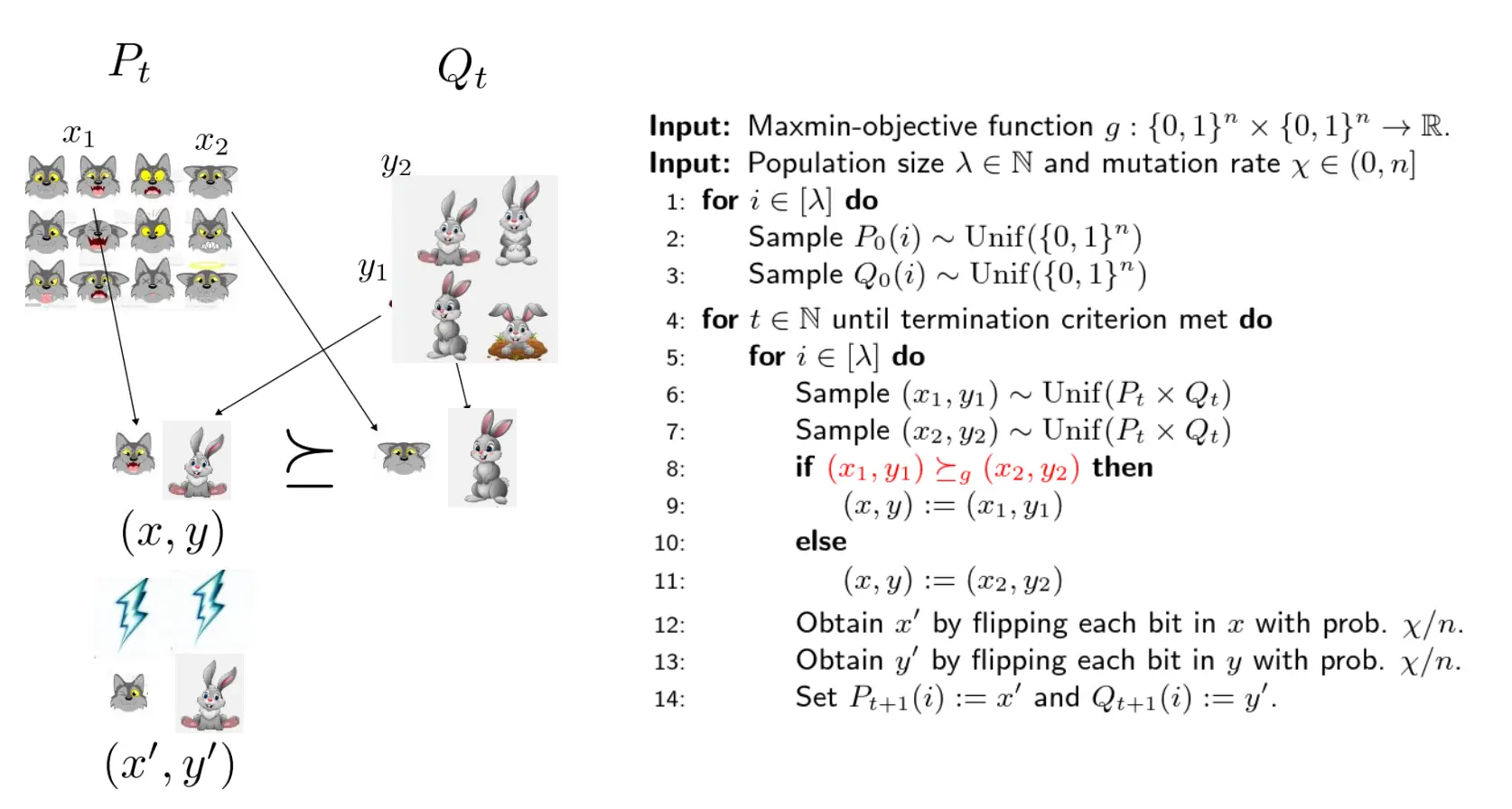

这个框架下，选取能能pairwise支配的x, y作为下一代的基础，然后突变放入下一代种群。 PDCoEA 是首个具备运行时理论分析的共进化算法。
在合理突变率下它能高概率多项式时间找到最优解，
虽然不保证每一代都改进，但整体上收敛快、表现稳定。

总结

共进化适用于这种对抗性问题（minmax） CoEA = 模仿自然共进化的算法，用于对抗优化 IPCA具有“单调进展性”，每一代都保存最强个体（不能退步），但可能效率较低，不够激进，容易停滞。 PDCoEA没有强制单调性（有可能临时退步）；但平均而言是正漂移（positive drift）；在 bilinear 问题上，有期望多项式时间收敛（expected polynomial runtime）；更轻量、简单、适合大规模共进化。

共进化是一种模拟自然对抗演化机制的优化策略，
被成功应用于排序网络设计、程序修补等领域，
IPCA 和 PDCoEA 是其中两种代表性算法，各有取舍：

• IPCA 保守但稳定；
• PDCoEA 激进但高效。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update