Bias and Variance

字数

2261 字

阅读时间

10 分钟

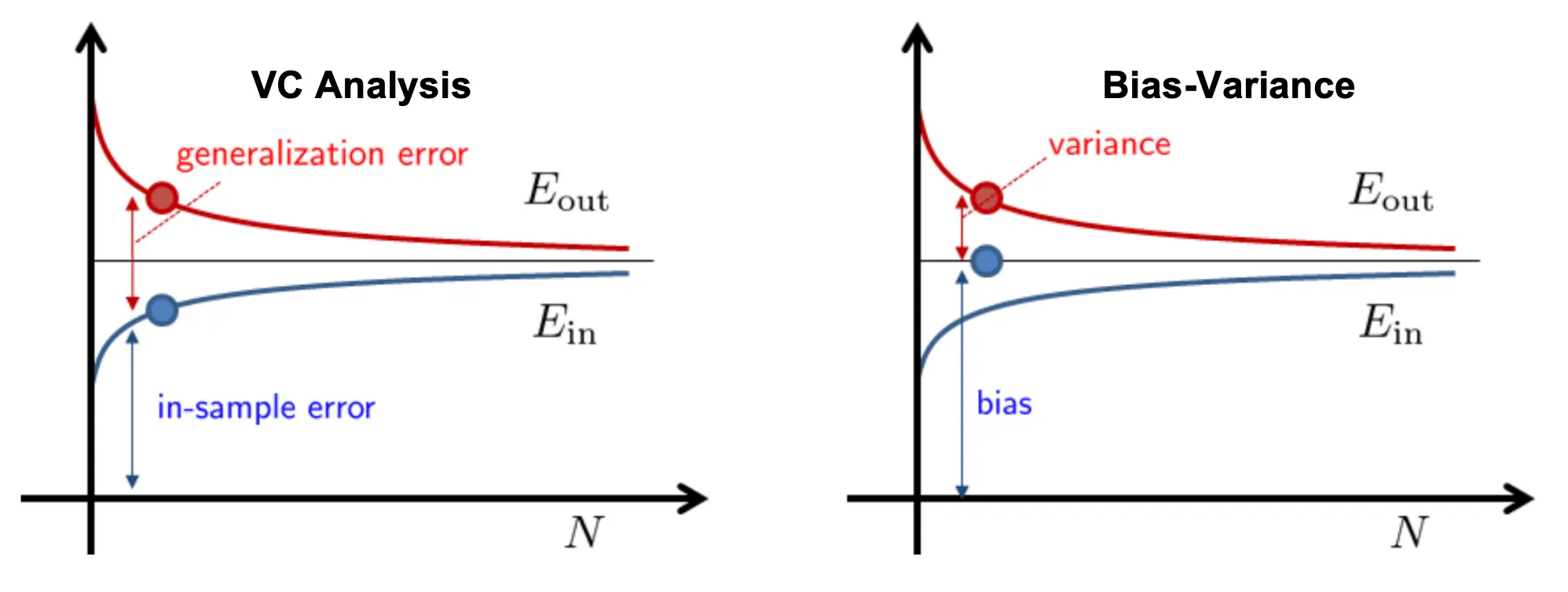
上一节的VC Bound分析我们主要关注二分类问题，来分析泛化误差。这一节我们来分析Bias-Variance，主要来分析回归的平方误差。

$$\underset{\text{欠拟合}}{\underbrace{{\mathrm{Bias}}^2}}+\underset{\text{过拟合}}{\underbrace{\mathrm{Variance}}}+\underset{\text{数据本身不可学}}{\underbrace{\mathrm{Noise}}}.$$

VC分析回顾

如果学习是feasible的，那么

$$E_{\mathrm{out}}(g)\approx E_{\mathrm{in}}(g)$$

第二步，我们需要保证

$$E_{\mathrm{in}}(g)\approx 0$$

所以Learning被拆成了两个部分

1. 让Eout和Ein足够近
2. 让Ein离0足够近

而模型复杂度的上升（d的上升）会导致Ein减少，而Eout和Ein的差距会变大。

我们学到了这些东西：

• VC dimension就是 $d_{\mathrm{VC}}(\mathcal{H})$ 表示H能shatter的最多点数
• 泛化被表示分析成了一定置信度下， $E_{\mathrm{out}}\le E_{\mathrm{in}}+\mathrm{\Omega }$
• VC分析的scope
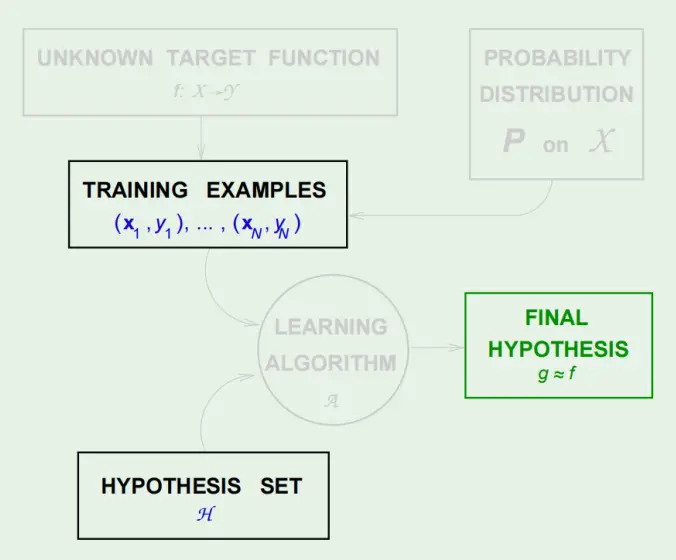
• VC分析的效用曲线

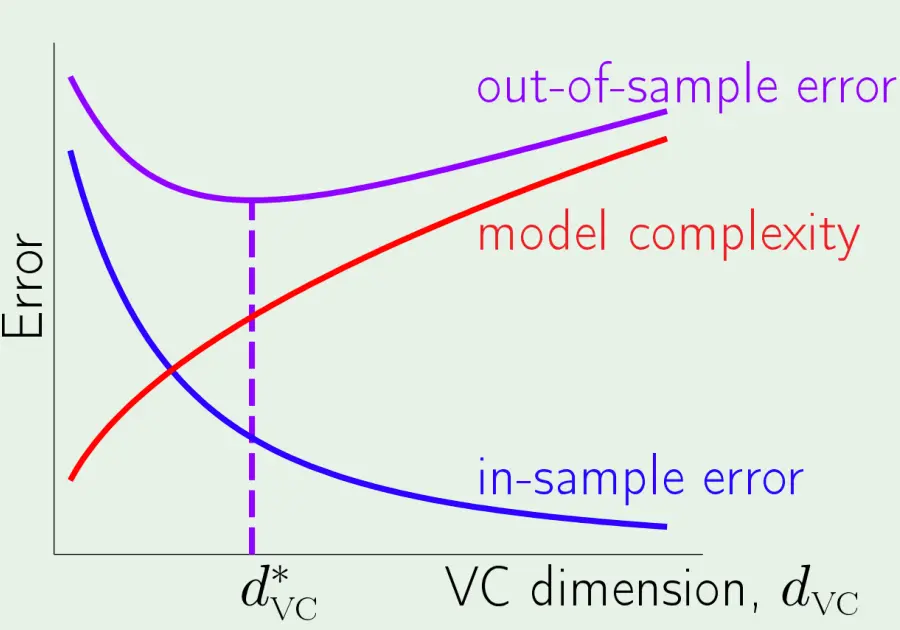
VC分析的分析对象是一个二分类问题。如果我们把二分类问题的泛化误差写成期望形式：

$$\begin{array}{r}{E}_{\mathrm{out}}(g)=\mathbb{P}[g(\mathbf{x})\ne f(\mathbf{x})]\end{array}$$

就有

$$\begin{array}{rl}{E}_{\mathrm{out}}(g)& \begin{array}{r}=\mathbb{P}[g(\mathbf{x})\ne f(\mathbf{x})]\end{array}\\ & =\mathbb{P}[B=1]\\ & \begin{array}{r}=1\cdot \mathbb{P}[B=1]+0\cdot \mathbb{P}[B=0]\end{array}\\ & =\mathbb{E}[B].\end{array}$$

那么就说明了泛化误差就是出现坏事件的期望

$$\begin{array}{r}{E}_{\mathrm{out}}(g)={\mathbb{E}}_{\mathbf{x}}[\mathbf{1}\{g(\mathbf{x})\ne f(\mathbf{x})\}],\end{array}$$

Intro of Bias and Variance分析

两者都是理解“为什么训练误差小不一定意味着测试误差小”的工具。 我们VC分析把泛化误差拆成了高概率的误差上界：

$$E_{\mathrm{out}}\le E_{\mathrm{in}}+\mathrm{\Omega }$$

而BV分析是另一种拆法，拆成了：

1. H有多逼近f
2. H有多聚焦于好的h, 其中h <- H 这样的分析，我们就用到real-valued targets以及squared error

VC

对于VC Analysis，我们用的例子是分类任务。分类任务我们采用的Eout衡量方法是0-1 Loss

$$E_{\mathrm{out}}(g)={\mathbb{E}}_{\mathbf{x}}[\mathbf{1}\{g(\mathbf{x})\ne f(\mathbf{x})\}]$$

而通过Hoeffding，我们能以高概率保证

$$E_{\mathrm{out}}(g)\le E_{\mathrm{in}}(g)+\mathrm{\Omega },$$

这是一种“最坏情形”分析，不论你用什么训练集D，也不管选出的g是哪一个，只要H的VC bound有限，上界就成立。

BV

对于BV，我们用的例子是回归任务，Eout我们用平方损失衡量

$$\begin{array}{r}{E}_{\mathrm{out}}(g)={\mathbb{E}}_{\mathbf{x}}[(g(\mathbf{x})-f(\mathbf{x}){)}^2]\end{array}$$

对于一个从整体数据中采样出的训练集D，Eout为：

$$E_{\mathrm{out}}(g^{(D)})={\mathbb{E}}_x[(g^{(D)}(x)-f(x){)}^2]$$

而我们要在整个数据中进行多次采样训练集，所以要对整个过程求一个E。

$${\mathbb{E}}_{\mathcal{D}}[E_{\mathrm{out}}(g^{(\mathcal{D})})]={\mathbb{E}}_{\mathcal{D}}\left[{\mathbb{E}}_{\mathit{x}}[(g^{(\mathcal{D})}(\mathit{x})-f(\mathit{x}){)}^2]\right]$$

这是一种“平均情形”分析，与你采样D的过程是有关的。

BV分析推导

接下来，我们尝试推导一下BV分析。x为test sample。 首先我们有：

$$E_{\mathrm{out}}(g^{(\mathcal{D})})={\mathbb{E}}_{\mathbf{x}}\left[{(g^{(\mathcal{D})}(\mathbf{x})-f(\mathbf{x}))}^2\right]$$

而由于这个过程和D的采样有关，所以我们对D求一个期望：

$${\mathbb{E}}_{\mathcal{D}}[E_{\mathrm{out}}(g^{(\mathcal{D})})]={\mathbb{E}}_{\mathcal{D}}\left[{\mathbb{E}}_{\mathbf{x}}\left[{(g^{(\mathcal{D})}(\mathbf{x})-f(\mathbf{x}))}^2\right]\right]$$

然后，由于ED和EX都可积，所以可以交换顺序：

$$={\mathbb{E}}_{\mathbf{x}}\left[{\mathbb{E}}_{\mathcal{D}}\left[{(g^{(\mathcal{D})}(\mathbf{x})-f(\mathbf{x}))}^2\right]\right]$$

外层的Ex处理“我随机抽一个x到总体上去测试，内层的ED处理“在这个固定的x下，因为训练集不同模型输出会有波动。我们先“冻住”一个x，专注于内部的这一部分：

$${\mathbb{E}}_D\left[{(g^{(\mathcal{D})}(\mathbf{x})-f(\mathbf{x}))}^2\right]$$

我们首先定义一个辅助对象 $\overline{g}(x)$ 。它是所有可能训练集D下到的模型输出在点x上的平均值：

$$\overline{g}(\mathbf{x})={\mathbb{E}}_D[g^{(\mathcal{D})}(\mathbf{x})]$$

有了这个辅助对象后，原先的那个就可以变成：

$${\mathbb{E}}_D\left[{(g^{(\mathcal{D})}(\mathbf{x})-f(\mathbf{x}))}^2\right]={\mathbb{E}}_D\left[{(g^{(\mathcal{D})}(\mathbf{x})-\overline{g}(\mathbf{x})+\overline{g}(\mathbf{x})-f(\mathbf{x}))}^2\right]$$

配方就可以写成：

$$={\mathbb{E}}_{\mathcal{D}}[{(g^{(\mathcal{D})}(\mathbf{x})-\overline{g}(\mathbf{x}))}^2+{(\overline{g}(\mathbf{x})-f(\mathbf{x}))}^2+2(g^{(\mathcal{D})}(\mathbf{x})-\overline{g}(\mathbf{x}))(\overline{g}(\mathbf{x})-f(\mathbf{x}))]$$

而由于前面有ED，最后的交叉项的乘积最后为0，所以可以化简为：

$$=\underset{\mathrm{var}(\mathrm{x})}{\underbrace{{\mathbb{E}}_{\mathcal{D}}\left[{(g^{(\mathcal{D})}(\mathbf{x})-\overline{g}(\mathbf{x}))}^2\right]}}+\underset{\mathrm{bias}(\mathrm{x})}{\underbrace{{(\overline{g}(\mathbf{x})-f(\mathbf{x}))}^2}}$$

所以最一开始的原式可以化简为：

$${\mathbb{E}}_D[E_{\mathrm{out}}(g^{(\mathcal{D})})]={\mathbb{E}}_{\mathbf{x}}\left[{\mathbb{E}}_D\left[{(g^{(\mathcal{D})}(\mathbf{x})-f(\mathbf{x}))}^2\right]\right]$$$$={\mathbb{E}}_{\mathrm{x}}[\mathrm{bias}(\mathrm{x})+\mathrm{var}(\mathrm{x})]$$$$=\mathrm{bias}+\mathrm{var}$$

偏差 = 平均预测与真实目标的误差，反映“欠拟合”程度； 偏差大说明假设空间或学习过程本身“欠拟合”了真实函数。适当的偏差并非坏事：有时候引入一点偏差可以显著降低方差，从而提高整体泛化性能。

方差 = 预测值在不同训练集下的波动，反映“过拟合”趋势； 方差高说明模型对训练数据的微小变化非常敏感，容易过拟合。增加训练样本数使用正则化或集成方法（bagging、dropout 等）都能有效减少方差。

泛化误差 ≈ Bias² + Variance + Noise（二者之和，再加上数据本身的不可约噪声）。

BV分析例子

sin函数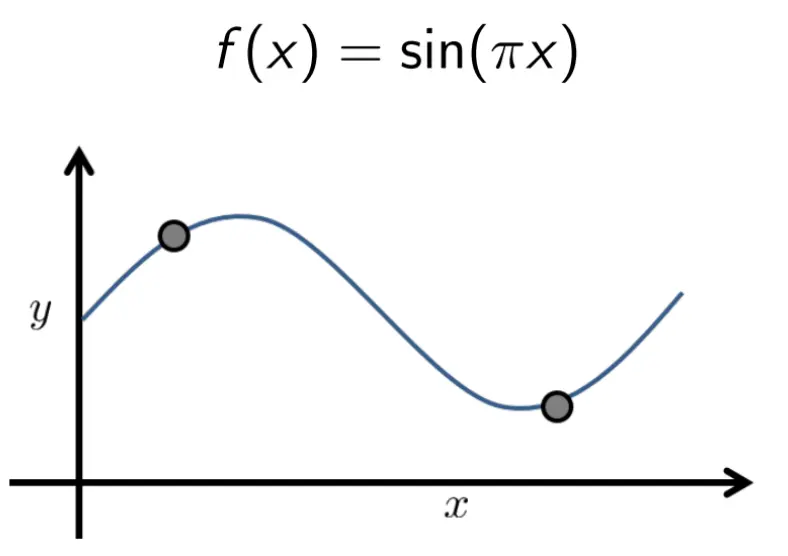 假设集1: h(x) = b 假设集2: h(x) = ax + b

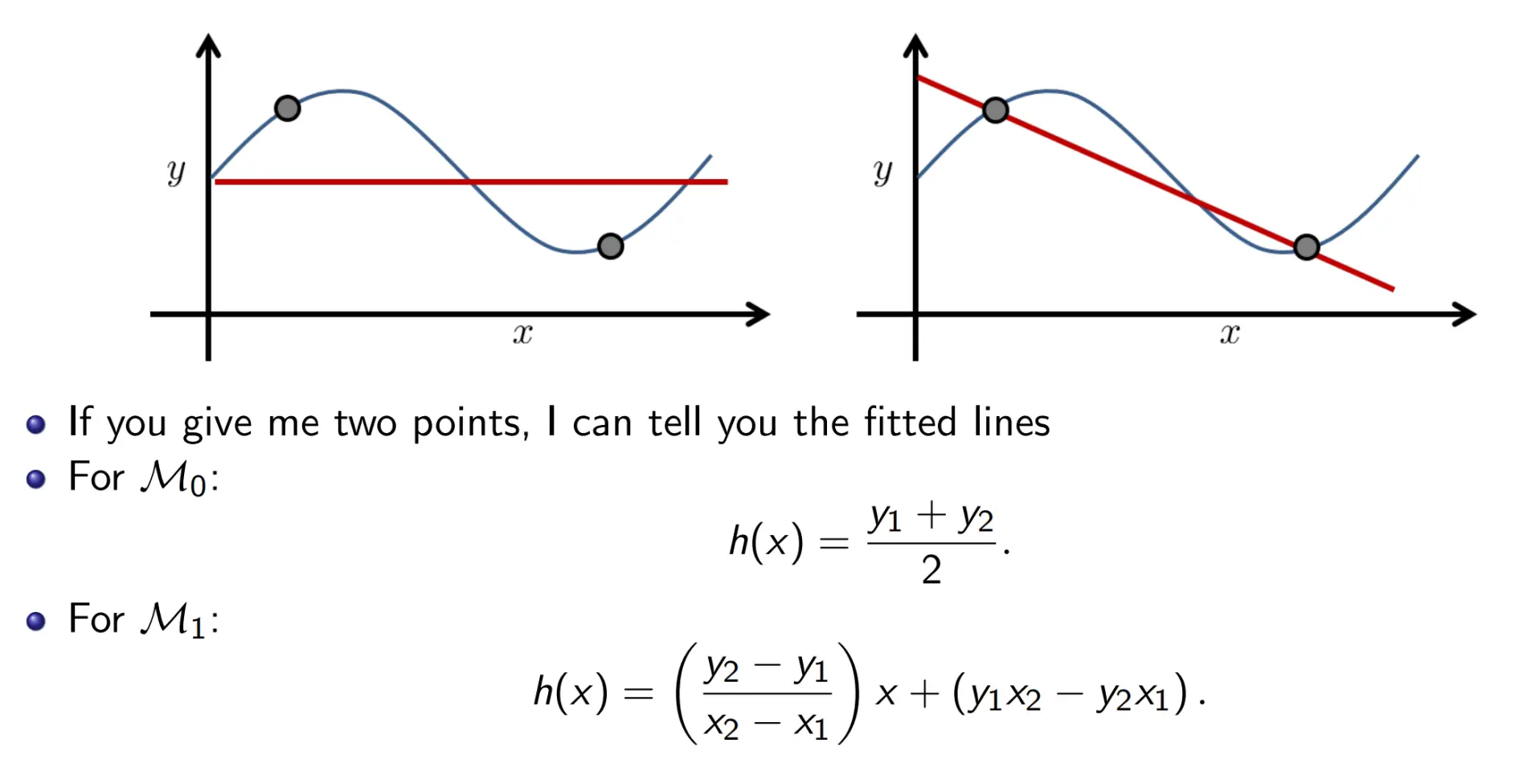那两个点就相当于是训练集D。现在，我们对两点多次采样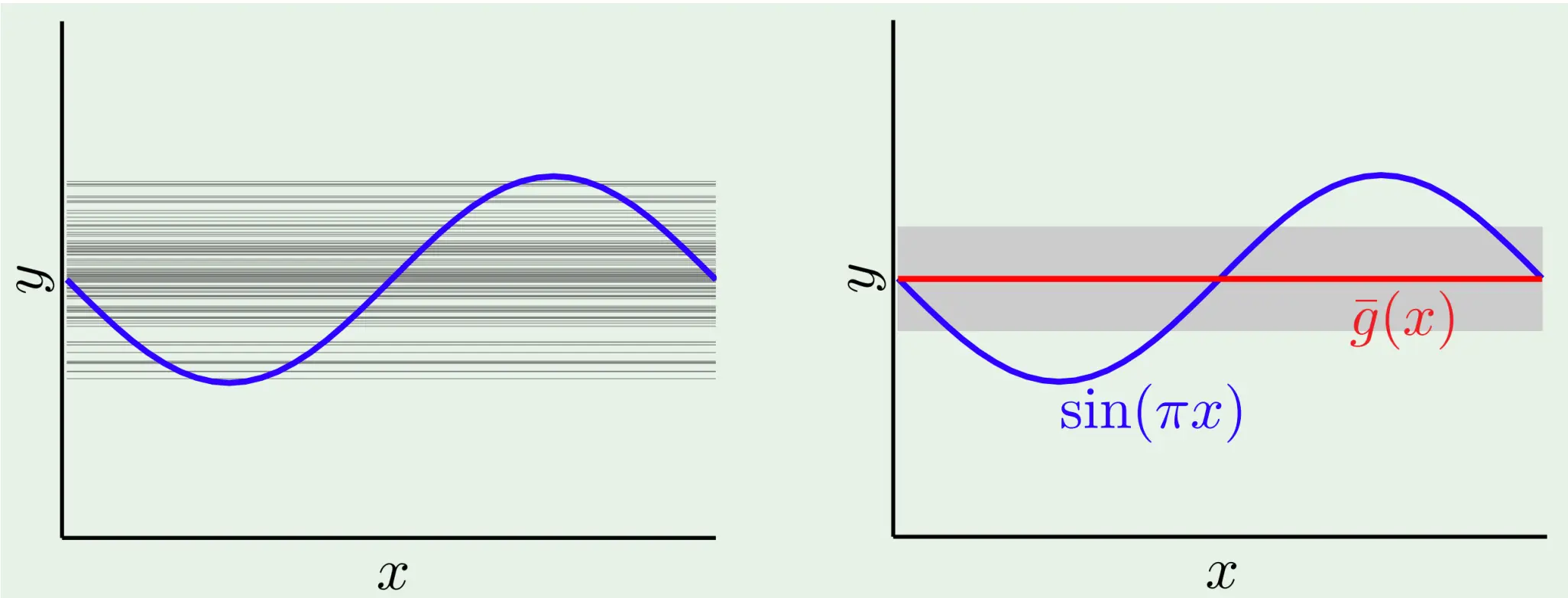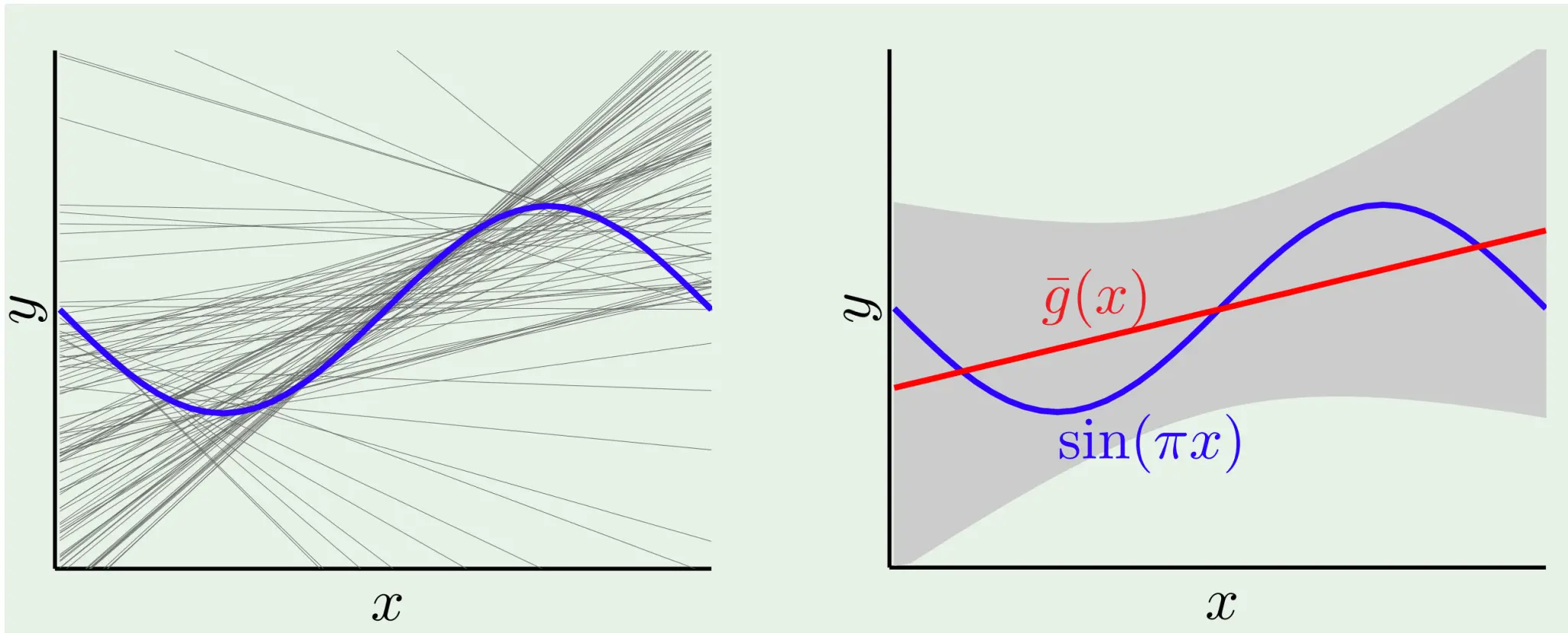： 那么我们有结果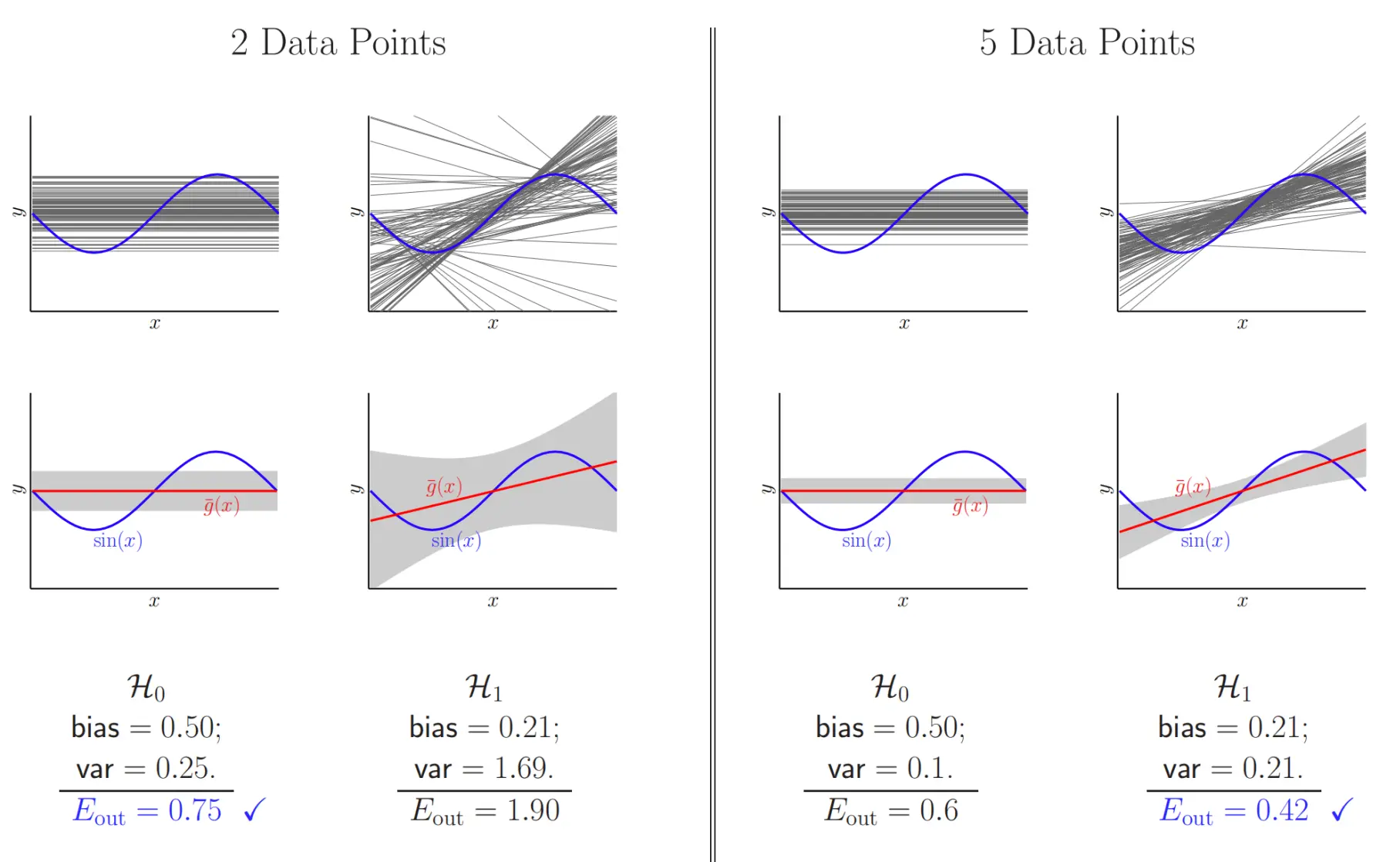： 我们可以给出简单模型和复杂模型的学习曲线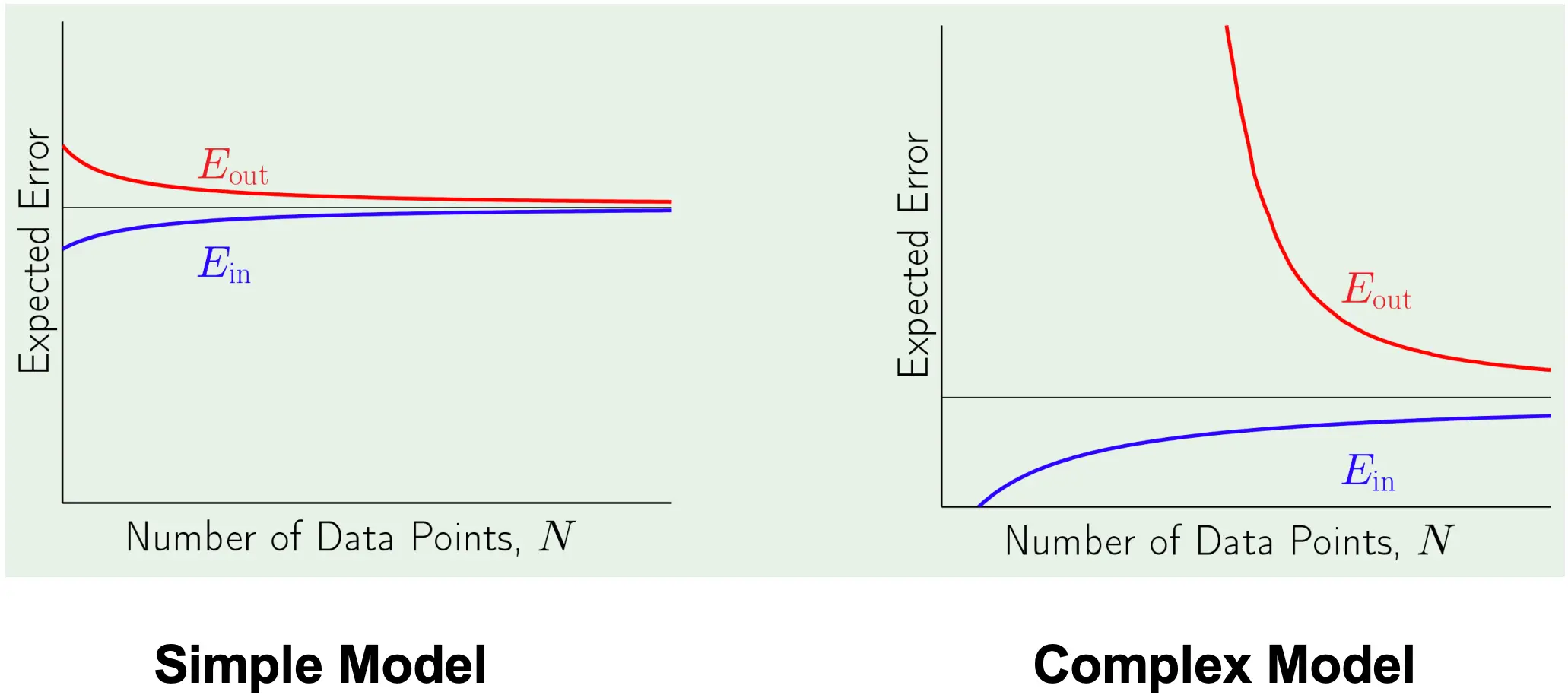： 我们定义训练集D的大小为N，对于每个D，我们训练出模型g(D)。sigma方表示数据本身的噪声方差，是任何模型在x上都不可约的误差。 如果模型容量（例如特征维度）是d，当样本数刚好N = d+1 时，线性模型通常可以把训练误差拟合到接近零，但较小的数据会导致模型对噪声过度拟合，方差大。而随着N不断增长后，Ein会上升，因为可过拟合的自由度减少，模型越来越难把训练集误差压到 0，Eout会下降，因为更多数据能更好地估计真实函数，模型方差（对训练集的敏感度）降低。如果把N推导极限，都会收敛到同一个水平，也就是数据本身的噪声方差sigma方。 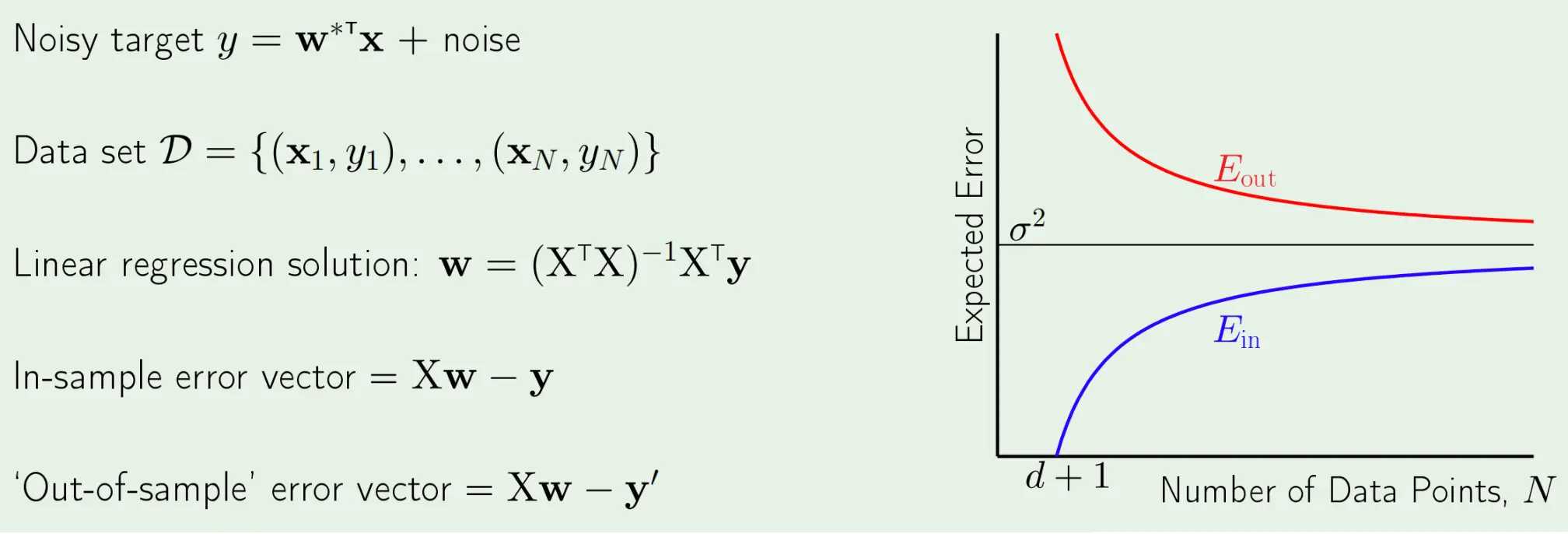经过数学推导可以得到： 可以可视化为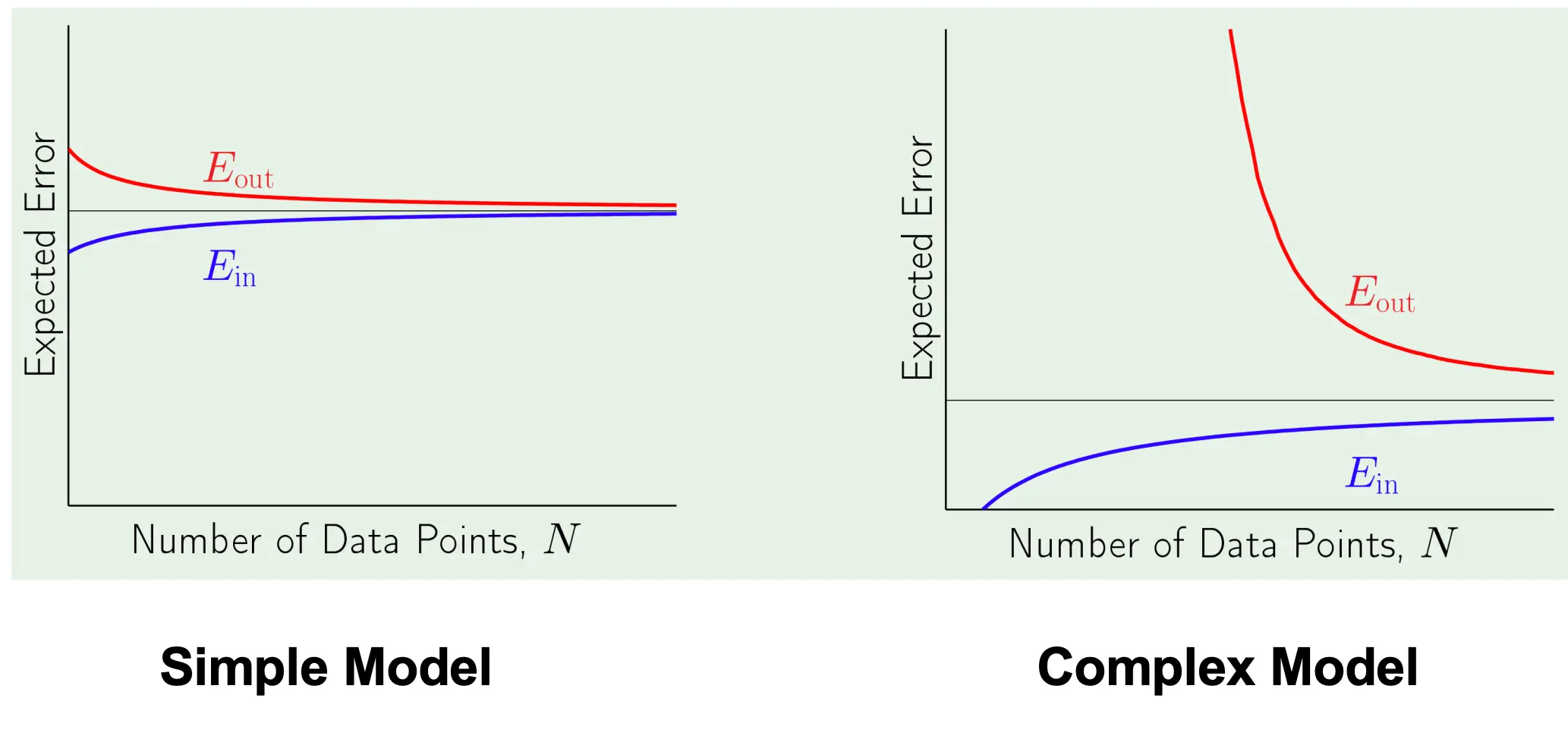： 我们再来看这张图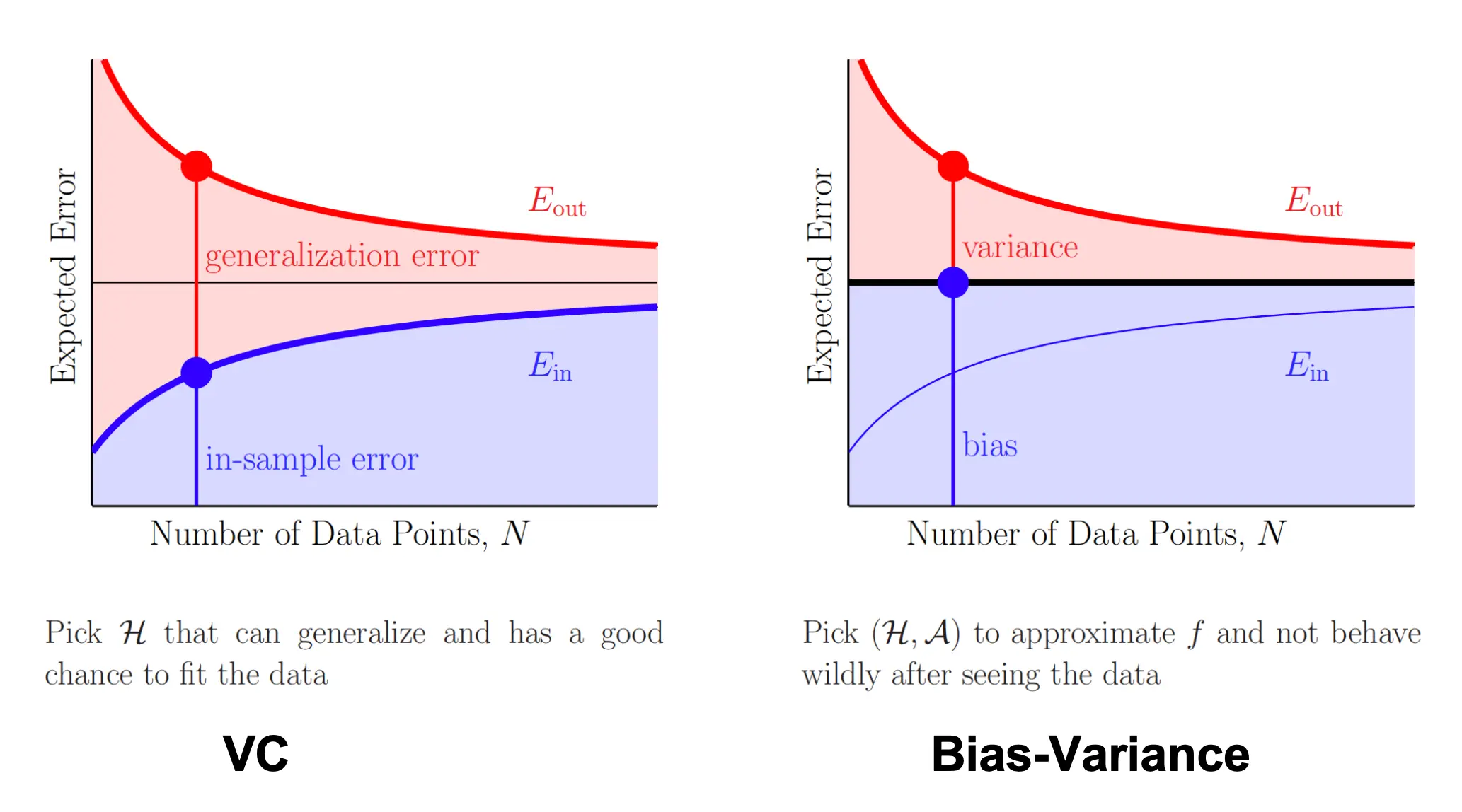： 由于VC分析 $E_{\mathrm{out}}\le E_{\mathrm{in}}+\mathrm{\Omega }$ ，所以泛化误差Eout - Ein就是红色部分。 由于BV分析 $E_{\mathrm{out}}={\mathrm{Bias}}^2+\mathrm{Var}+\mathrm{Noise}$ 。

对于VC分析，他关心：

• 你有没有把训练数据拟合得足够好？（Ein​）
• 你的 Ein​ 能否高概率地推广到 Eout​？（Ω） 条件：不能在选定H前偷看数据。

对于BV分析，他关心：

• 你的假设集 H最好能拟合真实目标 f 多少？（Bias）
• 在有限数据下，你能多稳定地逼近那个最佳拟合？（Variance） 条件：需要对所有可能训练集 D 做期望

Noise

有哪些噪音呢？ y的噪音：

• 误标记：本来是个好客户，却被标成“坏”
• 标签不一致：同一客户在不同时间、不同评审员那里被标了不一样的结果 x的噪音：
• 重要变量缺失：比如家庭背景、还款意愿等关键因素没收集到

如果我们用弹珠来举例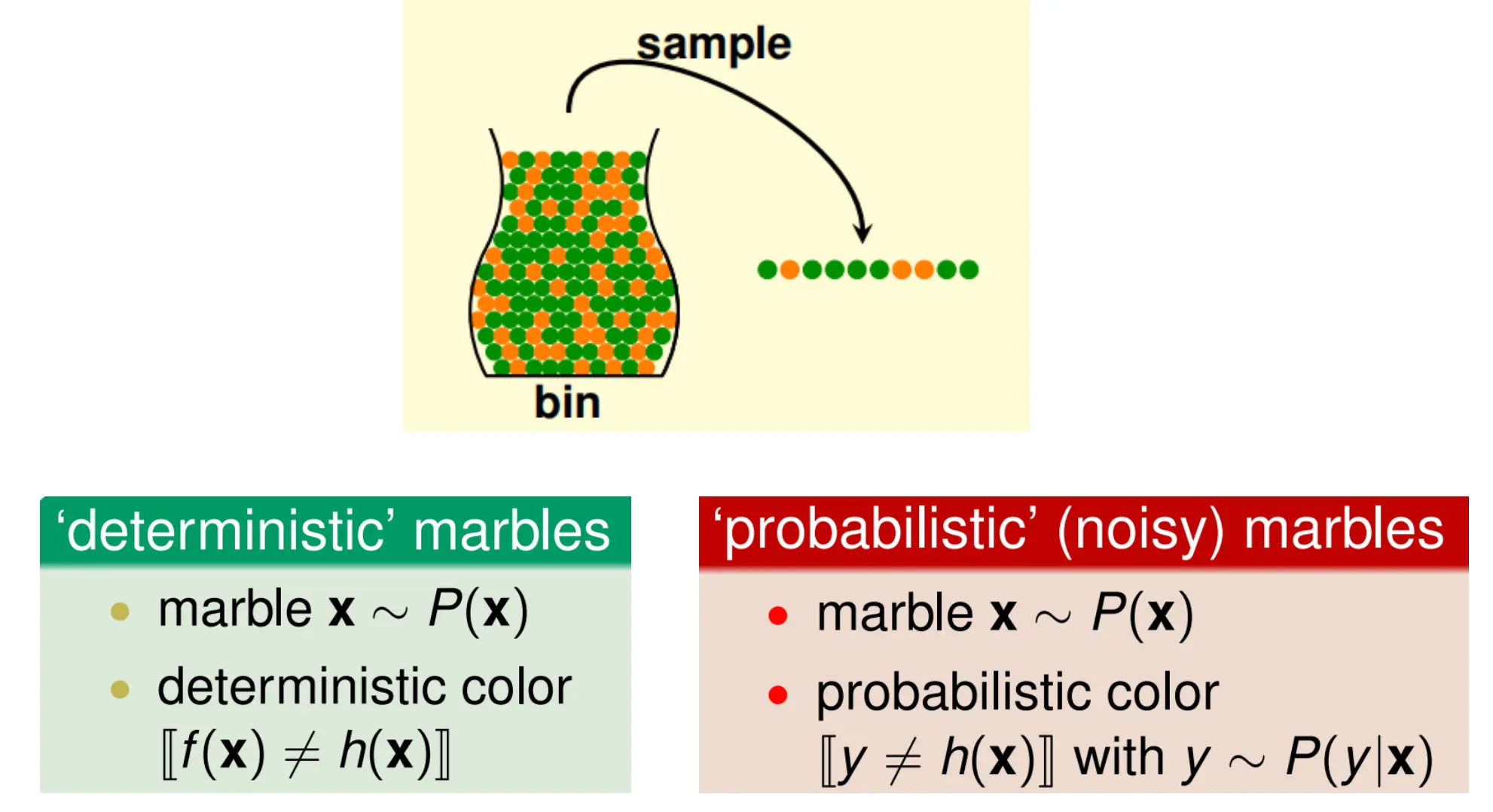： 那么分为确定性弹珠以及噪音弹珠 对于确定性弹珠，每个特征点x都有一个固定的真标签f(x), 无论你对同一个x抽多少次，颜色永远相同。 对于噪音弹珠，同一个 x 每次抽出时都会随机“变色”，他的标签y是按条件分布P(y|x)抽的。所以即便特征完全一样，也会因为标签噪声而出现不同的颜色。这玩意其实就是不可约噪音。

那么我们尝试把这个噪音融入到我们的框架中。

对于确定性的marbles，每输入一个x对应一个固定的真标签y=f(x) 对于不确定性的噪音marbles，其标签y服从一个概率：

$$P(y\mid x).$$

所以训练样本(x,y)不再是(x, f(x))，而是一个联合分布：

$$P(x)P(y\mid x)$$

其实确定性的f(x)也可以当做是一个特殊的噪声分布，比如：

$$P(y\mid x)=\{\begin{array}{ll}1,& y=f(x),\\ 0,& \text{否则,}& & \end{array}$$

至此，我们的目标就是学习这个P(y|x), 它包含了x对标签的平均影响f(x)，以及噪声的随机性。输入分布为P(x)。 于是带噪音的框架就是这样的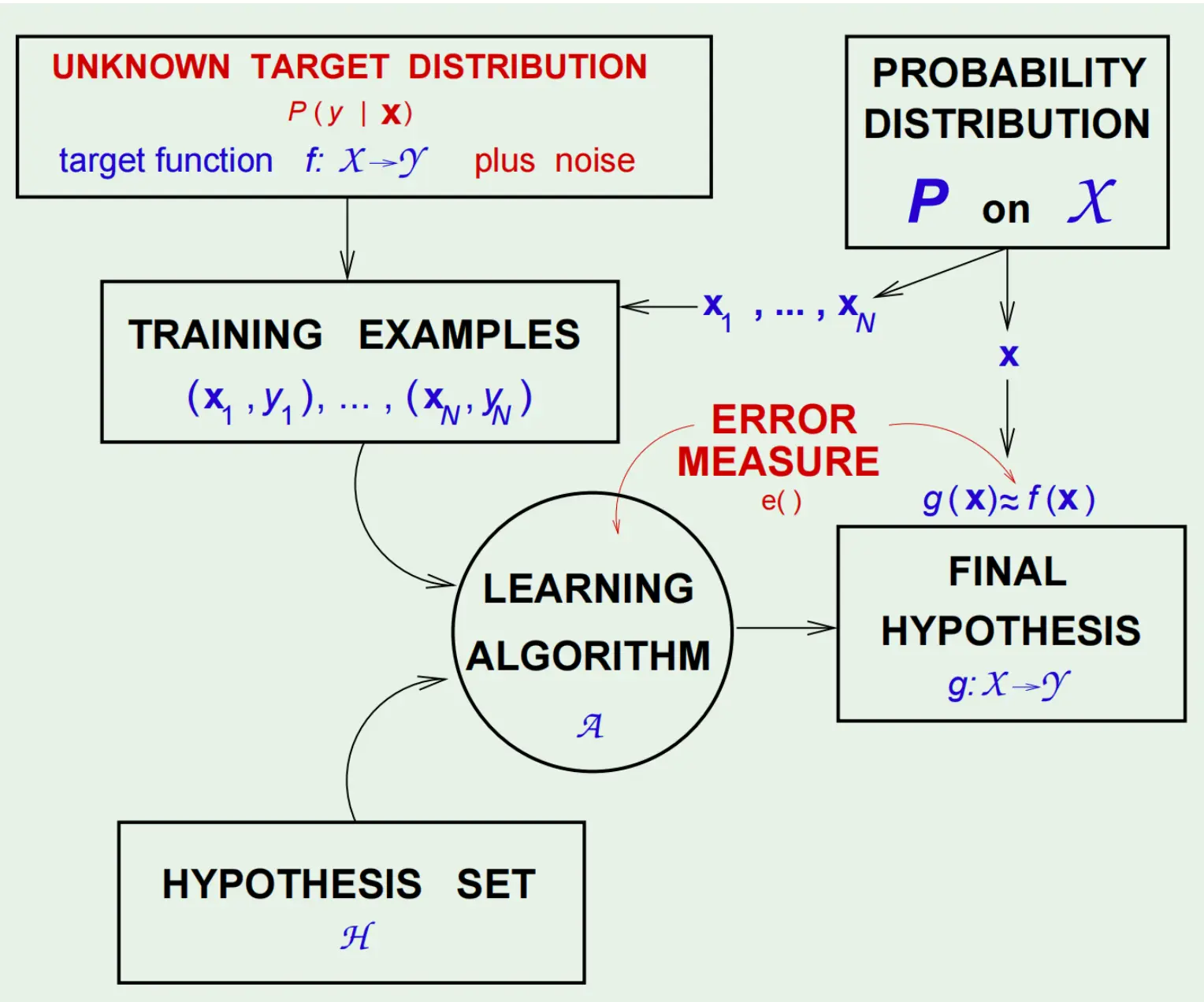： 其中，A用到了e是因为A需要用e来改进学习方向。

在这个框架下，我们尝试去进行BV分析。 我们首先给目标函数加一个噪音，0对称。

$$f(\mathbf{x})⟵f(\mathbf{x})+ϵ(\mathbf{x}),$$$$\begin{array}{r}\mathbb{E}[ϵ(\mathbf{x})]=0\text{(meaning that the noise is zero-mean)}\end{array}$$$$ϵ\sim \mathcal{N}(0,{\sigma }^2)$$

那么和上面一样：

$${\mathbb{E}}_{\mathcal{D},ϵ}[(g^{(D)}(\mathbf{x})-(f(\mathbf{x})+ϵ(\mathbf{x})){)}^2]$$$$={\mathbb{E}}_{\mathcal{D},ϵ}[(g^{(D)}(\mathbf{x})-\bar{g}(\mathbf{x})+\bar{g}(\mathbf{x})-f(\mathbf{x})-ϵ(\mathbf{x}){)}^2]$$$$={\mathbb{E}}_{\mathcal{D},ϵ}[{(g^{(D)}(\mathbf{x})-\bar{g}(\mathbf{x}))}^2+{(\bar{g}(\mathbf{x})-f(\mathbf{x}))}^2+{(ϵ(\mathbf{x}))}^2]$$

拆成三项就是：

$$\begin{array}{rl}& ={\mathbb{E}}_{\mathcal{D},\mathbf{x}}\left[{(g^{(D)}(\mathbf{x})-\bar{g}(\mathbf{x}))}^2\right]+{\mathbb{E}}_{\mathbf{x}}\left[{(\bar{g}(\mathbf{x})-f(\mathbf{x}))}^2\right]+{\mathbb{E}}_{\mathbf{x},ϵ}[ϵ(\mathbf{x}{)}^2]\end{array}$$$${\mathbb{E}}_{\mathcal{D},ϵ}[(g^{(\mathcal{D})}(x)-y{)}^2]=\underset{\mathrm{Variance}}{\underbrace{{\mathbb{E}}_{\mathcal{D},x}[(g^{(\mathcal{D})}-\overline{g}{)}^2]}}+\underset{{\mathrm{Bias}}^2}{\underbrace{{\mathbb{E}}_x[(\overline{g}-f{)}^2]}}+\underset{\mathrm{Noise}}{\underbrace{{\sigma }^2}}.$$

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update