Week 3 Evolutionary Algorithm Basis

字数

3729 字

阅读时间

16 分钟

EA总述

如果将进化算法归类，那么 进化算法 <- 元启发式算法 <- 启发式算法 <- 随机本地搜索 <- 搜索算法 主要的进化算法有：

遗传算法（Genetic Algorithm, GA）
进化规划（Evolutionary Programming, EP）
进化策略（Evolution Strategies, ES）
差分进化（Differential Evolution, DE）

EA的独特之处在于，它是以种群（Population）为单位进化的。本质上是一种随机局部搜索优化算法

举个例子，什么叫以种群进化

假如我们得到了优化问题的封闭表示：$$ f(x) = -{(x-5)}^{2} + 25 $$ 那么我们一开始维护 [2, 7, 1, 6, 4] 计算适应度，就是f(2) = 16, f(7) = 16, f(1) = 4, f(6) = 24, f(4) = 24 我们选择top 4 [6, 4, 7, 2] （适应度高的个体更可能被选中） 然后交叉互换 [6, 4] → 交叉 → [5, 5] （新个体） [7, 2] → 交叉 → [5, 4] （新个体）新种群就是 [5, 5, 5, 4] 然后变异一下，4变成5了就是[5, 5, 5, 5] [5, 5, 5, 5] （所有个体都收敛到 x = 5）最终找到最优解 x = 5, f(5) = 25。

术语总结

Mutations 突变
Crossover 交叉互换
Representation 表示，也就是个体 (Individual) 的一种Encode
Fitness Function 适应度函数 f(x): 有点像Cost Function
Variation Operators 变异算子: 包含 Mutations, Crossover。这些变异算子应用于基因型。
Selection and Reproduction 选择和繁殖: 适应度高的个体更有可能被选中并繁衍下一代。
phenotypes 表现型，也就是f(x)中的x。表现型由基因型决定。
genotypes 基因型，也就是Encode(x)。在计算适应度的时候，如果g为基因型，那么：适应度 = f(Decode(g))

其实就是寻找全局最优，在探索和挖掘中做取舍。交叉互换和突变用于探索，选择和繁殖用于挖掘。

通用框架

Representation

Representation是一种Encode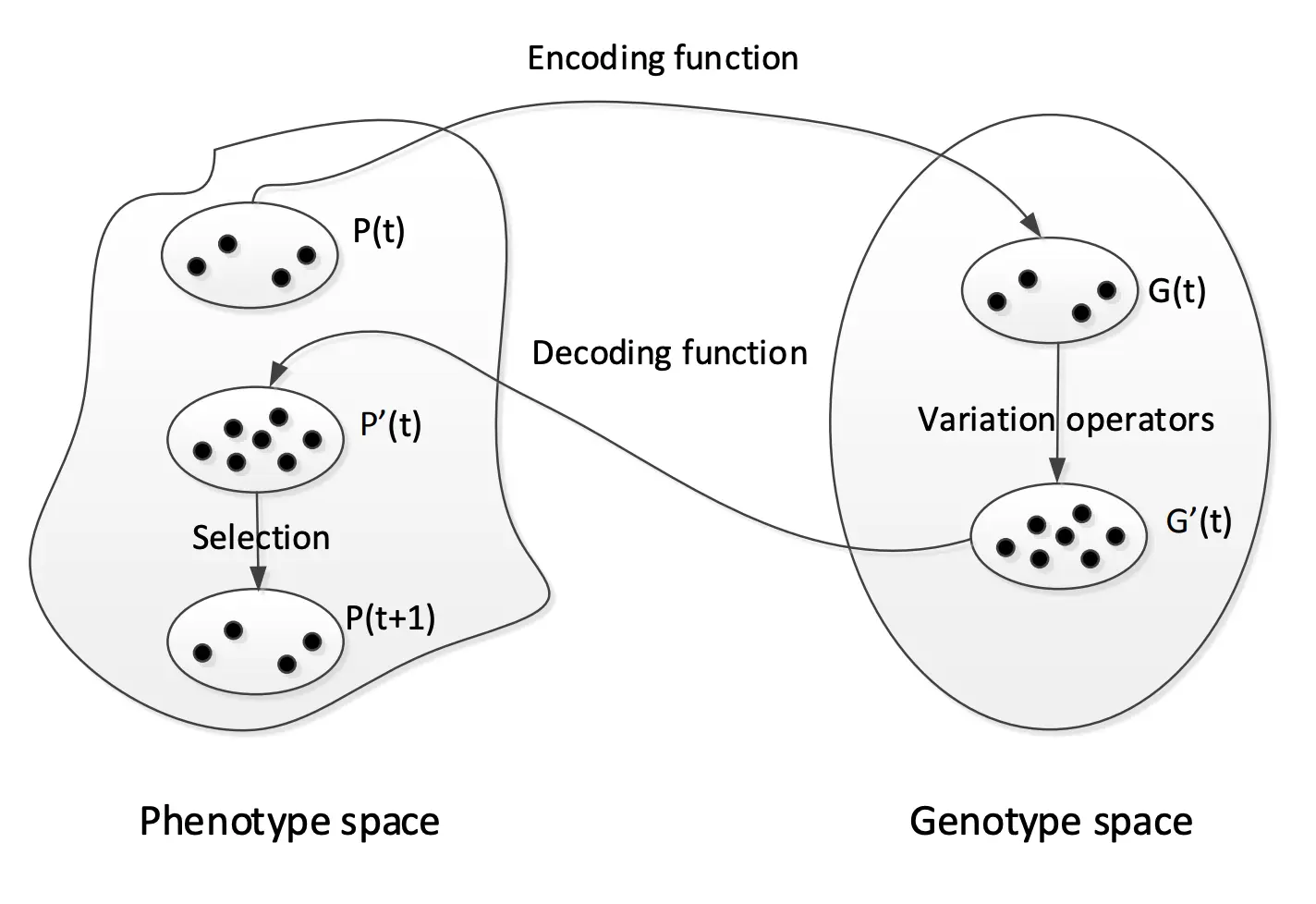

Binary Representation

最传统的Encoder。编码和解码的方式比较像数电模电转换。怎么做这一点呢？举个例子。比如说，你原来的基因型为110100011111，一共12位，而你的目标表现型x = {x1, x2, x3} 3个分量，每个分量xn的定义域为-5到5。那么，由于12位基因型要对应到3个分量，所以每个分量对应4位。 x1 -> 1101。二进制4位能表示15个数，放缩到-5到5，就是 -5 + 13/15 * 10 = 3.6666666667 x2 -> 0001。-5 + 1/15 * 10 = -4.3333333333 x3 -> 1111 = 5 所以表现型就是

优点：模式识别与隐性并列性

首先介绍Schema，这玩意就是模式。比如说10110110和00100100可以被表示为schema *0**01**0 或者 *****01**

二进制encoding的优点就是，由于其把表现型转化为这么细粒度的表示，所以如果有模式体现出来，那么很容易就能被人发现。那么怎么被人发现呢？这就是隐性并列性。

一个长度为 L 的染色体 包含最多 3L^3 个不同的 Schema（因为每个位置可以是 0、1 或 *）。
一个种群中有 MMM 个个体，意味着算法实际上在并行评估 M×3^L 个 Schema。
自然选择 会倾向于保留更优的 Schema，而较差的 Schema 逐渐消失。
进化过程中，我们不仅仅优化个体，也在优化 Schema 结构。

缺点：Hamming Cliff

很简单，就是基因型只突变一位，而表现型差距过大。就比如原本基因型是000，表现型就是0，而如果突变最高位，表现型就是4，突变最低位，表现型就是1。这不好，我们希望差距不要这么大。解决方案：Gray encoding

缺点：冗余表示

如果表现型的定义域不是[0,3]，而是{0和2和3}，那么你需要用同样长的基因型表示。

缺点：精度差

这很简单，数电精度不如模电。

Real-valued vector representation

想法：我们能不能不要encode，decode，直接让基因型与表现型统一？可以。染色体中的每个基因表示问题的一个变量。精度不受编码/解码函数的限制。进化策略（Evolution Strategies）、进化规划（Evolutionary Programming）和差分进化（Differential Evolution）这些都是基于实值进行的。

x = [x_{1}, x_{2}, \dots, x_{n}] \in R^{n}

突变规则

Uniform mutation

在上下界中随机生成一个数代替原位

Non-uniform mutation

c_{i}^{'} = {\begin{cases} c_{i} + Δ (t, v_{i} - c_{i}) & if τ \geq 0.5 \\ c_{i} - Δ (t, c_{i} - u_{i}) & if τ < 0.5 \end{cases}

其中t是当前进化代数。v和u是上下界， $τ$ 是个0到1的随机数，而delta的计算如下：

Δ (t, y) = y (1 - r^{(1 - t / g_{m})^{b}})

r是个0到1的随机数，gm是最大进化代数，b是个控制变异幅度的超参数。早期t小的时候变异幅度delta就大一点，善于探索，后期就小一点，善于挖掘。

Gaussian mutation

生成一个以原位为均值，方差为sigma的新值代替原位，如果超越了bound，就用bound。这里sigma一般用 (上界-下界) / 10

c_{i}^{'} = min (max (N (c_{i}, σ_{i}), u_{i}), v_{i}),

交叉互换规则

Flat crossover

每个 hi 是在 [xi_1,xi_2] 区间内随机选择的值。

Simple crossover

选择一个随机交叉点，然后交换该点之后的所有变量。

Whole arithmetical crossover

计算每个变量的线性组合，alpha是随机数

\begin{array}{r} h_{i}^{[1]} = α x_{i}^{[1]} + (1 - α) x_{i}^{[2]} \\ h_{i}^{[2]} = α x_{i}^{[2]} + (1 - α) x_{i}^{[1]} \end{array}

Local arithmetical crossover

和 Whole Arithmetical Crossover 类似，但每个变量的 α是不同的（α变成一个向量）。

Single arithmetical crossover

随机选择一个变量，用两个父代该位置的平均值替换。
其他变量保持不变。

BLX-alpha crossover

在区间 $[h_{min} - l \cdot α, h_{max} + l \cdot α]$ 之间随机选一个值，允许offspring超出父代区间范围。

Random key representation

没讲

Permutation representation

没讲

Variation Operators

Mutation

对于二进制encoder，就是以一个概率去翻转一位。标准的基因突变概率位 1/L, 但是也可以是1/L到1/2左右闭区间的一个概率。比如说，一个00101011的个体，可以突变成0 (1) 1010 (0) 1

Crossover

随机选择两个parents以pc <- [0,1]的概率进行交叉互换

1-point crossover：在两个基因串上选择一个单交叉点，交换该点之后的数据。
- Parent 1: 11001011
- Parent 2: 00110100
- Offspring 1: 1100 + 0100 = 11000100
- Offspring 2: 0011 + 1011 = 00111011
n-point crossover：在两个字符串上选择多个交叉点，使用这些点将字符串分割成部分，在两个父字符串之间交替，然后粘合部分
- Parent 1: 11001011
- Parent 2: 00110100
- Offspring 1: 110 | 10 | 00
- Offspring 2: 001 | 30 | 11
Uniform crossover：逐位（bit-wise）进行交叉，每一位随机选择来自父代 1 还是父代 2。
- Parent 1: 11001011
- Parent 2: 00110100
- 投掷硬币（50% 概率选择 Parent 1 或 Parent 2）。
- Offspring 1: 10111001
- Offspring 2: 01000110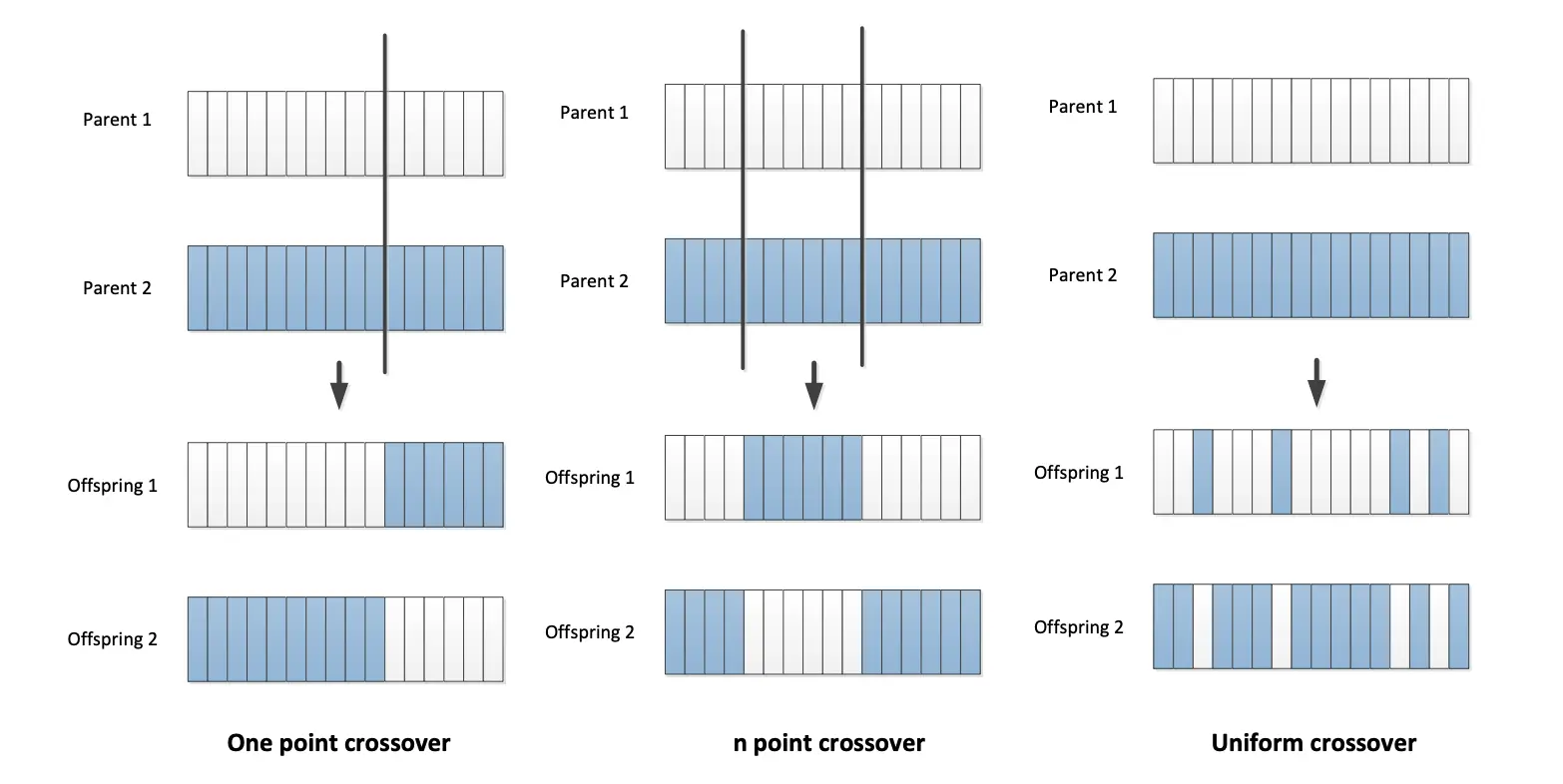

Selection

选择通常在变异运算符之前执行：选择更适合繁殖的个体，选择一个或多个好解决方案的副本。·· 较差的解决方案也会被选择，但机会要少得多

Fitness Proportional Selection

就是轮盘赌。

p_{i} = \frac{f_{i}}{\sum_{j = 1}^{M} f_{j}},

不允许负的适应度值，适应度值较高的个体被淘汰的可能性较小，但仍有可能被淘汰。适应度值较低的个体可能会在选择过程中幸存，允许一些弱个体幸存，这些个体可能有助于逃离局部最优

早期阶段的 "超级个体" 问题

过早收敛（Premature Convergence）
- 超级个体会主导整个种群，导致多样性迅速下降。
- 变异和交叉无法探索更广的解空间，算法可能陷入局部最优（Local Optimum）。
遗传漂移（Genetic Drift）
- 由于超级个体的复制概率极高，许多有潜力但适应度稍低的个体会被淘汰。
- 这导致进化过程失去探索性，减少了进化算法的适应性。

如何解决？用缩放后的适应度值f'替换原始适应度值fi

线性缩放

f_{i}^{'} = a + b \cdot f_{i}

a一般设置为max(f), b一般设置为min(f) / M < 1，M是种群大小

使用缩放的适应性比例选择似乎过于复杂。缩放的本质是什么？在缩放后选择时适应性值其实不重要，我们只想要个排名。

后期阶段适应度分布过于平坦的问题

观察（Observation）：

在进化的后期，所有个体的适应度可能趋于相似，即适应度差异变小。 问题（Question）：没有明显适应度差异会导致什么问题？
选择压力过低（Selection Pressure Too Low）
- 由于个体之间的适应度差别小，选择几乎是随机的，进化停滞。
- 进化算法无法有效区分更优的个体，导致收敛变慢。
缺乏进步（Lack of Progress）
- 由于个体的适应度相似，进化几乎停止，难以找到更好的解。

采用 线性缩放（Linear Scaling） 或 指数缩放（Exponential Scaling） 增强个体之间的适应度差异，保持进化动力。

Ranking Selection

sort之后，不是直接根据适应度值选择个体，而是根据它们的排名（Rank） 来分配选择概率。 p(γ) 是排名函数，用于决定每个个体被选择的概率。

Linear Ranking（线性排名）：
- 线性地分配概率，保证最优个体有更高但不过分的选择概率。

p (γ) = \frac{α + (β - α) \cdot \frac{γ}{M - 1}}{M}

	- **γ 是个体的排名索引**（从 0 到 M−1，其中 M−1 是最优个体）。
	- M是种群大小
	- alpha和beta控制选择压力，约束是a+b = 2
	-  1<= beta <= 2控制排名的力度
	- 最优个体概率为：beta / M
	- 最差个体概率为：alpha / M
	- 通过调整 β，可以控制**最优个体和最差个体的选择差距**
	- 如果让alpha=beta，就成了随机搜索了。

Exponential Ranking（指数排名）：
- 最高排名的个体获得指数级别更高的概率。
- 适用于希望更快收敛的情况。
Power Ranking（幂次排名）：
- 适用于更极端的选择策略，使前几名个体有更大的选择优势。
Geometric Ranking（几何排名）：
- 适用于动态调整选择压力的情况。

Truncate selection：Ranking变种

排名，选择前百分之x 可以被视为最简单的确定性排名选择

Tournament Selection：Ranking变种

设置锦标赛容量为k
随机地从种群中选出P' 这个子集参加锦标赛，容量为k
选出这个子集中适应度最高的
重复直到offspring足够这基本是最受欢迎的方法，k=2经常被使用

(µ + λ) and (µ, λ) selection：Ranking变种

(µ + λ) ：稳定收敛，不易丢失优秀基因，探索性较低，可能陷入局部最优

父代size为µ
从父代中随机选择个体并生成 λ 个子代。
从父代和子代的合并种群（μ+λ个个体）中选取适应度最高的 μ 个个体，形成下一代。

(µ, λ)：促进多样性，避免过早收敛，可能丢失优良个体，收敛不稳定

父代种群大小为 μ。
从父代中随机选择个体并生成 λ 个子代。
从子代中选取最优的 μ 个个体作为新一代。

Selection Pressure

选择压力衡量进化算法（EA）在选择过程中对适应度较高个体的偏好程度。高选择压力 → 强调最优个体（高适应度个体被更频繁地选择）。低选择压力 → 选择更随机，允许适应度较低的个体有更多机会繁殖。

选择压力如何影响开发和探索的平衡？

高压力，强开发，有可能过早陷入local optimum
低压力，强探索，收敛太慢

如何衡量选择压力？

接管时间（Take-over Time, τ）：

定义：初始种群 M 只有一个最优个体 x∗，然后仅执行选择操作（不进行变异或交叉）。
计算：统计需要多少代（τ∗）才能让整个种群都变成 x∗。最优个体会繁殖。
τ∗ 越大，选择压力越低；τ∗ 越小，选择压力越高。

这里有接管时间与各种不同方法的转化方程：

Reproduction

繁殖（Reproduction） 控制如何从当前种群生成下一代。有下面的繁殖策略

Generational EAs（代际进化）

也称为 标准进化算法所有个体都会被更新：

进行变异、交叉生成新个体。
旧种群的个体会被完全替换。
进行新的选择，形成完整的新种群。

Steady-state EAs（稳态进化）

仅用少量（甚至仅 1 个）新个体替换旧个体。
运行方式：
1. 选择少数父代生成子代。
2. 选择较差的个体并用新个体替换。
3. 大部分个体保持不变，种群逐步进化。

精英策略（n-Elitism）

精英主义（Elitism）：确保最优的 N 个个体直接复制到下一代，不会被淘汰。

代际间隙（Generational Gap）

定义：代际之间的重叠程度，即：
- 没有经过变异的个体 在新一代中的比例。
影响：
- 较大代际间隙（低重叠） → 进化变化大，探索性更强。
- 较小代际间隙（高重叠） → 进化更稳定，局部搜索更强。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

Week 3 Evolutionary Algorithm Basis ​

EA总述 ​

术语总结 ​

通用框架 ​

Representation ​

Binary Representation ​

优点：模式识别与隐性并列性 ​

缺点：Hamming Cliff ​

缺点：冗余表示 ​

缺点：精度差 ​

Real-valued vector representation ​

突变规则 ​

Uniform mutation ​

Non-uniform mutation ​

Gaussian mutation ​

交叉互换规则 ​

Flat crossover ​

Simple crossover ​

Whole arithmetical crossover ​

Local arithmetical crossover ​

Single arithmetical crossover ​

BLX-alpha crossover ​

Random key representation ​

Permutation representation ​

Variation Operators ​

Mutation ​

Crossover ​

Selection ​

Fitness Proportional Selection ​

早期阶段的 "超级个体" 问题 ​

线性缩放 ​

后期阶段适应度分布过于平坦的问题 ​

Ranking Selection ​

Truncate selection：Ranking变种 ​

Tournament Selection：Ranking变种 ​

(µ + λ) and (µ, λ) selection：Ranking变种 ​

(µ + λ) ：稳定收敛，不易丢失优秀基因，探索性较低，可能陷入局部最优 ​

(µ, λ)：促进多样性，避免过早收敛，可能丢失优良个体，收敛不稳定 ​

Selection Pressure ​

选择压力如何影响开发和探索的平衡？ ​

如何衡量选择压力？ ​

Reproduction ​

Generational EAs（代际进化） ​

Steady-state EAs（稳态进化） ​

精英策略（n-Elitism） ​

代际间隙（Generational Gap） ​

贡献者 ​

文件历史 ​