Autoencoders and Variational Autoencoders

字数

2242 字

阅读时间

9 分钟

Unsupervised Learning and Autoencoders

如何得到一个数据的有用latent representation? 对于有监督学习，你只需要添加隐藏层，然后把隐层表示映射成标签，并求loss，从而训练。这样自然而然中间的latent vector就是隐藏表示。 然而对于无监督学习，我们没有标签，怎么学出一个latent vector呢？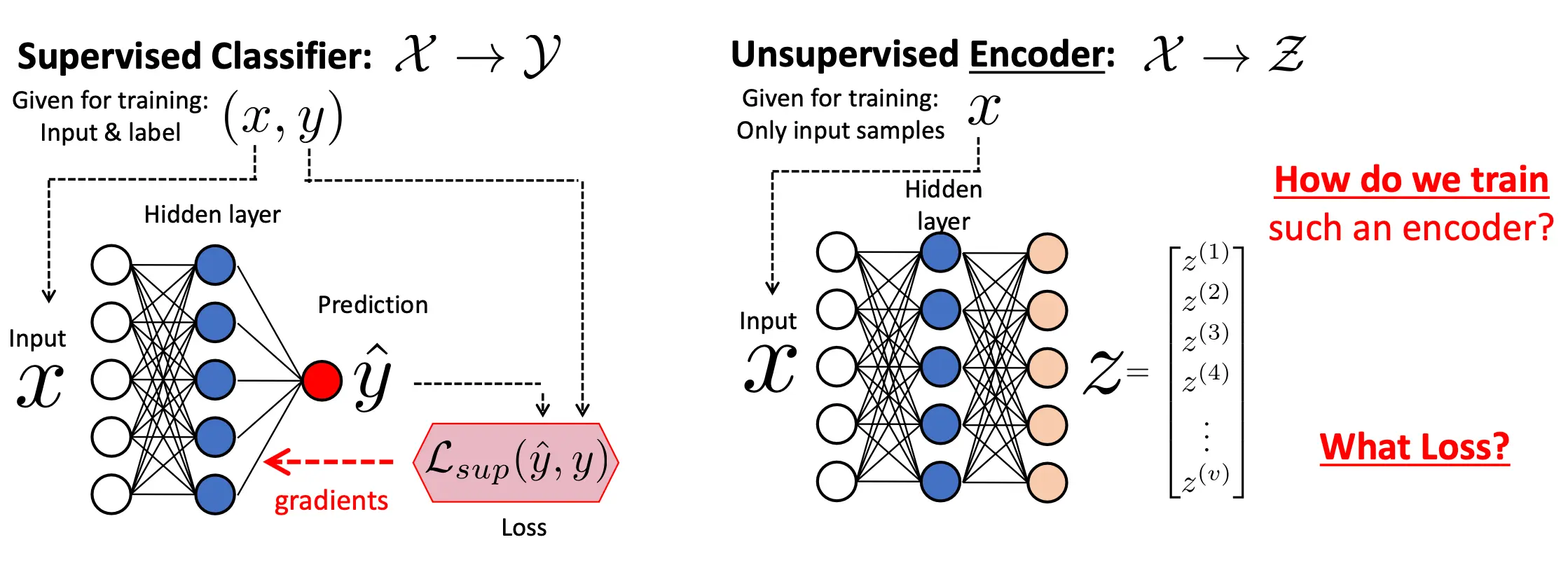

思路就是，我们把输入当成标签，这样再把输入的隐藏层再映射回去，这样就有了隐藏表示。

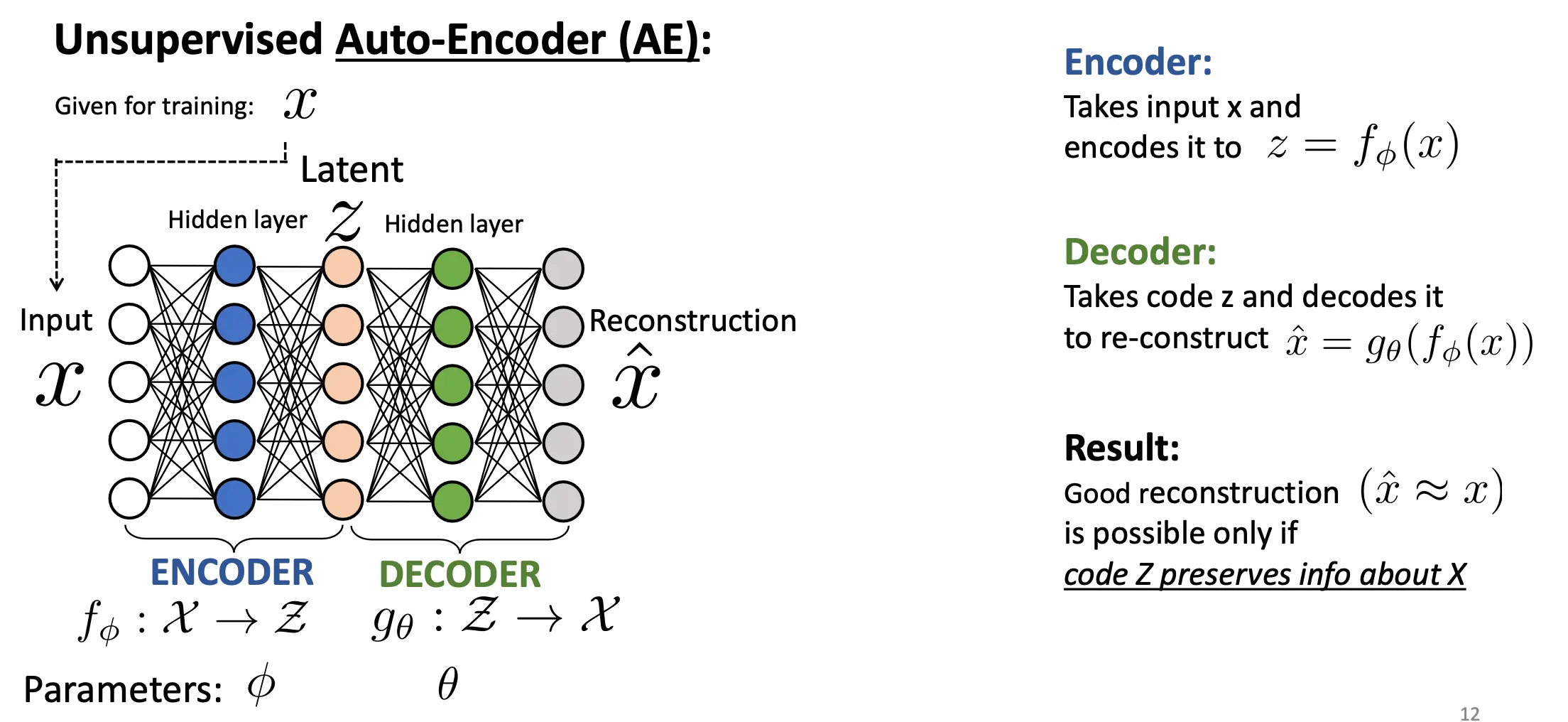
所使用的loss叫做Reconstruction Loss

$$\begin{array}{rl}{\mathcal{L}}_{rec}& \begin{array}{r}=\frac{1}{d}\sum _{j=1}^d(x^{(j)}-{\hat{x}}^{(j)}{)}^2\end{array}\\ & \begin{array}{rl}& =\frac{1}{d}\sum _{j=1}^d{(x^{(j)}-g_{\theta }^{(j)}(f_{\varphi }(x)))}^2\end{array}\end{array}$$

可是这就有问题了。如果f学出来了一个恒等函数，而g也学出来一个恒等函数，这怎么办？加BottleNeck。维度不同自然不能恒等。

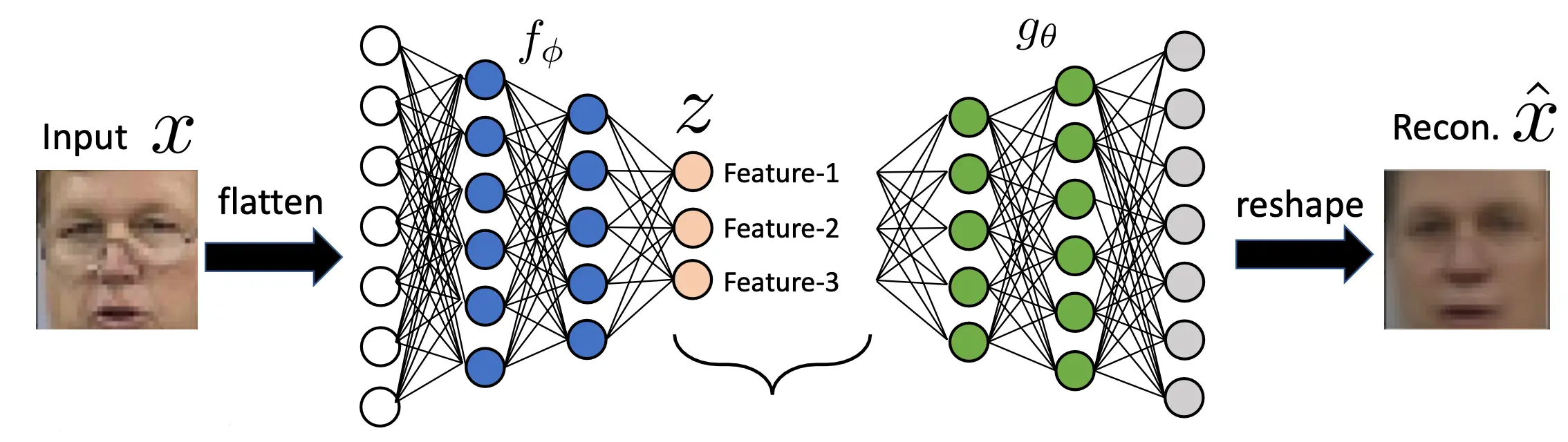
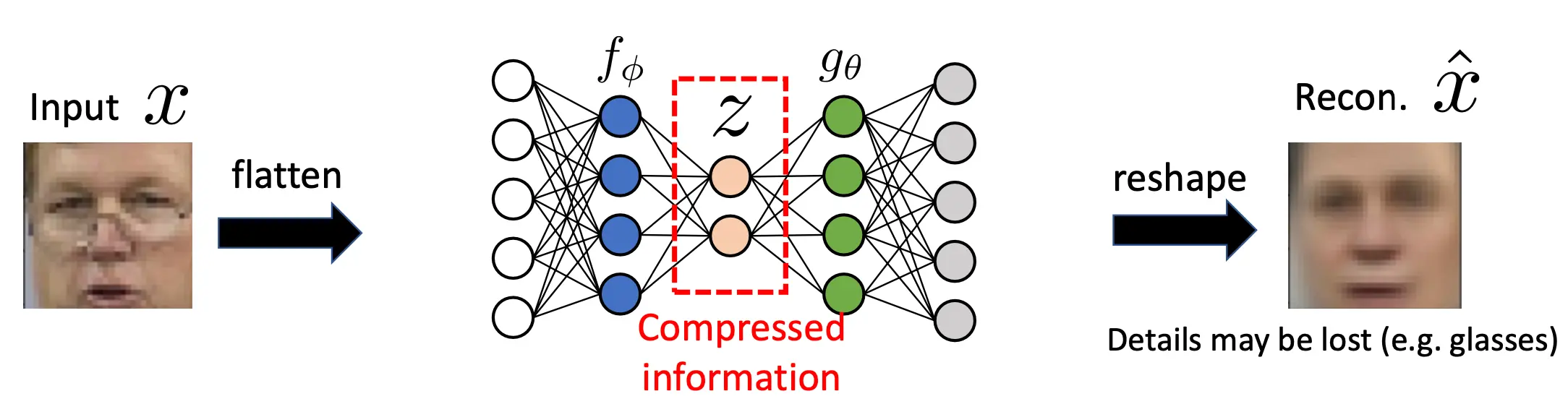然而，这样涉及到了信息的压缩，很多高级的特征并没有被学到。所以如果想要提高重建质量，就应该加深编码器和解码器，以及加宽bottleneck。这是一个trade off。深层次网络能提取到更高级的特征，而更宽的网络能学习到更底层的特征。你需要找好平衡点。

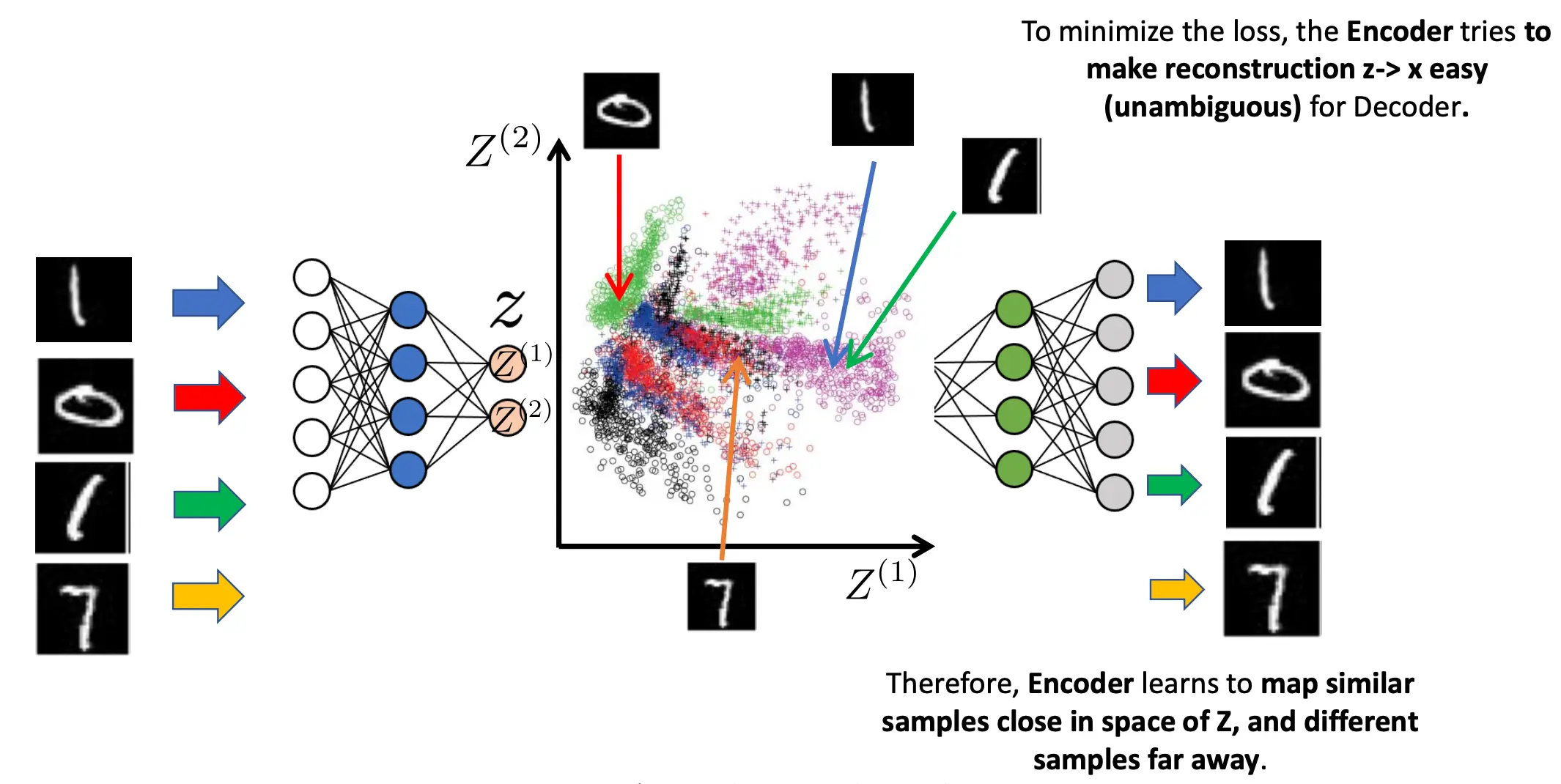
而从mnist数据集上看，autoencoder学习到了如何在Z空间cluster data

还有技巧，就是在有标签的数据比较少的情况下，你可以先pre train一个autoencoder，然后再在后面接一个shallow网络进行有标签训练。 在训练的时候，你可以选择冻结AE的权重，这样的优点是后面的shallow网络很薄，不容易过拟合，但缺点就是AE没有经过标签的优化，你的Ein可能是不理想的。 你也可以选择不冻结AE权重，全部训练。这样的话你可能获得一个更小的Ein，但是你可能会过拟合。你可以选择早停来避免。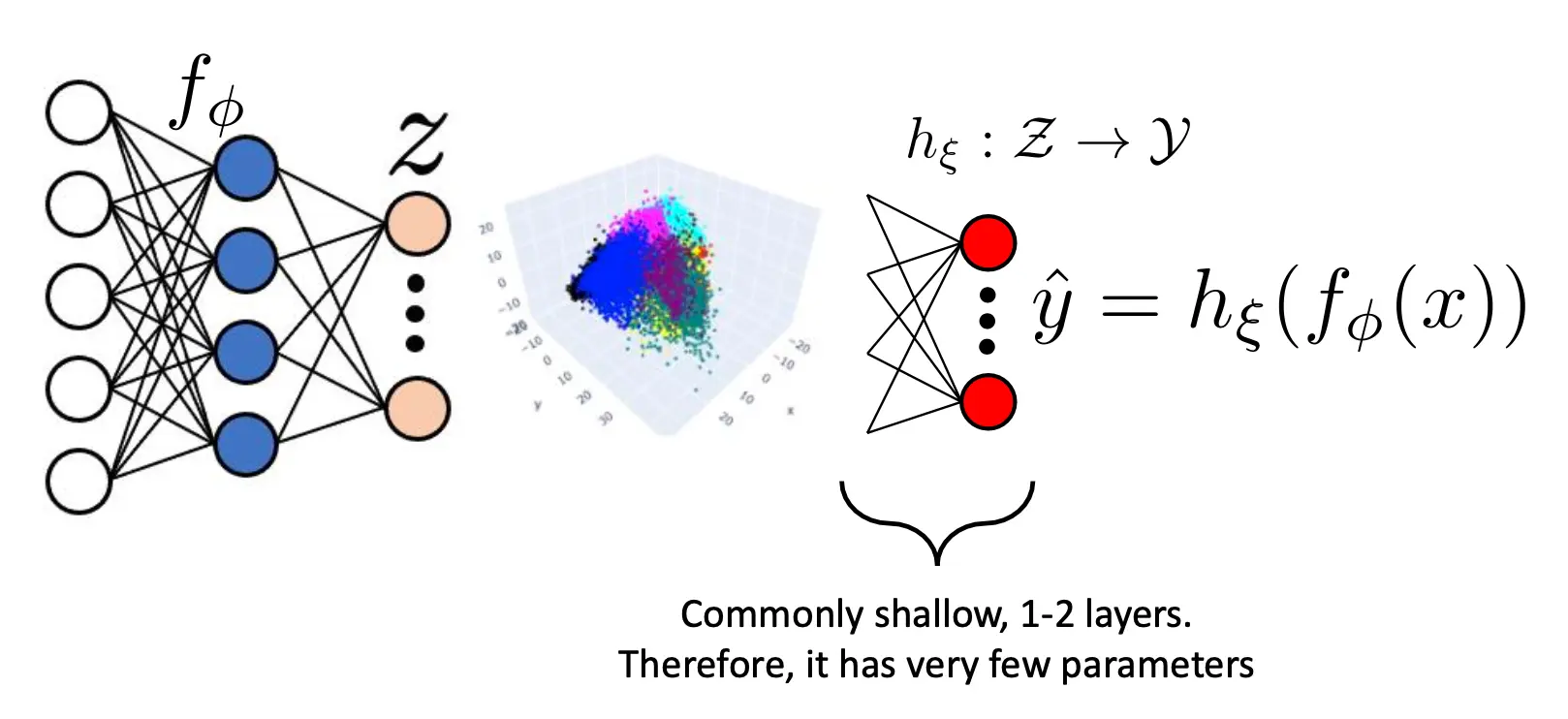

Variational Autoencoders

这是我目前我感觉在可解释机器学习之外设计最棒的网络。

VAE前言理解

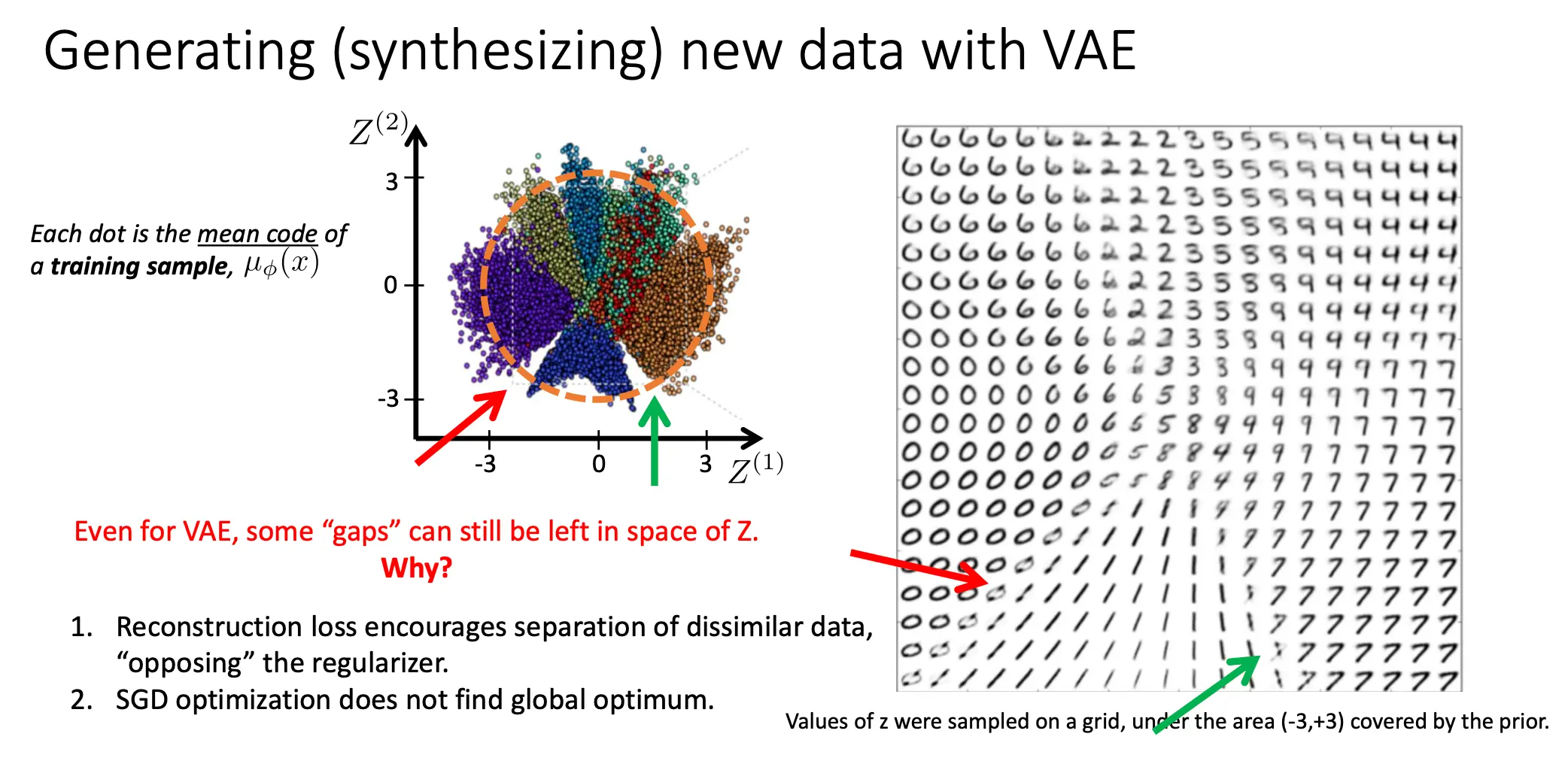
在传统AE中，我们已经猜到，如果单用后半部分解码器，在Z空间中采样，能做到生成任务。 但这大概率是失败的。因为你训练样本都被映射成为了Z空间中的一个一个点，十分稀疏。在实际表现中，如果你在Z空间中采样了非训练样本的点（如图中的红色，绿色点），那么你大概率会得到一个不能看的图。

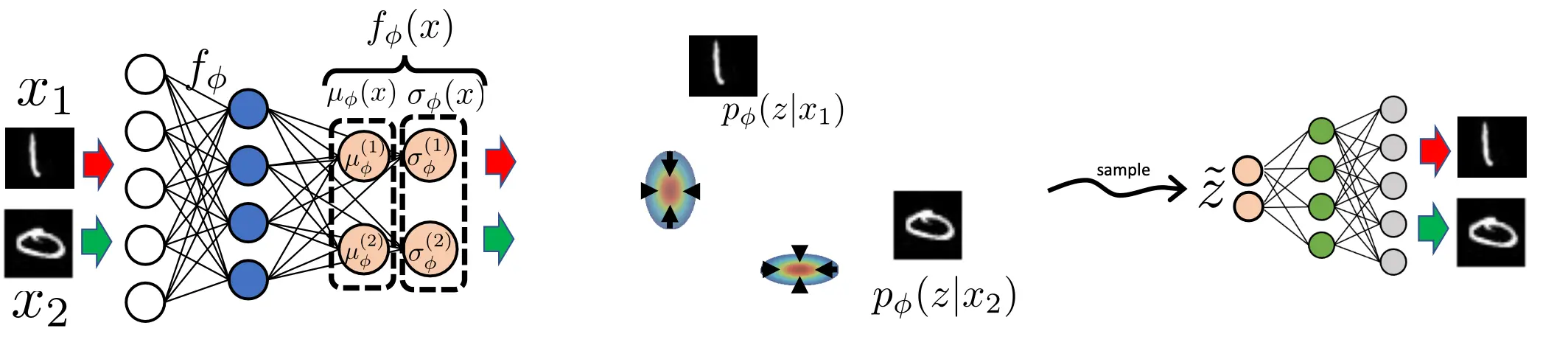
那么我们如何能够解决这个问题呢？VAE诞生了。VAE的主要的想法就是，我不能输出一个点了，而是输出一个分布，意思就是，比如说原来给数字8的图，我映射到Z空间的点是 (0.4, 0.8), 编码器输出的东西是两个值，0.4和0.8，那么我现在修改编码器的输出数量，变成4个值，也就是 ${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2$ 。这样，我们给8图片的时候，编码器编出的东西可能就是 (0.4, 0.2), (0.8, 0.3)，这样就相当于告诉解码器说，我原本给你的是一个点，如果你正好戳在那个点上，我斩钉截铁地告诉你，需要恢复出的图就是8. 可是现在我如果戳到了比如(0.42, 0.83), 在原本的时候，由于没和(0.4, 0.8) 重合，那么解码器就是不认识的，因为没接受过这种点的训练。可是现在，看到(0.42, 0.83)，我解码器就能意识过来，哦，这个东西原来是8的概率是80%，原来是6的概率是13%, 那么我就按照这种成分，生成一个基本像8，可是略微略微像6的图，这样的成功概率就高了。

所以VAE的难点在于，如何让生成出的mu sigma他具备统计学意义，而不是两个随便的数。 有了这样的前置理解，我们接下来进入VAE的设计思路。

VAE具体设计

首先，拿Z空间是一个2维空间举例子。原来输出z1, z2，现在输出z1, z2的概率分布，也就是要输出 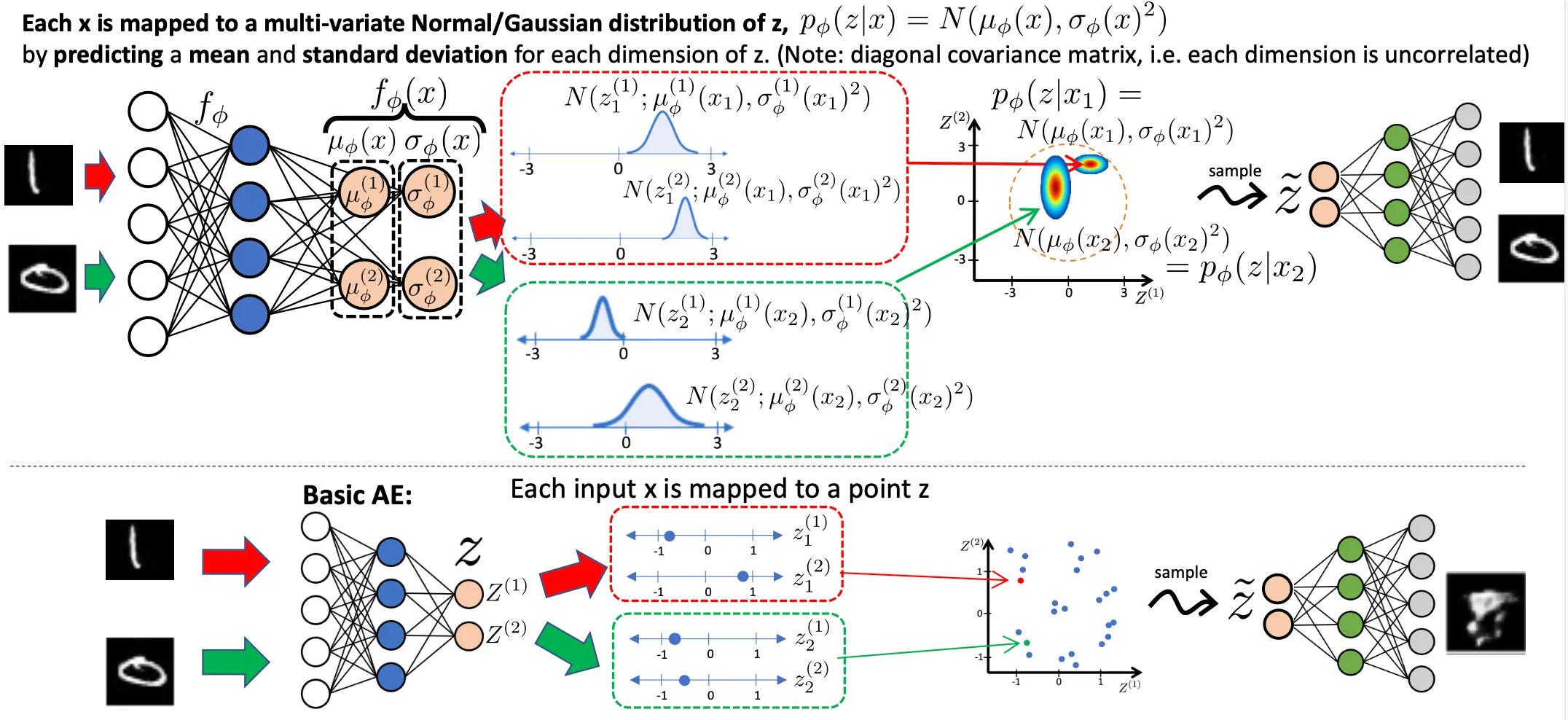${\mu }_1,{\sigma }_1,{\mu }_2,{\sigma }_2$ ,所以现在我们要改中间的两个神经元为4个：

如果思考的比较少的话，其实到这就结束了，因为我们已经改点输出为概率输出。可是这里就面临几个问题：

1. 意义问题：你如何让输出的mu和sigma是有意义的呢？
2. 且你如何限制sigma是个正数？
3. 重叠问题：如果你学出来的重叠太多，当你采样到某个点的时候，到底算1还是6？（如图x1是1，x2是6）

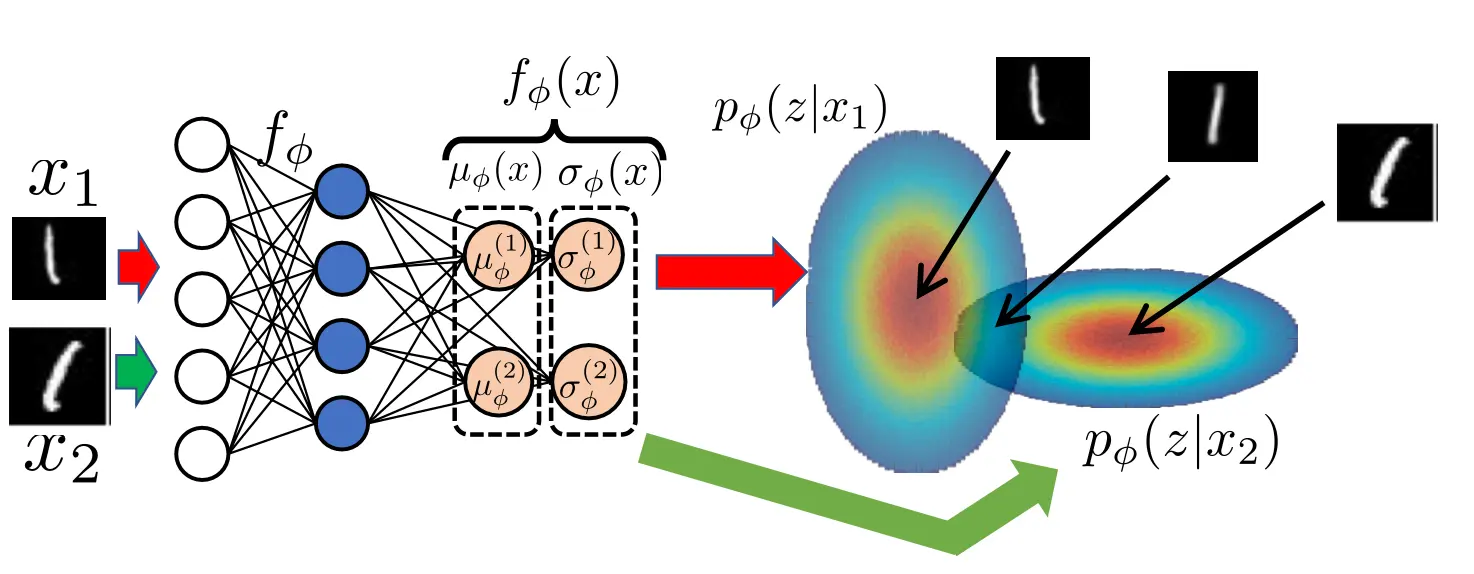
首先我们先来解决问题2，如何确保sigma是个正数。这比较简单。我们只要treat原本想要让输出sigma的神经元的输出为log(sigma)就行。这样当我们想用的时候，我们只需要对这个输出求exp就可以。这样输出的sigma肯定是正数。问题2解决。

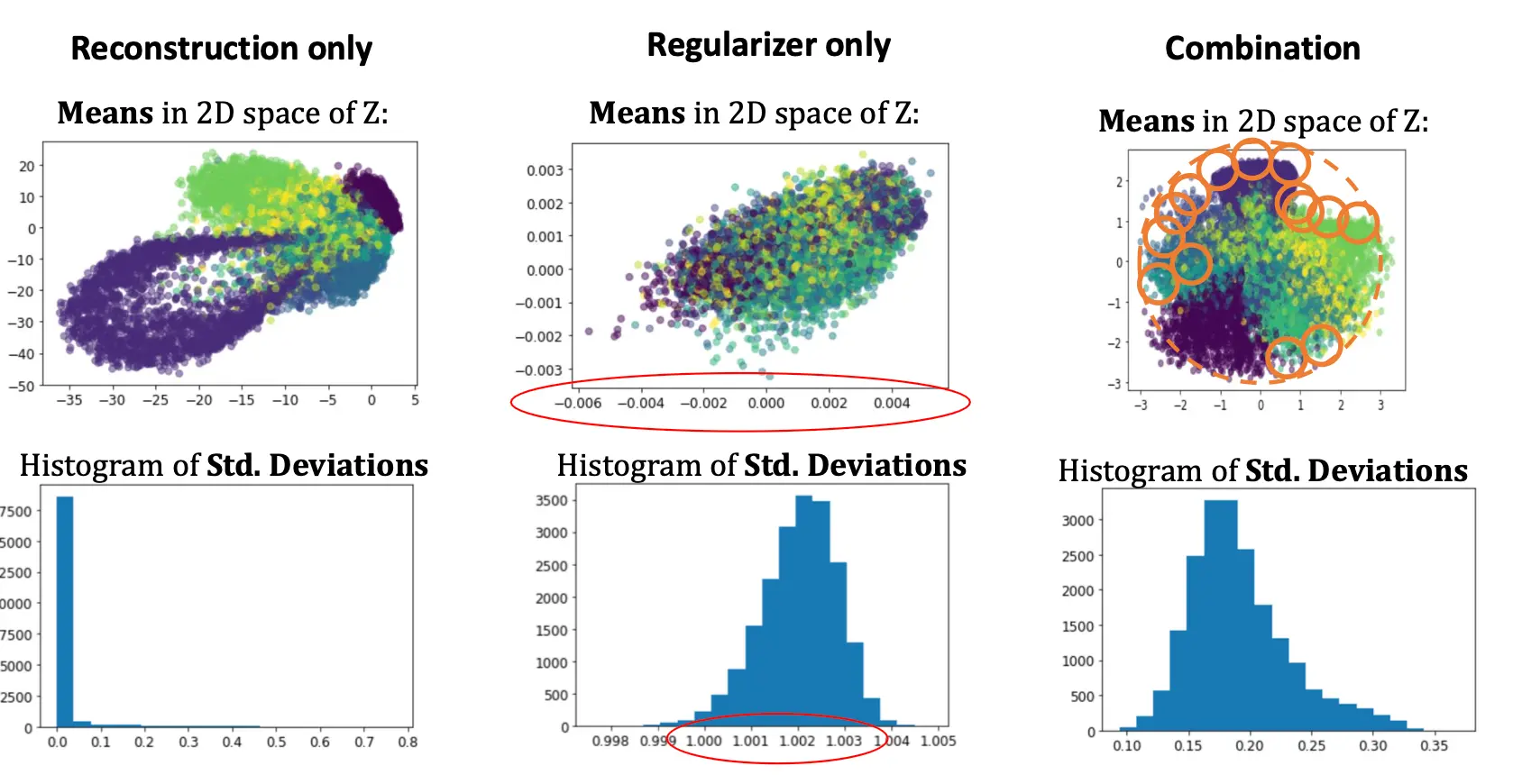
那问题1和3其实是一个共生问题。因为在原本的AE中，我们采用的是reconstruction loss，我们知道，reconstruction loss倾向于让encode出来的东西成为Z空间中的一个单独的点，也就是说，reconstruction loss会使得mu之间互相离得很远，sigma趋向于0.

那么做mu sigma的改进就没有用了。所以我们希望有一个力量，与reconstruction loss相抗衡。reconstruction loss负责拉远分布，另一股力量将分布维持，让学出来的这个分布至少要趋近于正态分布。所以我们设计了这样的Loss：

$$\{{\theta }^{\prime },{\varphi }^{\prime }\}=arg\underset{\theta ,\varphi }{min}{\mathbb{E}}_{x\sim p_{data}}\left[{\mathcal{L}}_{VAE}\right]=arg\underset{\theta ,\varphi }{min}{\mathbb{E}}_{x\sim p_{data}}\left[{\mathcal{L}}_{rec}\right]+\lambda {\mathbb{E}}_{x\sim p_{data}}\left[{\mathcal{L}}_{reg}\right]$$$${\mathcal{L}}_{reg}={\mathbb{E}}_{x\sim p_{data}}{D}_{KL}[p_{\varphi }(z|x)||N(0,I)]=\frac{1}{2}\sum _{j=1}^v[({\mu }_{\varphi }^{(j)}(x){)}^2+({\sigma }_{\varphi }^{(j)}(x){)}^2-2\log {\sigma }_{\varphi }^{(j)}(x)-1]$$

为什么出现了x~pdata? pdata是真实世界中每个样本种类的出现概率分布。算期望的时候就是根据这个概率去乘损失的。 为什么出现了E？其实就是按着pdata对整个batch求平均。因为batch是在data上采样的，所以batch的分布不应该离得data太远。 我们用到了KL散度。KL散度衡量了两个分布的差异。这样的设计可以一定程度上让学出的分布更像一个分布，而不是一个点。 那能不能只用KL散度呢？可想而知没啥用，所有分布都变成0-1高斯了，全重叠到一块去了，VAE更是什么都分不出来。

所以将二者搭配使用，可以将学出的所以分布限缩在一个0-1高斯范围内，且这个高斯范围内不同的块区（不同mu）代表着不同的encode。 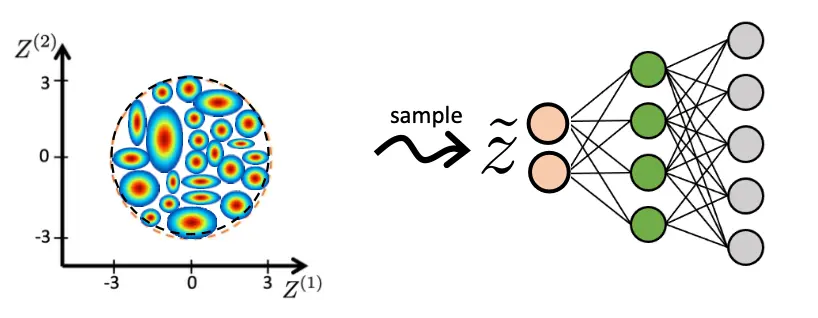真实情况中，就长这样：

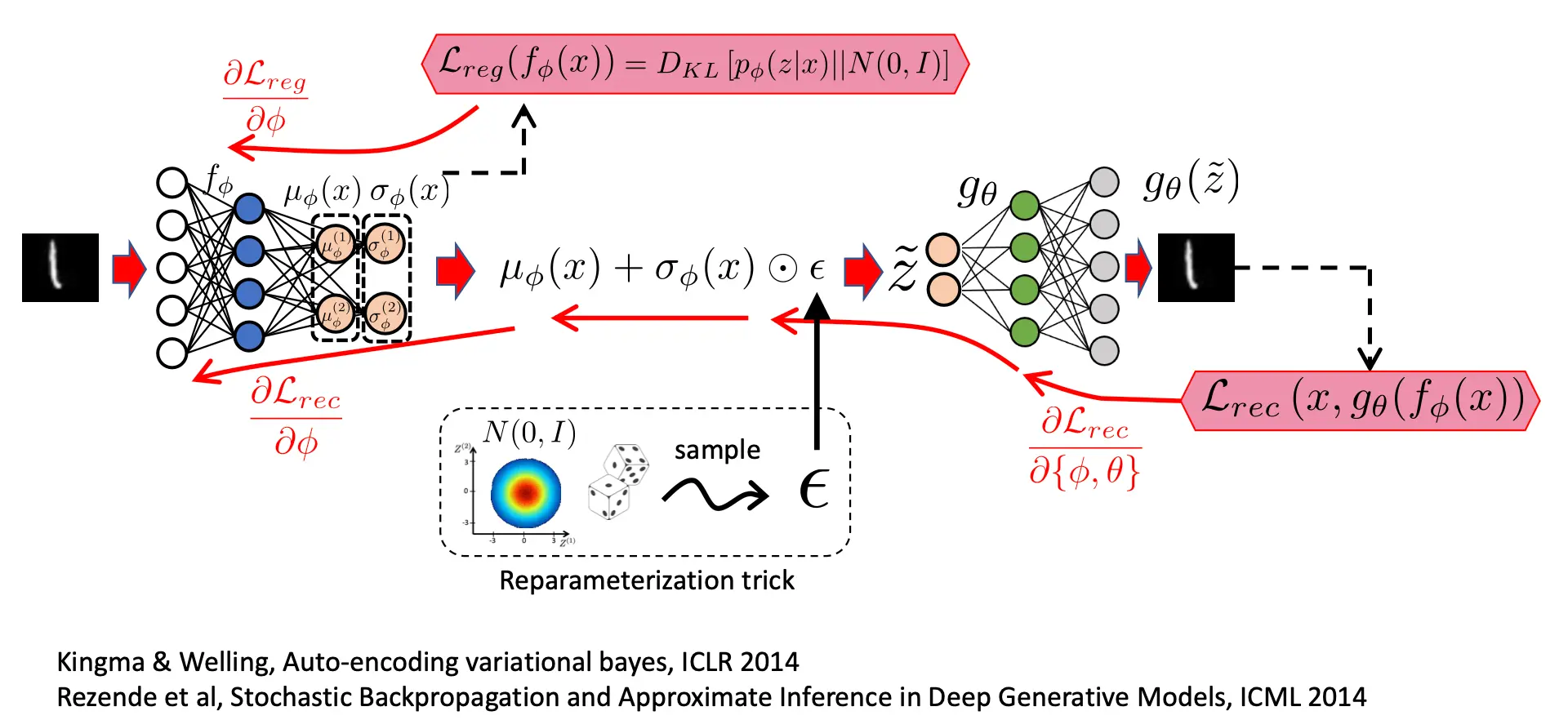
OK现在1和3也解决完了。那问题结束了吗？其实没有。我们还忽略了训练。 如果当你得到分布之后，让计算机随机在上面取一个点z，那么这个过程是不可微的，所以梯度没法反向传播。 你需要选择一种可以微分的方法，那么这个方法就如下所示：

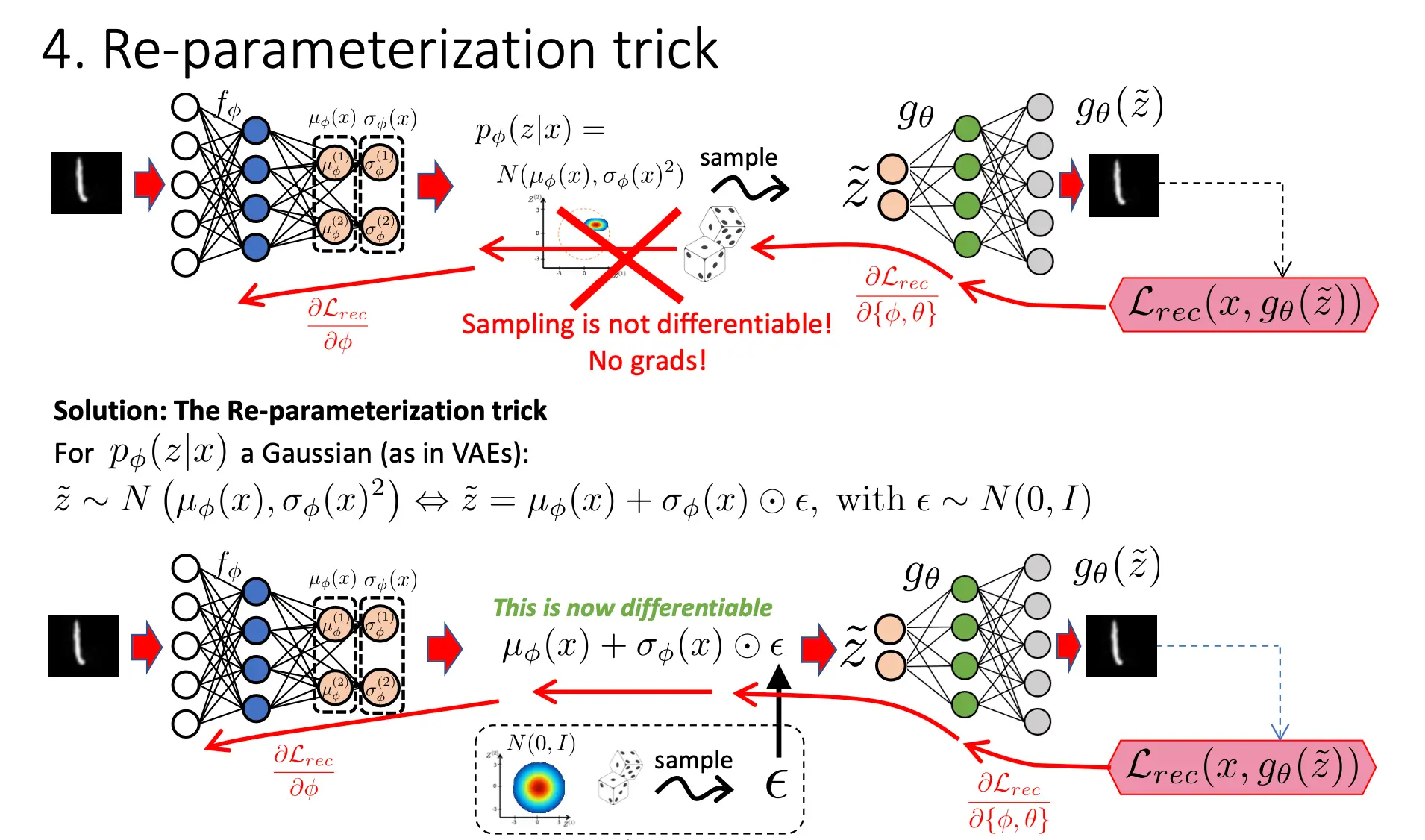
为什么这个过程是可微的呢？因为你采样得来的epsilon在求导的时候会变成常数，从而可微。 整个VAE的梯度流应该是这样的：

VAE的讲解就结束了，下面看一些VAE的成果：

VAE的Loss怎么来的？

我们其实就是想要知道ptheta(x)，也就是真实图像的分布 但我们只知道给定z和x的联合分布，也就是：

$$p_{\theta }(x,z)=p(z)p_{\theta }(x\mid z)$$

我们希望最大化数据的对数边缘似然：

$$\log p_{\theta }(x)=\log \int p_{\theta }(x,z)\mathrm{d}z$$

直观上就是“在我们这个模型（参数为 θ ）下，观测到数据 x 有多大概率”。 而这个积分并不好求，所以我们用Jensens 不等式：

$$\begin{array}{rl}\log p_{\theta }(x)& =\log \int q_{\varphi }(z\mid x)\frac{p_{\theta }(x,z)}{q_{\varphi }(z\mid x)}\mathrm{d}z\\ & \ge \int q_{\varphi }(z\mid x)\log \frac{p_{\theta }(x,z)}{q_{\varphi }(z\mid x)}\mathrm{d}z=\mathcal{L}(\theta ,\varphi ;x),\end{array}$$

其中$$\boxed{\mathcal{L}(\theta,\phi;x)=\mathbb{E}{q\phi(z\mid x)}{\left[\log p_\theta(x\mid z)\right]}\mathrm{~-~KL}{\left(q_\phi(z\mid x)\parallel p(z)\right)}}$$ 这玩意就是我们的Loss，也叫ELBO，Evidence Lower BOund

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update