Week 5 Unsupervised Learning

字数

2988 字

阅读时间

12 分钟

无监督学习是指在无标签的情况下从数据中学习有趣的模式。 其中，聚类算法尝试去识别相似的群组 还会利用一些降维技巧来简化数据，但不使数据失真

Motivation Question

主题分类。 在有标签的情况下，你可以训练一个分类器。当拿到一个新的文章后，你可以用这个分类器来分类新文章。 但是这就涉及到一些问题，一方面是这类标签很贵，另外，如果有新主题的文章，而你的标签库里面没有这个新主题，那么这个文章的分类其实是不好的。 我们把Topic Analysis分为3个子问题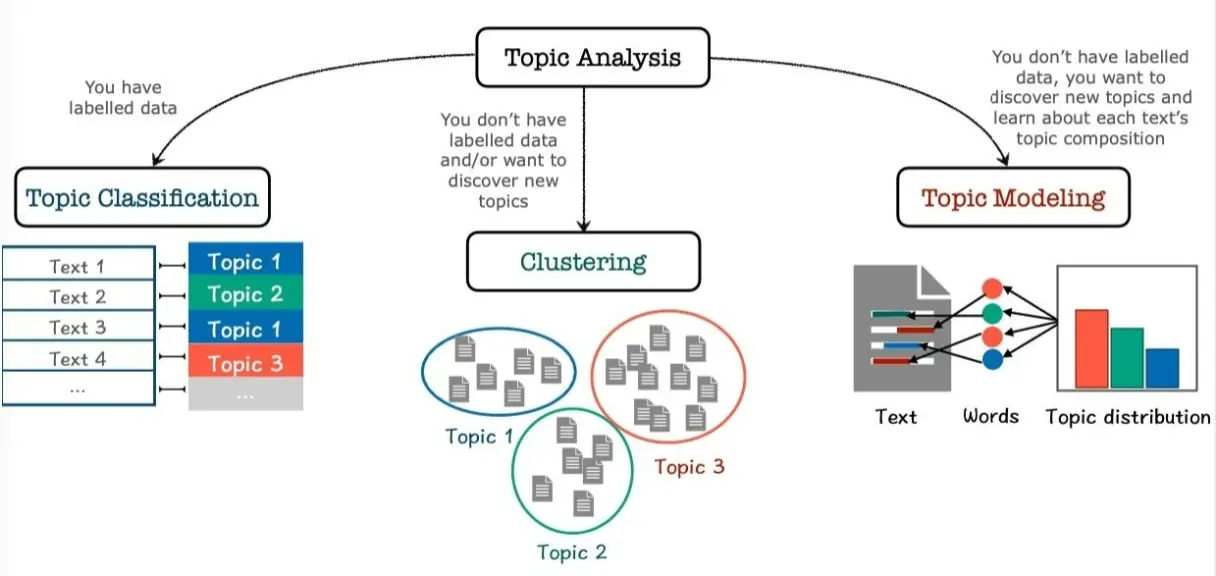： 如果你有标签，那么你就用分类器去分类一个文章 如果你没有标签，你就用聚类算法 如果你没有标签，并且你还想去发现新主题，并了解一个文章属于某个主题的概率，那么就是Topic Modeling任务。

那么这些算法，一般是个什么pipeline呢？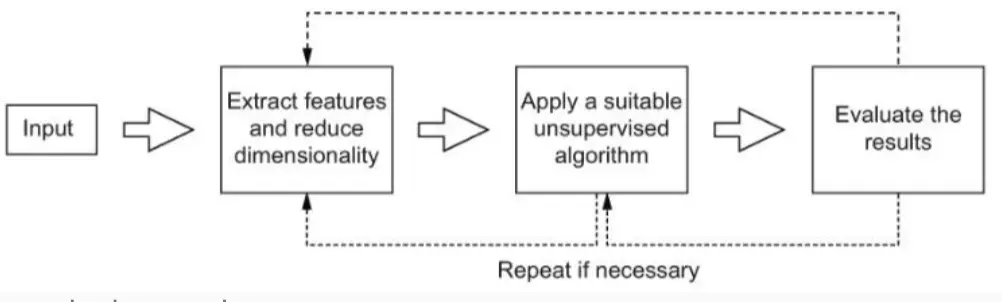

NOTE

1. 输入（Input）：输入的是一组文本数据，例如新闻文章、社交媒体帖子或论文摘要。
2. 特征提取和降维（Extract features and reduce dimensionality）：
   • 文本数据通常是高维的（因为每个单词都可以是一个特征）。
   • 降维的目标是去除噪声、减少计算量，使数据更易于处理。
   • 常用的方法有 TF-IDF、Word2Vec、BERT Embeddings、SVD（奇异值分解）、PCA（主成分分析）、NMF（非负矩阵分解） 等。
3. 应用无监督算法（Apply a suitable unsupervised algorithm）：
   • 由于主题建模是无监督的，常见方法包括：
     • LDA（Latent Dirichlet Allocation）
     • NMF（Non-negative Matrix Factorization）
     • LSA（Latent Semantic Analysis）
   • 这些方法会发现不同文档之间的相似性，从而归纳出潜在的主题。
4. 评估结果（Evaluate the results）：
   • 由于无监督学习没有“正确答案”，评估通常依赖于可解释性（例如查看主题词的合理性）。
   • 可能需要反复调整参数（如主题数量）。

💡 循环部分（Repeat if necessary）：意味着如果结果不好，可能需要重新进行特征提取或调整算法参数。

Clustering

K-means clustering

NOTE

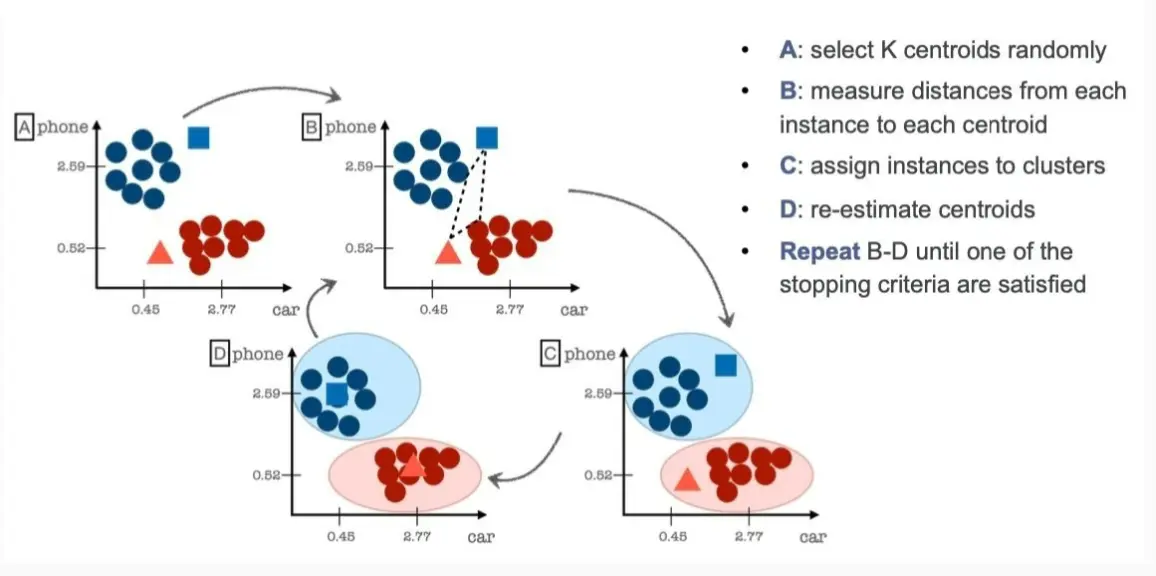
A) 选择 K 个随机质心（centroids）

• 质心是 K-Means 聚类的核心，每个簇的中心点。
• 在步骤 A，算法随机选择 K 个数据点作为初始质心（如图中蓝色方块和红色三角）。

(B) 计算每个点到质心的距离

• 计算所有数据点到当前质心的距离（常用欧几里得距离）。
• 例如，图中数据点计算自己到两个质心的距离。

(C) 分配数据点到最近的质心

• 每个数据点被分配到离它最近的质心，从而形成 K 个簇。
• 例如，图中红色点靠近红色三角，所以被分配到红色簇，蓝色点靠近蓝色方块，所以被分配到蓝色簇。

(D) 更新质心

• 计算每个簇的新质心（通常是簇内所有点的均值）。
• 例如，图中蓝色方块和红色三角的位置会随着簇的变化而调整。

(E) 重复 B-D，直到满足停止条件

• 可能的停止条件：
  1. 质心位置不再发生变化。
  2. 数据点的分配不再变化。
  3. 达到最大迭代次数。

那么如何选择最优秀的K呢？

Elbow Method

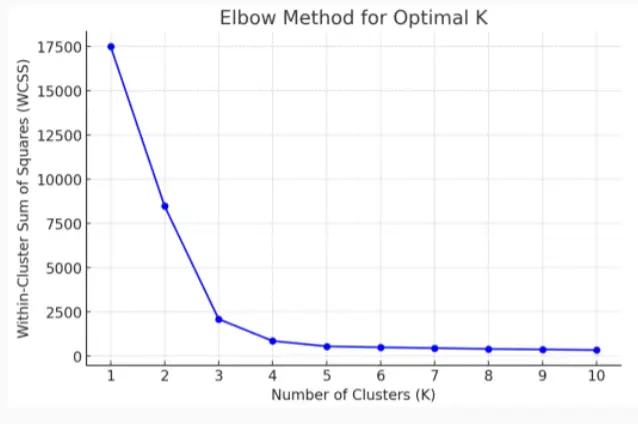选择4

Silhouette Score 轮廓系数

轮廓系数衡量了簇内紧密性（cohesion） 和簇间分离度（separation），定义为

$$S=\frac{b-a}{max(a,b)}$$

a = 点到同簇内其他点的平均距离（越小越好）。 b = 点到最近邻簇的平均距离（越大越好）。 S为-1到1，越接近1说明越好。 理想范围：0.5 到 1（数值越高，聚类质量越好）。选择最高轮廓系数对应的K

Dimensionality Reduction

如果一个向量维度过高，那么在k-means里面计算距离代价很高。 而且如果一个向量很稀疏，那不好。 解决方法有一个就是去除掉高频次，比如the a之类的 另一个方法就是SVD奇异值分解。其中应用于文本中的方法为LSA（Latent Semantic Analysis）

SVD

通过将一个矩阵分解为3个较小的矩阵来简化计算。你把三个矩阵乘起来就能得到原来的矩阵。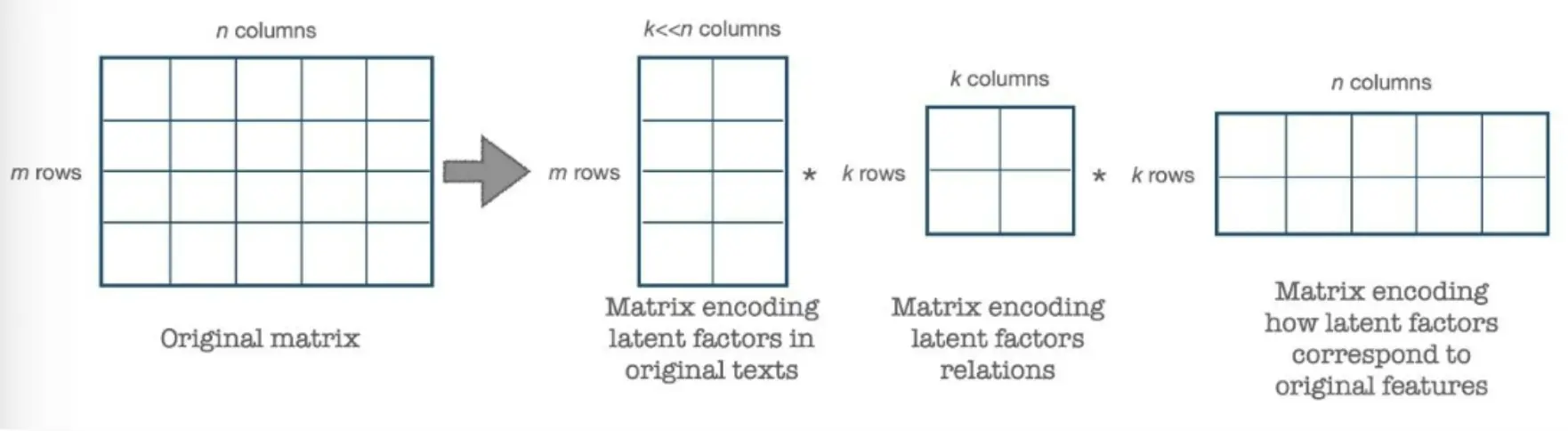

$$A_{m\times n}=U_{m\times k}\cdot S_{k\times k}\cdot V_{k\times n}^T$$

A为原始矩阵，U为左奇异矩阵，表示文本与主题（latent factors） 之间的关系，S为对角矩阵，表示每个主题的权重，V为右奇异矩阵，表示主题与单词（原始特征） 之间的关系。 至于数学上如何分解，是一个固定的流程，这里不介绍了。 如果想要再次降低矩阵的维度，可以选择前k个最大的奇异值，这就是低秩近似。

Evaluating Clustering Algorithms

• 内部评价标准：
  • 依赖于空间（space）和距离度量（distance metrics），如欧几里得距离、余弦相似度等。
  • 轮廓系数（Silhouette Score），簇内误差平方和（WCSS，Within-Cluster Sum of Squares）：用于 Elbow Method 选择最佳 K 值。
• 下游任务评价
  • 信息检索的速度，实用性
• 外部评价标准
  • 如果数据有标签（如文本分类任务），可以检查聚类结果是否与已有类别匹配。
  • Purity，Homogeneity，Completeness，V-measure这些指标都属于 外部评估指标（External Evaluation Metrics），用于衡量聚类结果与真实类别（ground truth）之间的一致性。 它们主要用于有已知类别标签（labeled data）的数据集，可以比较聚类算法的性能。

Purity

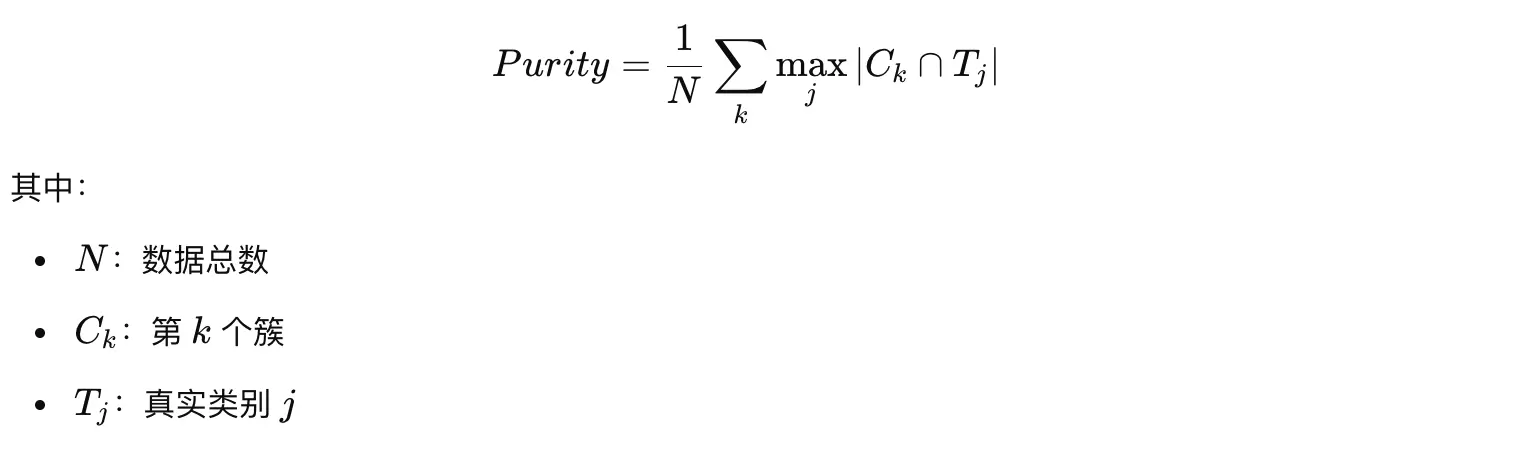
1. 确定每个簇的主类别（majority label），即该簇内出现最多的真实类别。
2. 统计该类别的样本数，作为正确分类的样本。
3. 计算所有簇中正确分类的样本占比，得到 Purity 值。

Homogeneity（同质性）

如果每个簇只包含单一真实类别的数据点，则聚类具有同质性 越大越好。

Completeness（完整性）

如果某个类别的所有数据点都被分配到同一个簇，则聚类具有完整性

V-measure

V-measure 是 Homogeneity 和 Completeness 的调和平均数.兼顾簇的纯度（Homogeneity）和类别的完整性（Completeness），相比单独使用某一指标，更加稳定。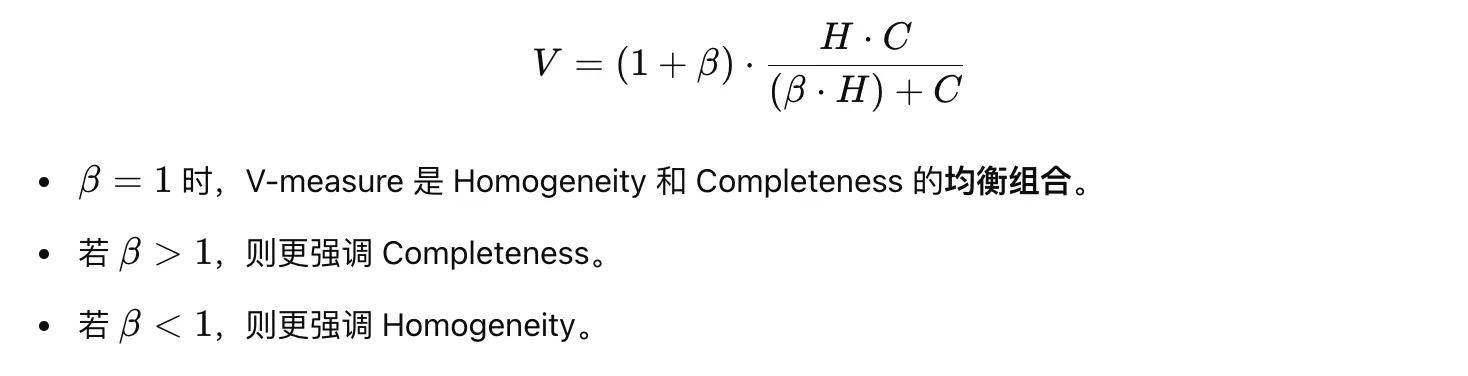

Topic Modelling

如果你是一个编辑，考虑用ML方法来分类，那么你应该这样选择：

• 如果有高质量的标注数据，可以使用 文本分类（Supervised ML） 来自动化新闻分类。
• 如果需要发现新话题，可以使用 无监督学习（Unsupervised ML），例如 LDA 主题建模 或 聚类（K-Means）。LDA可以发现新出现的潜在主题，K-means只能发现新主题但是给不出主题词。
• 如果文章可能涉及多个话题，可以使用 LDA 来获取 主题概率分布，让文章归类更加灵活。

Latent Dirichlet Allocation

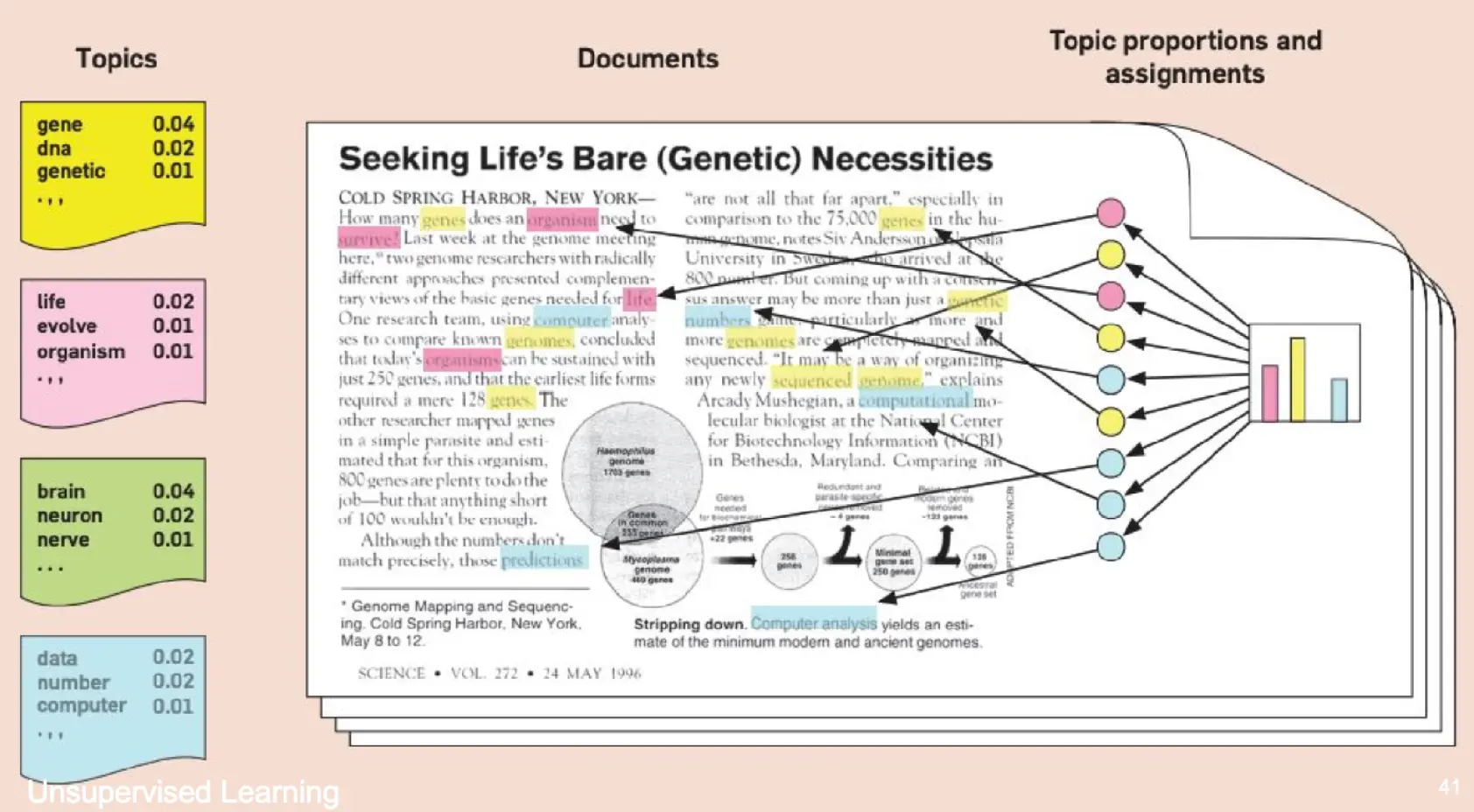LDA 假设文档是“先有主题，再有单词”生成的，目标是通过无监督学习找出隐藏的主题结构。 LDA本身是一个生成模型，其原理是，认为一篇文章遵守主题的分布，然后主题所对应的词也遵守分布，那么如果一篇文章由80%的主题A和20%的主题B组合而成，那么每个单词都是先采样主题，再在对应主题里面采样主题词所生成的。

但是，由于LDA这个过程是一个严格的采样过程，他就可以用贝叶斯推理给它逆过来，也就是说，你可以通过给定文章，来推断一个主题中对应主题词的概率，也可以推断一篇文章的主题分布。

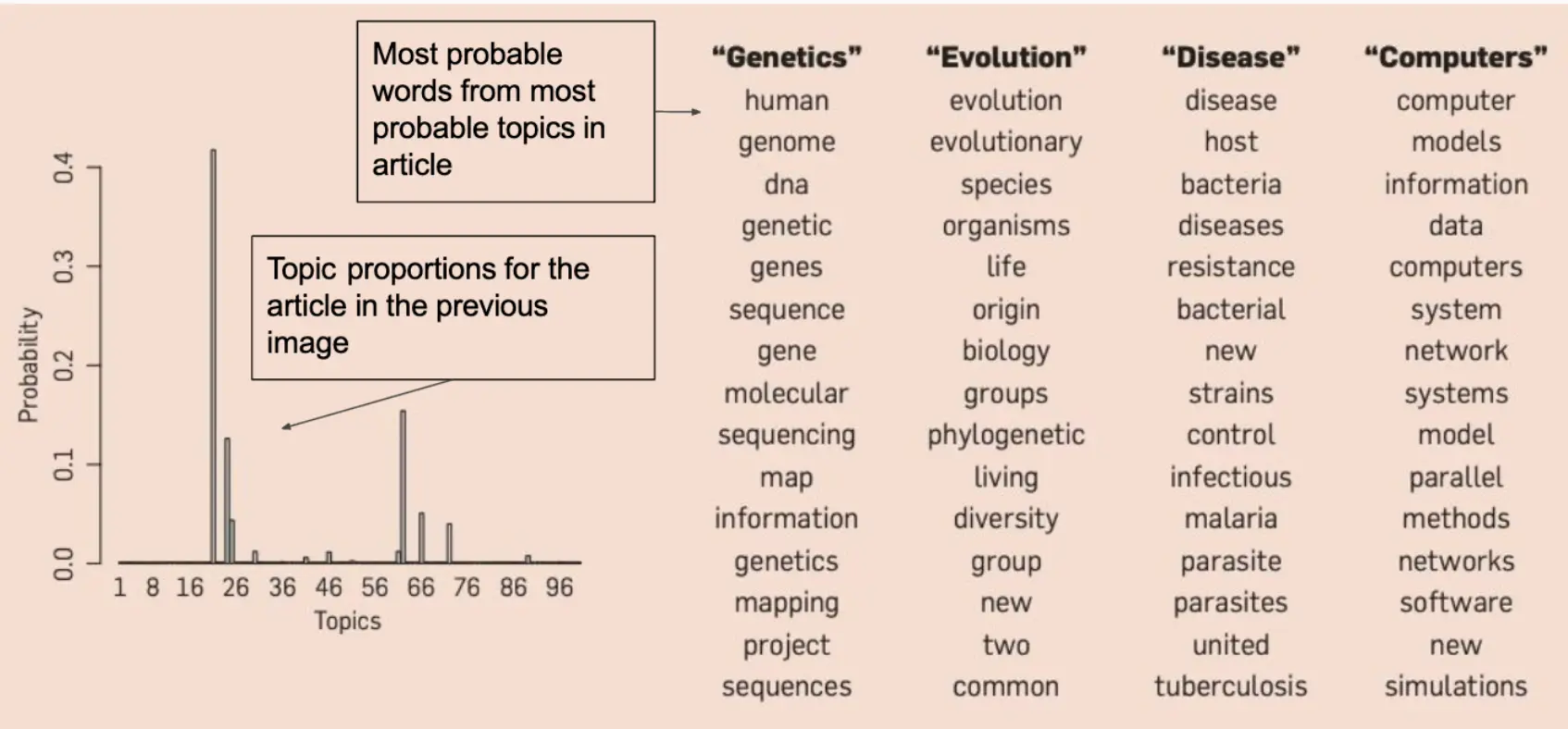例子： LDA经过训练之后，得到了3个主题的高频词分布： 主题 1: AI, deep learning, neural network, algorithm, data 主题 2: election, government, policy, law, president 主题 3: football, game, player, goal, team

LDA在经过训练之后，已经提前知道了一堆词和一堆主题的对应关系，也就是说LDA知道了P(单词|主题)，以及P(主题|文章)，然后LDA拿到一个文章后，对每个词，不断通过贝叶斯反推不断计算P(主题|单词)来为每个词分配到一个合适的主题

当我们拿到一篇文章，这里用一句话举例子： AI is transforming government policy and sports analytics.

那么流程就是；

1. LDA 先随机分配单词到主题（初始化）
   • "AI" 可能被分到 主题 1，"government" 可能被分到 主题 2，但这只是随机的。
   • 此时 主题 1、2、3 还没有名字，我们不知道它们代表什么。
2. LDA 通过贝叶斯推断（如吉布斯采样）反复更新主题分配
   • 通过计算 P(主题 | 文档) 和 P(单词 | 主题)，不断调整每个单词的主题归属。
3. 主题 1 可能含有 "AI, neural network, model, deep learning" → 其中AI的概率最高，那么这个主题就叫AI。主题 2 可能含有 "government, policy, election, law" → 其中goverment概率最高，那这个主题就叫goverment。

重新写一下LDA的训练以及推理过程

LDA模型假设一个模型是先选定主题分布 ${\theta }_d$ ，再针对每个词位置抽词。 其中，主题-词分布为：

$${\varphi }_{k,v}=P(w=v\mid z=k),$$

z为主题，k为主题编号，w为词，v为词编号。 文章-主题分布为：

$${\theta }_{d,k}=P(z=k\mid d),$$

d为给定文章。

训练

LDA训练只需要一堆文章语料，以及所期望的k的数量（主题数量），不需要其对应的主题，或者分布。 训练过程中，先随机把语料中的每个词分配一个主题标签z，然后对每个词做一些基于Gibbs 采样的迭代更新。反正训练结果是得到了： 主题–词分布，给定主题k，我就能知道其词v的分布：

$${\varphi }_{k,v}=\frac{n_{k,v}+\beta }{n_k+V\beta }.$$

以及文档–主题分布，给定文章d，我就能知道其主题的分布：

$${\theta }_{d,k}=\frac{n_{d,k}+\alpha }{N_d+K\alpha }.$$

推理

目标：给定一篇未见过的文档，计算它的 ${\theta }_d$ 首先我们把文章拆成语料，然后在文章上做Gibbs 采样，直到收敛。 接下来，我们就能得到：

$${\theta }_{d,k}=\frac{n_{d,k}+\alpha }{N_d+K\alpha }.$$

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update