Week 10 Reinforcement Learning

字数

1746 字

阅读时间

7 分钟

什么是强化学习

一种ML类型，Agent通过与环境做出交互，试探动作来获得奖励/惩罚。目标是学习一种策略，以最大化累计奖励。

在需要训练代理根据复杂、不确定或动态环境做出决策的情况下特别有用。

• 自动驾驶：复杂的交通情况，天气，道路障碍
• 股市：地缘政治，经济动荡
• 医疗诊断

在RL中，agent自动从没有标签的数据中学习，agent从自己的经验中学习。 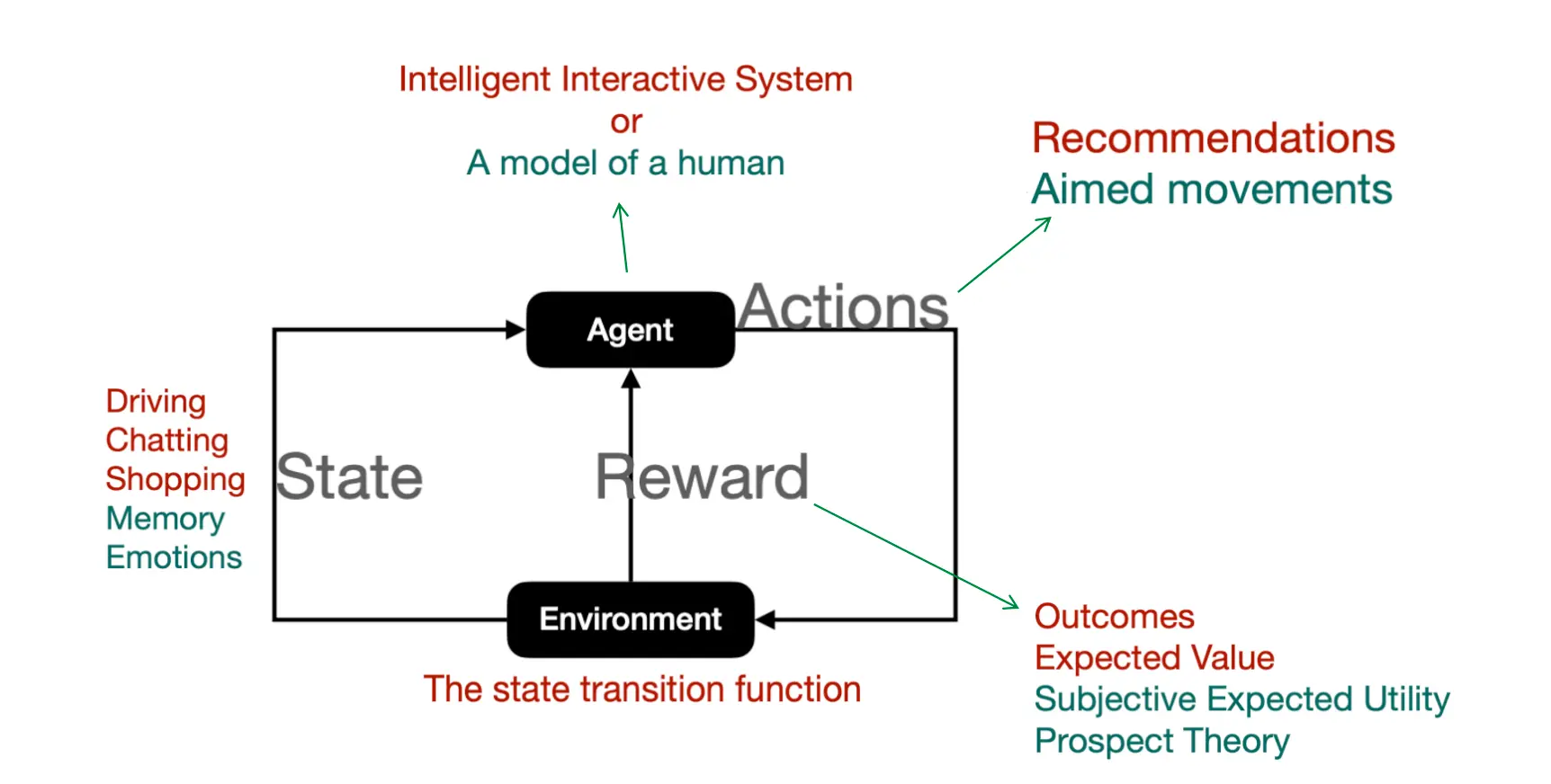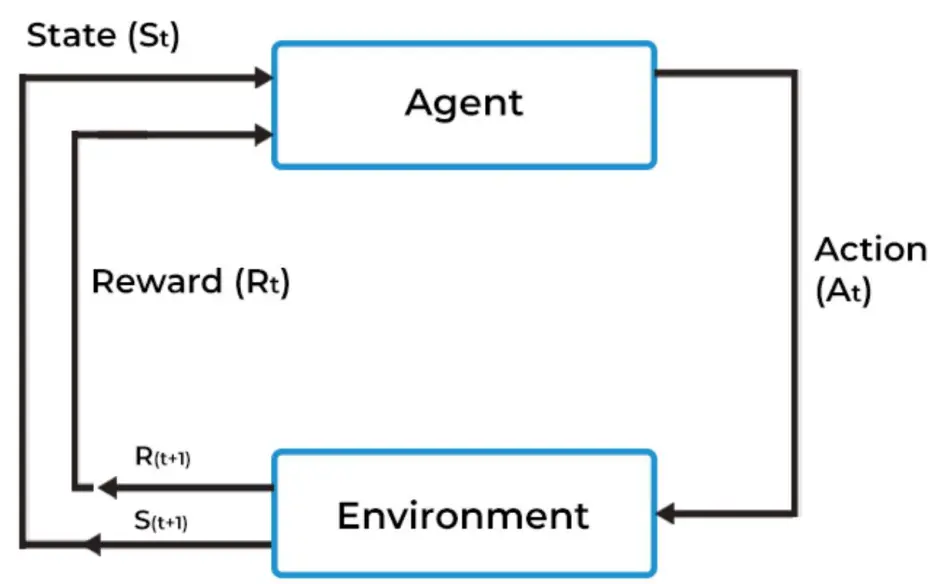Agent是ML algorithm，或者自动系统，环境是指有属性（例如变量、边界值、规则和有效操作）的适应性问题空间。 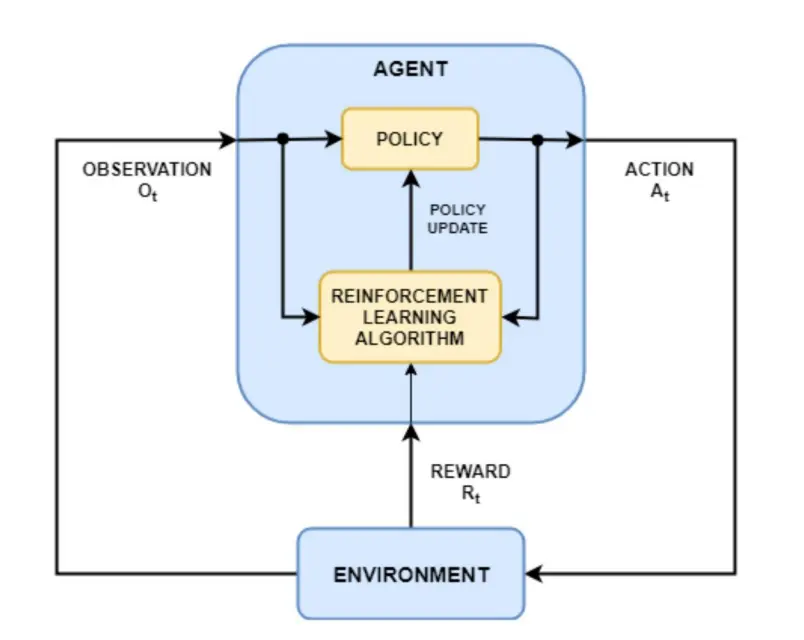一些问题用到了RL：

• Cart-Pole Problem
• 机器人运动
• Atari Games

MDP

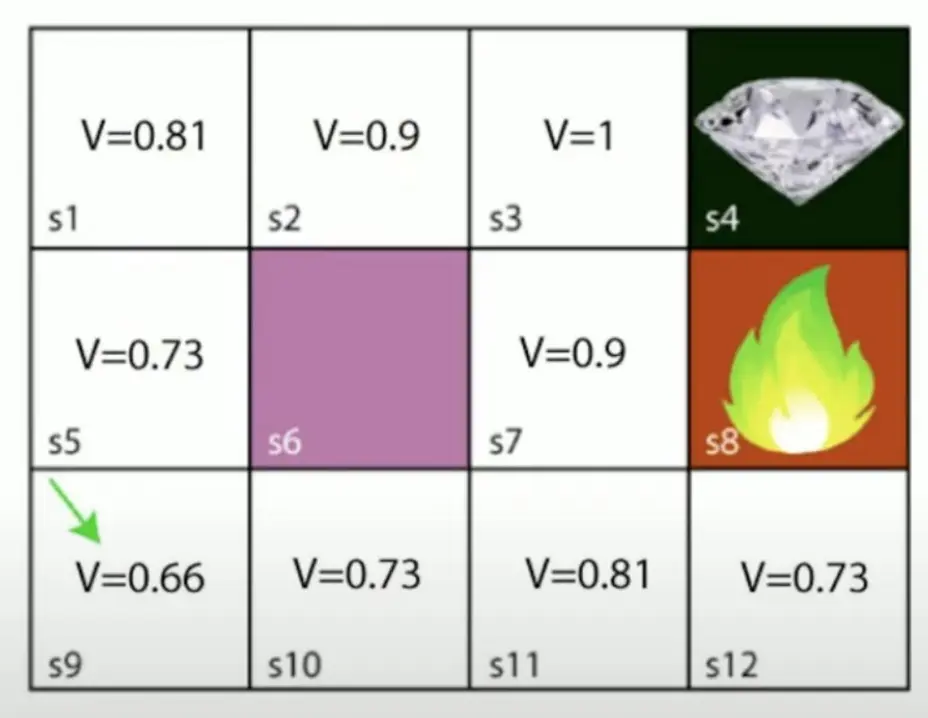
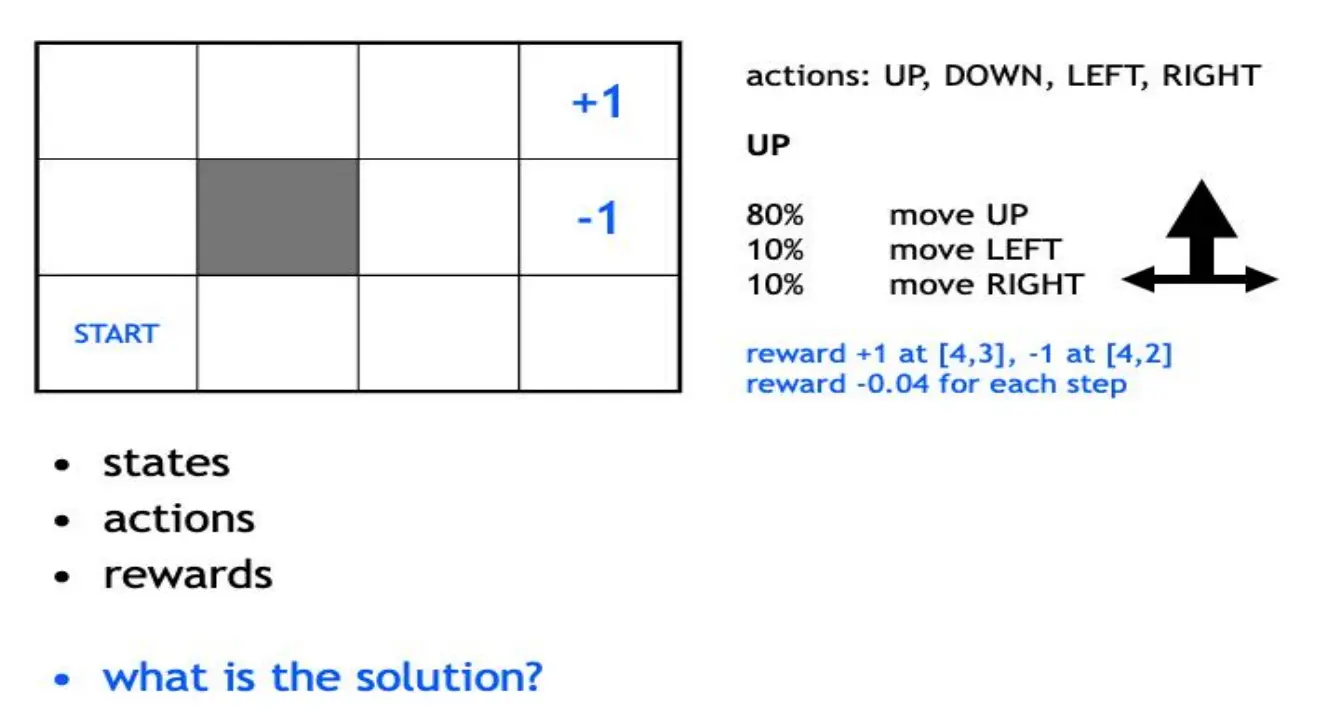注意，每一步奖励是-0.04

这是否是最优解呢？不一定。 因为agent在80%的概率是朝着正确方向走的，还有20%的概率偏离。因此，上图策略在实际执行中可能因为偏移导致撞墙、或者错过终点，未必能最大化期望回报

本例真正的“解”是要找出最优策略𝜋∗，在随机转移和折扣回报下最大化

当每一步reward为-0.1的时候，策略为： 当为-2时，策略为：（宁愿踩上-1，也要快速到达+1） 当为+0.01的时候，那就一直不到，远离最好： 如何形式化建模一个RL问题？用MDP。 一个策略 π 是指指定在每个状态下要采取的操作的函数。 我们的目标是找到最优策略 π*，能够最大化累计折扣reward：

$$\sum _{t\ge 0}{\gamma }^t{r}_t$$

我们真正要解的是，如何在所有可能的策略中，选出那个能够最大化未来奖励之和的策略 π*。由于初始状态、状态转移具有随机性（transition probabilities），我们不能只看单次轨迹，而要最大化期望累积奖励。 所以形式化定义为：

$${\pi }^{\ast }=\arg \underset{\pi }{max}\mathbb{E}[\sum _{t\ge 0}{\gamma }^t{r}_t|\pi ]$$

即在所有策略中，选择使期望折扣累积奖励达到最大者。 我们定义Episode（回合）为：

• 从智能体处于某个初始状态（initial state）开始，按照策略不断选择动作、观察新状态并获得奖励，直到 达到某个终止条件。

折扣机制

强化学习中，我们关心的是随时间累积的回报，不同的计量方式有两种常见形式：

• Additive rewards（累加回报）：
  • $$V(s_0,s_1,\dots )=r(s_0)+r(s_1)+r(s_2)+\dots$$
• Discounted rewards（折扣回报）：
  • $$V(s_0,s_1,\dots )=r(s_0)+\gamma r(s_1)+{\gamma }^{2}r(s_2)+\dots$$
  • 引入折扣因子，对未来的奖励打折扣。因子越小，越“偏好”即时奖励，因子越接近1，则更看重长期回报。
  • 折扣机制能保证在无限回合下收敛，也可以刻画风险偏好和任务时长偏好。

Value Function 状态价值函数

估计从给定状态s开始，按照某个策略执行时，智能体能获得的期望累积未来奖励。

$$V^{\pi }(s)=\mathbb{E}[\sum _{t\ge 0}{\gamma }^t{r}_t\mid s_0=s,\pi ]$$

Q-Function 状态-动作价值函数

比Value Function多了一个这一步要采用的动作。用于估计在给定状态 s 下，执行某个动作 a，然后按照策略 π 继续进行时，智能体所期望获得的累积未来奖励。

$$Q^{\pi }(s,a)=\mathbb{E}[\sum _{t\ge 0}{\gamma }^t{r}_t\mid s_0=s,a_0=a,\pi ]$$

明确考虑了在状态 s 下执行动作 a 的后果，因此能帮助智能体评估每个可能的动作。 状态价值函数可以看作是状态-动作价值函数 Q 对所有可能动作的期望。

$$V^{\pi }(s)={\mathbb{E}}_{a\sim \pi (\cdot |s)}[Q^{\pi }(s,a)]$$

Bellman Equation 贝尔曼方程

贝尔曼方程描述了如何递归地计算一个状态的价值V(s)。

$$V(s)=\underset{a}{max}[R(s,a)+\gamma V(s^{\prime })]$$

例子：

Q-Learning

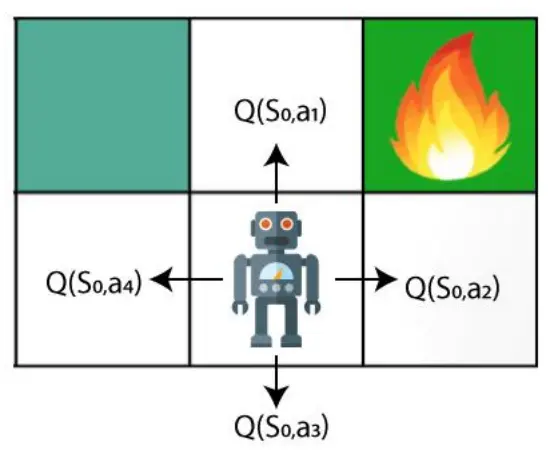对于这个例子，代理将根据概率基础采取行动并进行更改。我们需要在Q值方面进行一些更改。

Q-learning是一种 无模型：这意味着它不需要知道环境的动态或转移概率。换句话说，Q-learning 不依赖于环境的具体转移模型（即状态如何根据动作转移，及这些转移的概率）。 基于价值：关注的是学习 状态-动作价值函数 Q(s,a)， 离策略算法，更新 Q 值时，可以使用不同于当前策略的数据，通常使用的是探索策略（如 epsilon-greedy 策略）。 将根据代理的当前状态找到最佳的一系列动作。 “Q”代表质量。质量表示动作在最大化未来奖励方面的价值。

Q-table 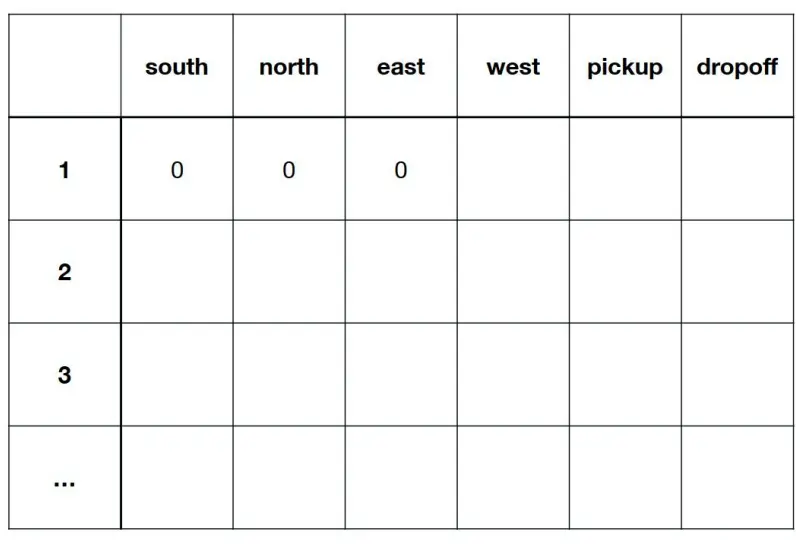Q-learning Open: Pasted image 20250429141831.png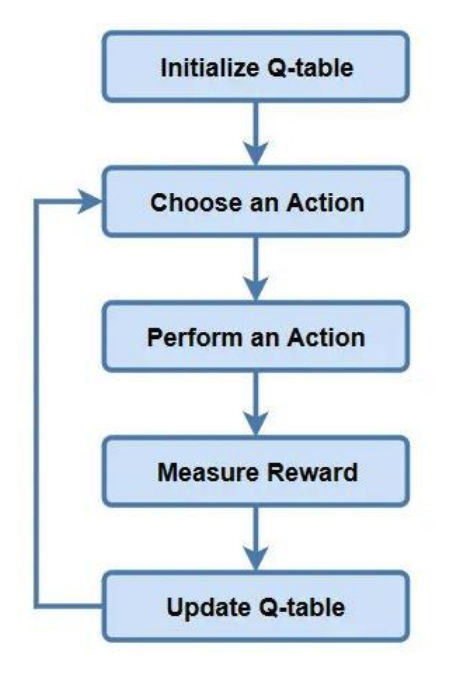

• 初始化 Q 表：对于每个状态s和动作a，初始化 Q 值Q(s,a)为0
• 观察当前状态s
• 选择一个动作：在当前状态s下，智能体选择一个动作a并执行，选择的方式通常是 探索或 利用，例如通过 epsilon-greedy 策略选择。
• 接收即时奖励r，执行动作后，智能体会从环境中得到即时奖励r，这个奖励可以是正值或负值，表示该动作在当前状态下的效果。
• 观察新的状态s',
• 更新 Q 值：通过贝尔曼方程来更新 Q 表
  • $$Q(s,a)=r(s,a)+\gamma \underset{a}{max}Q(s^{\prime },a)$$
• 更新状态s <- s'

例子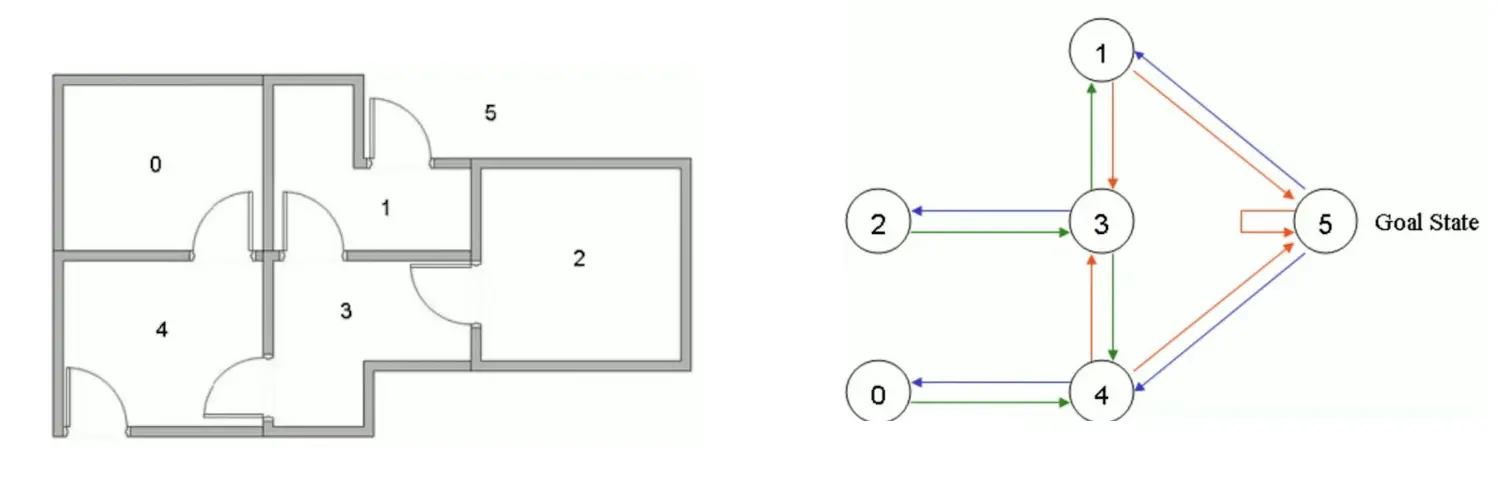： 我们定义一下Reward：

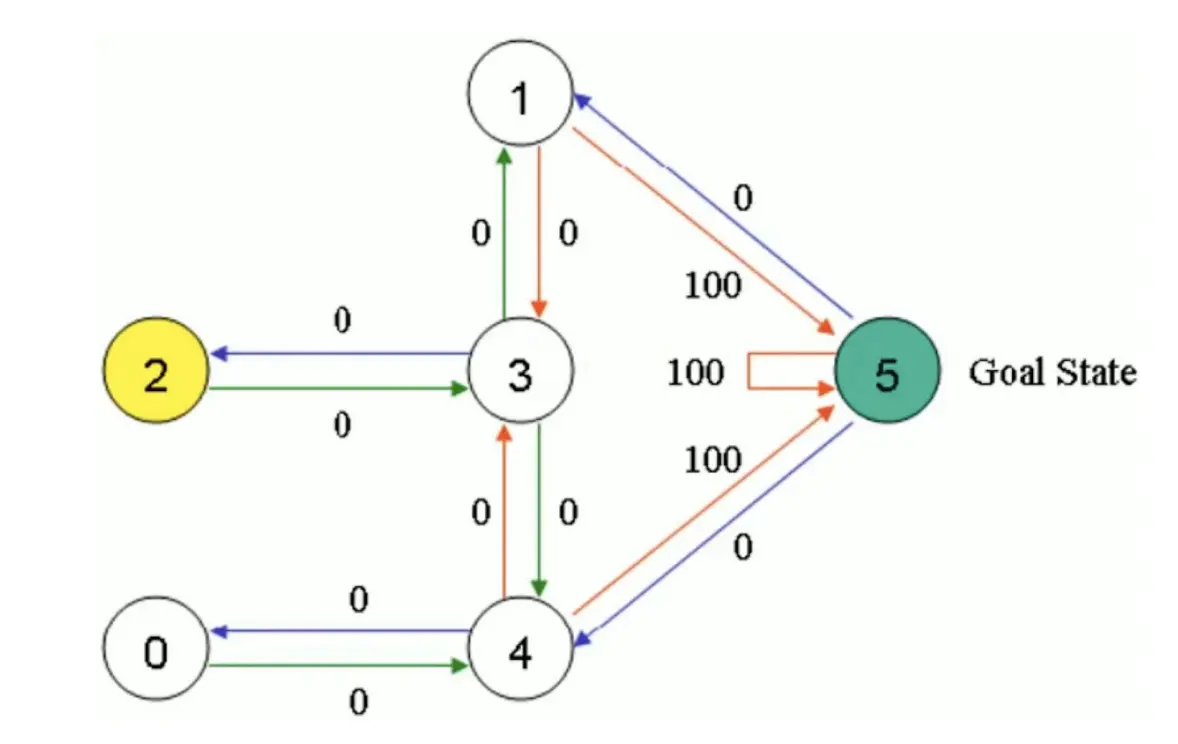首先，初始化Action表和Q表： 我们把状态1当做起始状态。要么去3，要么去5，显然去5，所以选择去5。那么我们想要更新Q表。5能到1,5,4 Q(1,5) = Reward(1,5) + 0.8max[Q(5,1), Q(5,5), Q(5,4)] = 100 + 0.8 *0 = 100 所以更新： 然后我们还是随机取一个起点，比如说3，能去1,2,4。比如说要去1. 那么Q(3,1) = R(3,1) + 0.8max[Q(1,3), Q(1,5)] = 0 + 0.8 * 100 = 80 更新Q表： 最后不断迭代，得到：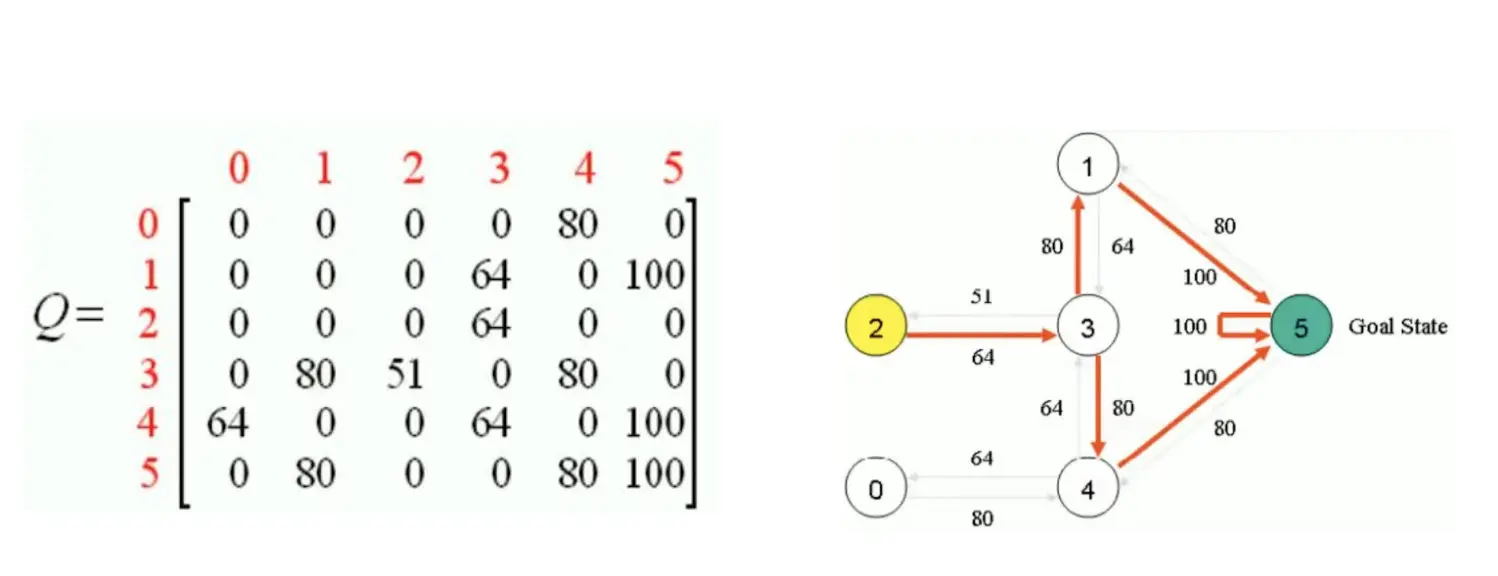

每次更新完 Q 表后，智能体的起点和动作选择可以是随机的。但是否完全随机依赖于所使用的探索策略。Q-learning 是一种 离策略（off-policy） 学习算法，因此它允许使用不同的策略来生成数据，并且不需要当前的策略来做出动作选择。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update