Logistic Regression
Hypothesis Set
首先回顾一下监督学习的定义:
在给定训练集T的情况下,学习一个mapping,由输入X映射到输出y。\
%20(1)%20(1)%20(1)%20(1).D_-kgMZh.png)
那么下图就说明了一个有监督学习的所有组件:
%20(1)%20(1)%20(1)%20(1).kfCU7sHV.png)
别的都好说,这个Hypothesis Set是什么呢?其实就是所选定的函数型,比如线形之类的。为什么有这玩意呢?因为传统的机器学习方法基本都是给定一个函数型,然后去学习里面每个w的大小,组合出一个完整的映射,来看性能。如果类比到深度学习里面,其实hypothesis set就是网络,比如说CNN,Transformer,RNN之类的,你先挑一个网络,然后进行梯度下降,最后比较精度。
有监督学习解决什么问题呢?
给定一个训练集,训练集怎么来的呢?从所有样本中,以一种未知但固定的概率从中独立同分布地抽出来的。目标是学习一个可泛化在未看见过的样本上的映射。
%20(1)%20(1)%20(1)%20(1).BhwWTNLg.png)
逻辑回归
尽管名字是回归,逻辑回归用来处理分类问题。
在逻辑回归模型中,我们把一个样本x,以及其属于某个类别的概率(实际上是logit)表示为一个线性组合。
从深度学习的角度看,逻辑回归就是一个以sigmoid函数为激活函数的单层线形神经网络,输出的内容为0-1的一个概率。
在下面,我们聚焦在2分类问题。
那么sigmoid是怎么来的呢?就是从logit里来的。怎么来的?
我们想要用线形模型WX建模概率p,那么就有一个问题,WX的范围是-∞,+∞,我们想要建模一个函数h,使得wx的范围和h(p)范围一样,也就是wx = h(p), h-1(wx) = p
h是什么呢?h就是ln(p/1-p), 这玩意范围在-无穷,+无穷,对上了,就能用。
而我们就把h,也就是logit的反函数就叫做sigmoid,1/(1+e-wx)
那么我们总结一下逻辑回归到现在的内容。wx越大,离的决策边界越远,置信度越高。正越大,p1越大,越负越p2.
怎么学W?Loss和极大似然
逻辑回归:极大似然法。
思想:我们进行一次采样,得出一个结果。我们认为,由于我们一次采样就采样到了这个结果,所以我们认为代表这个结果的概率密度就应当是最大的,所以我们求导=0就可以得到限制条件,从而得到想要的参数。
二项分布又称Bernoulli distribution
似然函数如下:
在一般情况下
- 如果X是离散的,那么就是所有情况f(x)的乘积
- 如果X是连续的,那么就是求f(x;θ)对x的边缘
根据极大似然的思想,可以得到估计结果:
这个函数怎么求最大值?先对齐log再求导,因为不改变其单调性。求导后这个玩意叫cost function
我们一般用负ln形式求导。一方面可以快速把乘转化为+,另一方面可以迎合loss function的形式,使loss最小即可。
这玩意如果进行一下数学推导,其实就是交叉熵loss, Cross Entropy Loss.
%20(1)%20(1)%20(1)%20(1).CZsmiVcq.png)
怎么推导的呢?首先y为概率,且为二分分布,所以输出只有两种,y和1-y
Py =P(y|x,w) = yP(1|x,w) + (1-y) (1-P(1|x,w)这就好理解了。
梯度下降
梯度下降通过迭代地调整w,沿着导致E(w)最大减少(最陡降)的方向。
.O_fBNGx3.png)
在逻辑回归上怎么弄呢?让交叉熵对w求导。图里面p(1|x,w)其实就是sigmoid(wx+b)。
这个梯度是怎么求的呢?其实麻烦就麻烦在这个p(1|x,w)怎么求导。其实很简单
因为p(1|x,w) = sigmoid(wx+b),而sigmoid(x)的梯度就是sigmoid(x)(1-sigmoid(x)),所以就好求了。
.LKQFw4sJ.png)
至于learning rate,太大会导致跳跃,太小会导致收敛太慢。
梯度下降是一个通用问题,但有可能卡在local minima。但是对于交叉熵不存在这个问题,因为交叉熵对于w严格凸,只有一个最小值。
那么梯度下降有什么问题呢?
• 梯度下降可能会陷入局部最小值。
• 但在使用交叉熵损失的逻辑回归情况下,这不是问题,因为被优化的函数是严格凸的。
• 我们还讨论了学习率过大可能会使找到最优解变得困难。
• 算法可能会跳过最优解。
• 学习率过小也不理想。
• 可能需要很长时间才能找到最优解。
牛顿-拉夫逊法 Newton-Raphson Method
假设一个损失函数是E(w) = w1^2 + w2^2,那么其三维图像为:
.CKpBMrS1.png)
从顶部向下看,等高线图为一个一个圈,这样梯度下降可以沿着最优方向找到loss最低点。那么如果E(w) = w1^2 + 4w2^2的话,就可以看到,不是指向椭圆中心的,而是不断跳跃的,这不是最优路径。
.dwLMpt2Y.png)
为什么会出现这样的现象?因为4是w2的参数,对w2求导的时候,w2的修正程度会大于w1。
标准化(减去平均再除以标准差)能解决这个问题吗?略微可以,因为你让输入变得稳定了,不偏向于某一边了,但是没有办法从根本解决4带来的差距。
带来这个问题的根源在哪里?在这里:
.DCTmwzj8.png)
我们可以看到,如果用传统的梯度下降,大梯度就有可能走大了,小梯度就可能走不动。那么什么东西能够看到梯度的大小呢?那就是梯度的梯度,也就是二阶导。二阶导数告诉我们曲率是多少(凸 +,凹 -)。我们可以利用二阶导数来判断梯度是否变化过大,并相应地进行较小的权重更新!NR方法就利用了这一点
Newton-Raphson更新法则:
.Bz5nhRlI.png)
这方法其实特别好推导。推导思路如下:
我们的目标不是梯度下降,我们的目标其实是寻找E(w)的最低点。理论上这个最低点是能通过求导算出来的,但是实际太麻烦了,那么怎么能够简化的同时逼近E(w)呢?就用泰勒展开逼近后,再找最低点。
我们知道,泰勒展开可以用多项式去逼近一个函数,展开越多越像。那么我们应该展开多少层呢?在这里选择了2层,因为我们知道,二次方程很容易求解,三次以上就不好求了。根据泰勒展开的公式,我们可以把任何一个E(w)进行degree为2的泰勒展开:
.DRAFUId2.png)
接下来,我们想要找到这个函数的最低点,怎么办?求导为0,很自然就得到了更新公式:
.b6xj-wnX.png)
多变量下的牛顿拉弗逊法
首先我们定义Hessian矩阵,这玩意没啥意义,就是为了涵盖所有我们需要的导数,好引用,从而形式优美:
.Bb-qJNN3.png)
那么,我们就可以得到多变量情况下的迭代公式:
.CBH_vOob.png)
用了都说好!
.Dc2dcauc.png)
- 这样的更新将在一步中将我们带到二次逼近的最优点。
- 然而,由于二次逼近与真实函数差距较大,并非真实损失函数,我们需要迭代应用这个规则。
- Hessian矩阵的计算代价特别大,在深度学习里面基本算不出
- Newton-Raphson 法的主要应用场景是凸优化问题,而深度学习中的损失函数往往是非凸的,尤其是深层神经网络。这种情况下,Hessian 矩阵可能是非正定的,Newton-Raphson 法可能会因为负的二阶导数导致更新方向错误。
非线性变化
.C1ffGJMb.png)
.DU6bFriZ.png)
显然,这两种情况下,用一条线(上),或者一个点(下)都是分不开两种类型的,这个时候就需要非线性变化了。
.DpGAWsWx.png)
那么,什么样的高维embedding能使得我们在高维度使得问题变得线形可分?
遵循以下规则:
degree限制好之后,就是排列组合所有低于degree的变量组合
(1, x1, x2) = 1, x1, x2, x1^2, x2^2, x1 x2, x1^3, x2^3, x1x2^2, x1^2 x2
.BZyBUMFi.png)
例子:
.DrZHBqMP.png)
.BxbqCful.png)
通过非线性变化的方法,得到的决策边界其实对于原空间没啥用,重要的是得到真正的w, 从而可以在原空间中计算出边界。特征空间中的线性决策边界仅仅是一个中间结果,我们关心的是得到 w 的值。那个直线的线形边界只是比较好看而已罢了。
也可以使用其他别的embedding
.O_XOP9v-.png)
大多数时候,我们把问题映射到一个高维空间,但也不必要。如果我们不需要其中的一些东西,也可以省去:
.R_IUsLNy.png)
然而实践中,我们通常事先不知道需要哪些嵌入,因此我们经常会将问题转化为更高维度的嵌入。
非线性变化在逻辑回归中
.DS-kE4FF.png)
- 选择一个非线性转换。
- 将其应用于训练示例,使其具有格式(Ф(x), y)。
- 基于转换后的训练示例创建一个线性模型(使用我们迄今学到的相同学习算法)。
- 通过用取决于X的相应值替换;Ф(x) 来确定(非线性)模型。
.Dju2mbs_.png)
优点:
线性模型通常与相对高效的学习算法相关联。
它们可以是稳健的,并具有良好的泛化性能。
注意事项:
维度的数量可能变得非常高。
选择一个非线性转换,使训练示例很好地拟合,并不一定意味着会有良好的泛化。这可能导致过拟合。
.CWhJ6-BS.png)
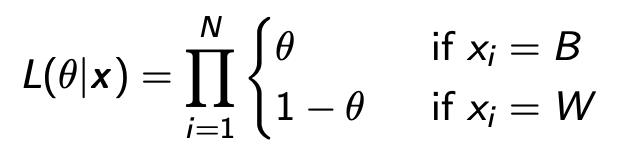
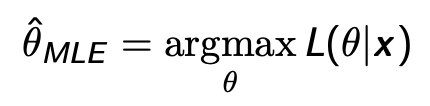
 Larry Shi
Larry Shi