Larry's Knowledge Base

字数

1411 字

阅读时间

6 分钟

 # Runtime Analyse

Intro

对于一般CS的算法来说，我们关注两个点：

正确性
计算复杂度，也就是时间复杂度对于进化算法或者启发式算法来说，我们关注的点就更偏向于：
敛散性，是否能在有限时间内找到解？
时间复杂度，常通过“适应度函数调用次数（fitness function evaluations）”来度量

Convergence (敛散性)

理想情况下，进化算法（EA）应该在有限步内以概率 1 找到最优解。如果算法找到最优解后能一直保留这个解，那么就说算法收敛（converges）到最优解。

要让一个EA在数学上保证收敛到最优解，必须满足以下两个条件：

从任何一点出发，有正概率能够到达搜索空间中任意一点。
找到的最优解永远不会从种群中被移除

所以，一般的GA不保证收敛，带精英策略的进化算法会收敛。

在现实中，大多数 EA 确实最终能找到最优解。但更关键的问题是到底需要多久才能找到最优。

Computational Complexity of EAs

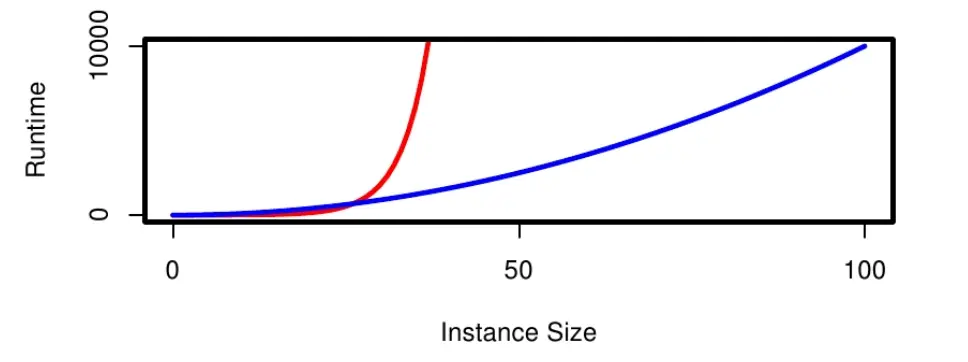红线：指数级复杂度（Exponential runtime），蓝线：多项式级复杂度（Polynomial runtime）。在EA中，适应度函数的评估成本远高于其他操作，而不是交叉、变异等操作。所以 EA 的复杂度分析通常用“评估次数”来表示，而不是简单的操作数。进化算法是随机算法，即使输入相同，每次运行的操作也可能不同（因为随机选择、突变等）；即使初始种群一样，每次运行的最终输出结果也可能不同。

因此，EA 的运行时间本质上是一个随机变量，记作 $T_{f}$ 表示在目标函数f下，算法完成任务所需的评估次数。

对于这个随机变量，我们关心两个东西：

期望运行时间 $E (T_{f})$ ，表示平均下来，EA 要用多少步（评估次数）找到最优解。
成功概率 $P (T_{f} <= t)$ ，表示 EA 在不超过t步内找到解的概率。

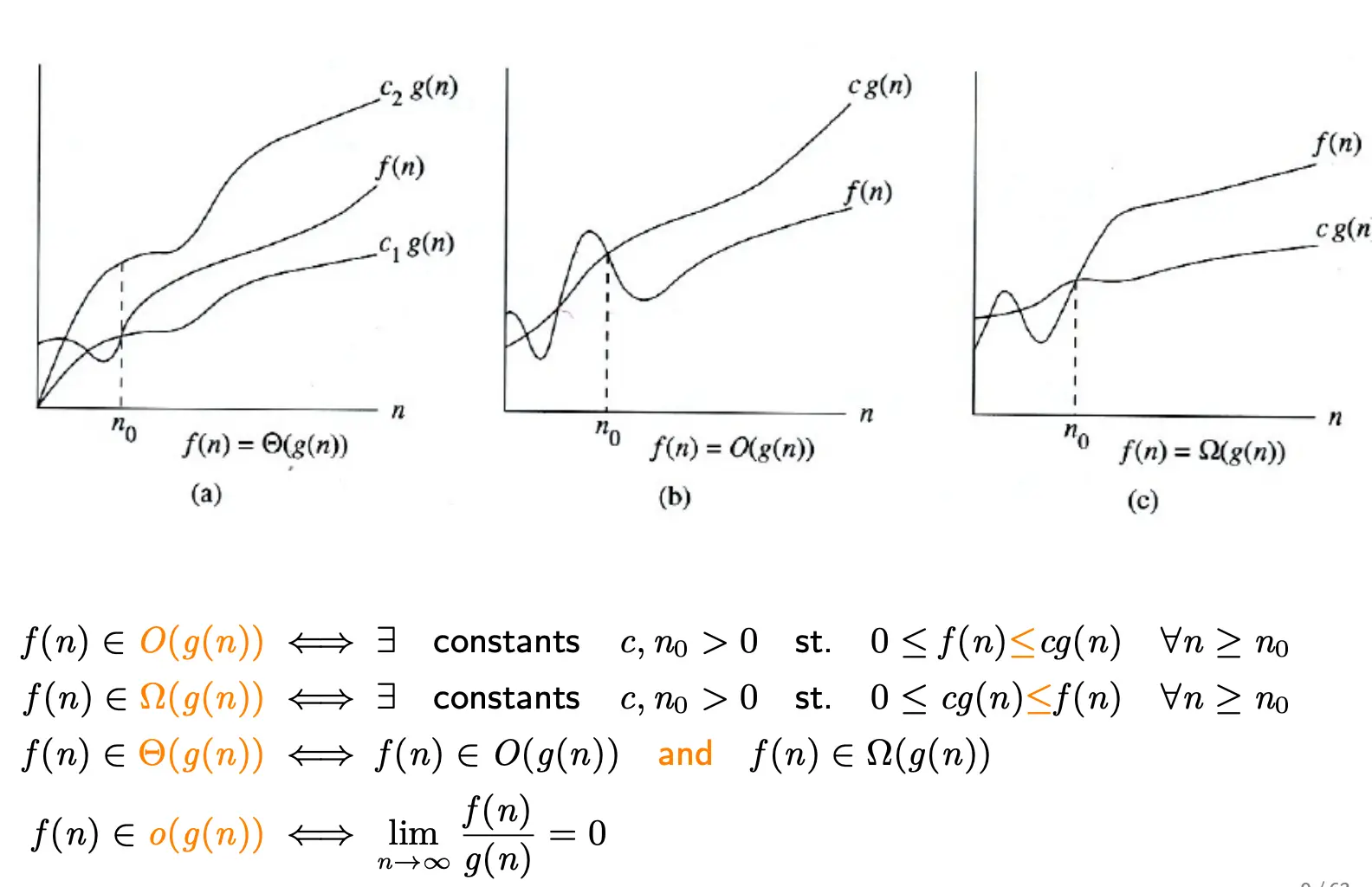
Asymptotic notation 渐进标记

(μ + λ) EA 分析

μ 表示种群大小 λ 表示每一代中新生成的“子代”个体数。

如果μ λ都是1，那就是1+1 EA 也就是没次突变之后，如果突变得到的结果优于目前的这一个结果，那么就替换，如果不优于，那就不替换。更特殊地，如果突变没次只突变一位的话，那其实就是Random Local Search (RLS)

那么我们接下来针对1+1 EA进行一个分析。首先，根据经验，我们把突变率设置位1/n。那么突变位数的期望就是：

E (X) = n \times (p \times 1 + 0 \times (1 - 1 / n)) = n p = n \times 1 / n = 1

那么我们计算一下，一串n里面，只有1位flip的概率。

P (X = 1) = C_{n}^{1} \cdot p \cdot (1 - p)^{n - 1} = (1 - 1 / n)^{n - 1} >= 1 / e \approx 0.37

而2位flip和0位flip的概率分别是

P (X = 2) \approx 1 / 2 e, P (X = 0) \approx 1 / e

ONEMAX分析

ONEMAX函数：输入一个二进制串，输出1的个数。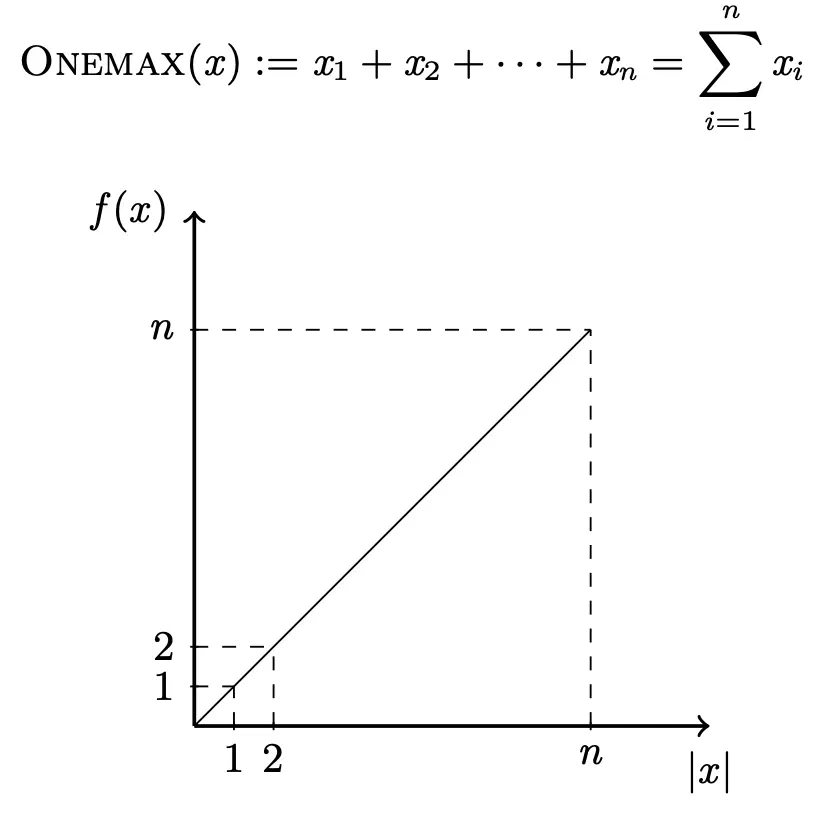

在分析ONEMAX之前，我们先来引入一个概念，Fitness-based Partitions，按适应度分区。

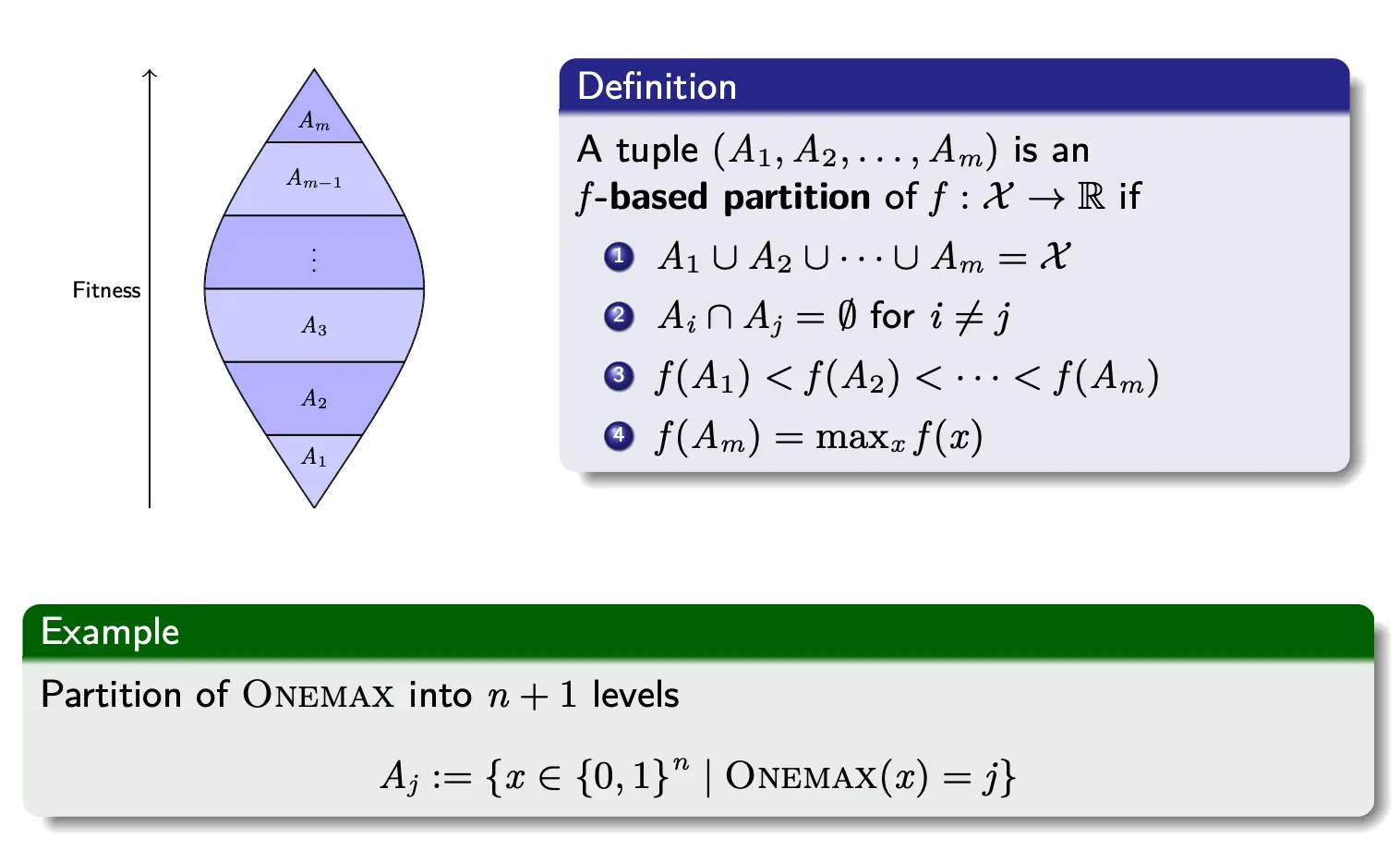按照fitness分区。要满足上面的4点定义。例子，A3就是ONEMAX(x) = 3的个体集合。

接下来我们要尝试证明，1+1 EA在ONEMAX问题上的时间复杂度是O(nlnn) 首先定义一系列符号。 j是任意一个大于i的数。我们可以知道，ui为Ai往上走的概率，那么脱离Ai的期望尝试次数就是E(Ti) = 1 / ui。这是几何分布的期望公式。那么我们现在想要知道整个运行时间T，那么其实就可以转化为：

E [T] \leq \sum_{i = 1}^{m - 1} s_{i} E [\sum_{j = i}^{m - 1} T_{j}]

这公式其实很好理解，外层求和是分配算法初始在第Ai层的权重。而注意这里是小于等于，所以是上界，内层循环是处于Ai往上能跳的期望步数。我更愿意写成这样：

E [T] \leq \sum_{i = 1}^{m - 1} s_{i} \sum_{j = i}^{m - 1} E (T_{j})

这个上界的冗余来自于用 $\sum_{j = i}^{m - 1} E (T_{j})$ 来替代准确的从Ai跳到Am的期望步数。那么继续推导

\sum_{i = 1}^{m - 1} s_{i} \sum_{j = i}^{m - 1} E (T_{j}) = \sum_{i = 1}^{m - 1} s_{i} \sum_{j = i}^{m - 1} 1 / u_{j} \leq \sum_{j = i}^{m - 1} 1 / u_{j}

有了这个结论之后，我们继续推导。 Aj表示有j个1，n-j个0 那么uj也就是从Aj跳到任意更高层，最简单的方式是反转一个0到1，其他位不变。那么就有：

u_{j} \geq (n - j) \cdot 1 / n \cdot (1 - 1 / n)^{n - 1}

1/n为选中一位变异的变异概率，n-j是0的数量，第三部分是其他位不变。而

(1 - 1 / n)^{n - 1} \geq 1 / e

所以我们有一个下界

u_{j} \geq \frac{n - j}{e n}

把这个东西带入回去。

E [T] \leq \sum_{j = i}^{n - 1} 1 / u_{j} \leq \sum_{j = i}^{n - 1} \frac{e n}{n - j} = e n \sum_{i = 1}^{n} \frac{1}{i}

这里最后一步是把j=0到n-1换成了i=1到n 而根据调和级数：

\sum_{i = 1}^{n} \frac{1}{i} = \ln n + γ \approx \ln n

所以$$\mathbb{E}[T]\leq en\cdot(\ln n+1)=\mathcal{O}(n\ln n)$$

贡献者

Larry Shi

文件历史

最后编辑于 3 天前查看完整历史

Intro ​

Convergence (敛散性) ​

Computational Complexity of EAs ​

Asymptotic notation 渐进标记 ​

(μ + λ) EA 分析 ​

ONEMAX分析 ​

贡献者 ​

文件历史 ​