Week 6 EDA and Genetic Programming
EDA 是什么
EDA （Estimation of Distribution Algorithms）是通过避免使用如交叉互换和突变这种变化算子，通过某种方法挖掘已有种群中优秀个体的分布，并在这个分布中采样新个体来达到相同目的的一种算法。
基本流程： 
如果图示的话就是这样的： 
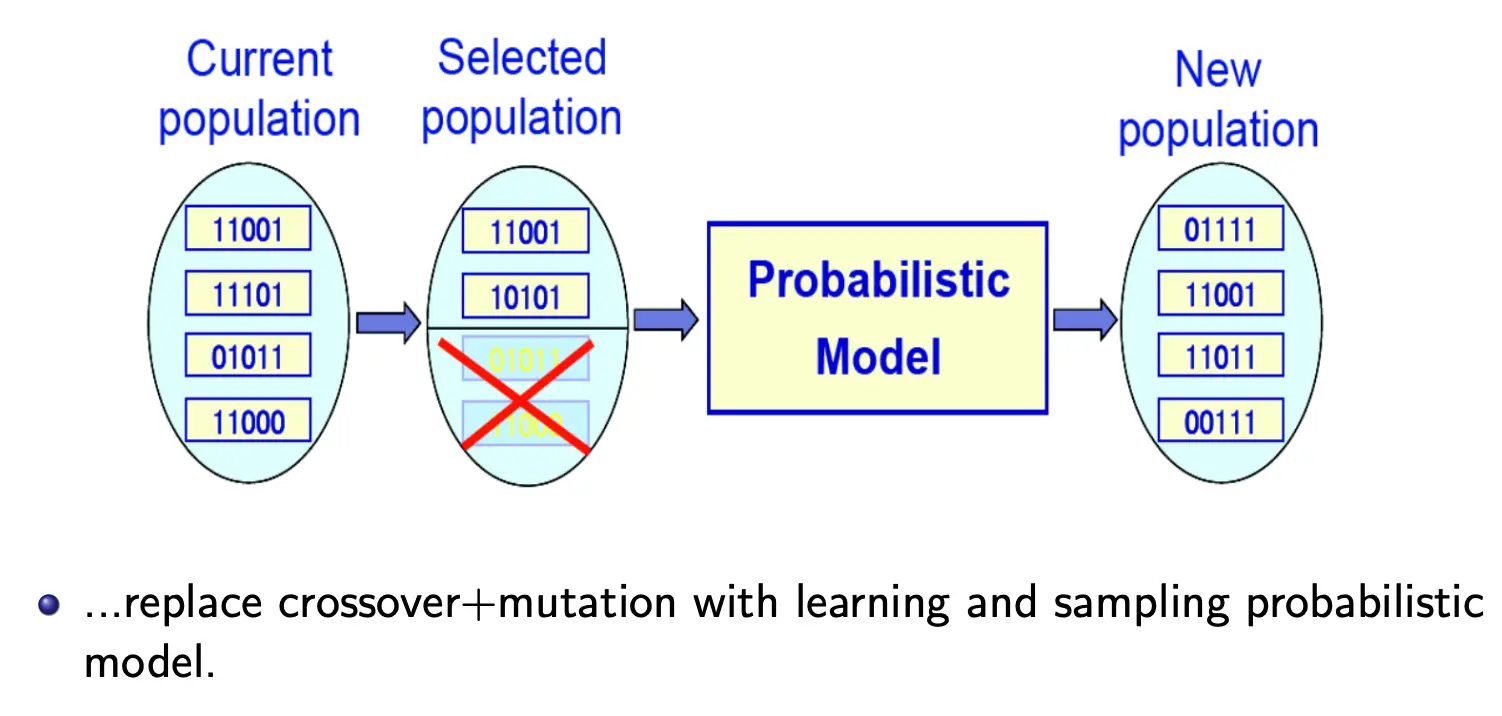
Univariate Marginal Distribution Algorithm (UMDA)
单变量边缘分布算法。想法特别简单，就是通过在已有优质种群中统计1和0的频率来去估计其概率分布。
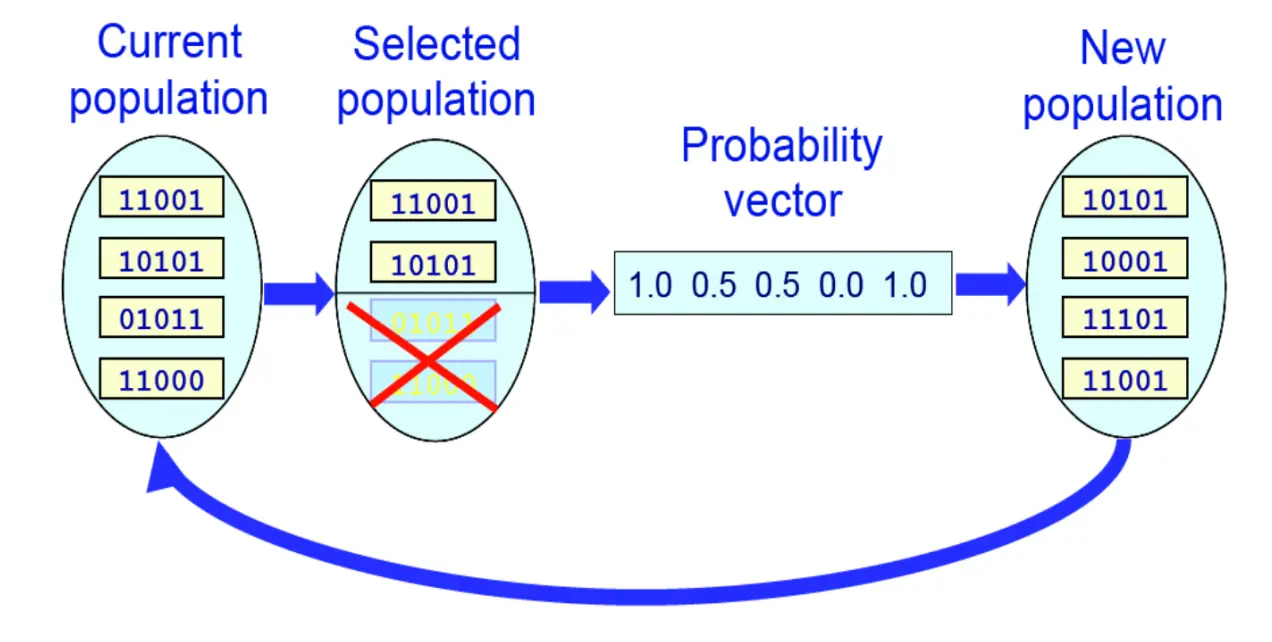因为基因型的每一位都是独立的，所以整个一整个基因串的概率分布就是每一位概率分布的乘积。 
如果把这个过程用伪算法语言描述，那么就是这样的： 
即为，p0的时候，所有位取1的概率都是1/2 然后进入循环，通过p0_i来采样，计算fitness，保留下一代，再重新计算新一代的p1_i。计算方法是算1的频率。
然而，如果凑巧某一代的时候，种群中某一位上的所有个体都是1或都是0，那么它将永远无法从这个固定的数中逃脱，所以这时候需要给微小的概率让其逃脱： 
其他类型的EDA
EDA有不同复杂度的模型，从独立到成对再到多元依赖。不仅适用于离散搜索空间，也可以扩展到连续优化问题。
假设每个基因位都是独立变量的EDA
- UMDA已经介绍过
- Population Based Incremental Learning (PBIL) 本质上和UMDA类似，但加入了“记忆+遗忘”，每次更新概率向量时带一点历史遗传信息。
- Compact Genetic Algorithm (CGA) 极简GA，它的种群规模压缩到只用一个概率向量来记录当前最优解的统计特征，非常节省内存。
假设每个基因位都成对依赖彼此的EDA
- 考虑成对变量之间的依赖关系，比如bit i 和 bit j 之间的联合分布。这比独立型EDA更复杂，但能表达更强的模式。
多元依赖型
复杂但表达能力最强。常用一些图模型（如贝叶斯网络）来捕捉复杂结构。
Continuous EDA
EDA不仅能处理二进制问题，还可以处理连续变量优化问题。
- 计算个体的每个变量的均值和方差
- 用高斯分布来描述这些变量的分布。下一代个体从这个高斯分布中采样生成。
UMDA失败的例子：Concatenated traps
虚晃fitness function 
在5个bit都是1的时候获得最高fitness，否则，1越多fitness越差。
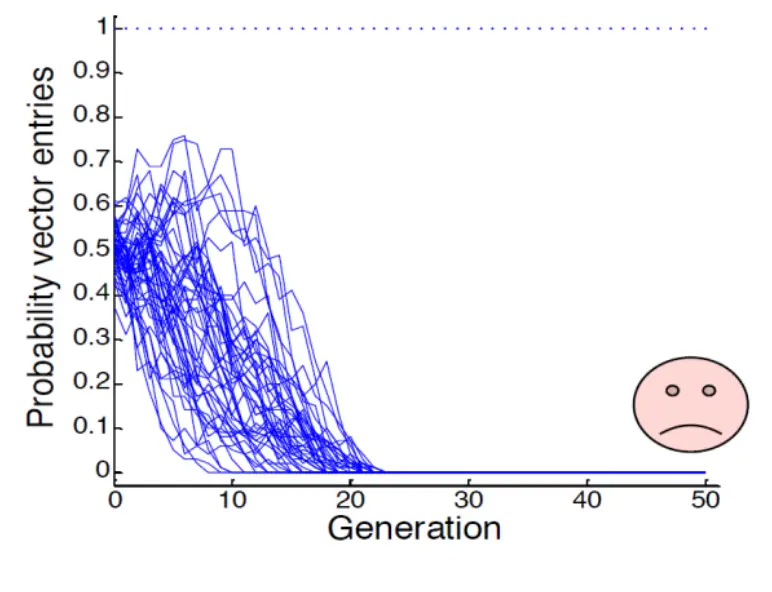失败的原因是局部最优和全局最优有很大的gap。Trap问题的最优解是一个整体模式，光靠独立bit的统计是不够的。 所以对于有结构，需要看整体的问题时，我们需要整体考虑。
如果我们统计的是5-bit整体模式，比如"00000"、"11111"，而不是"每个位的0/1概率"，那么：
- "11111"（全局最优）会比"00000"（局部最优）更明显地表现出来。
- 统计的是模式整体的概率，而不是bit的独立概率，这样就不会被单bit误导。
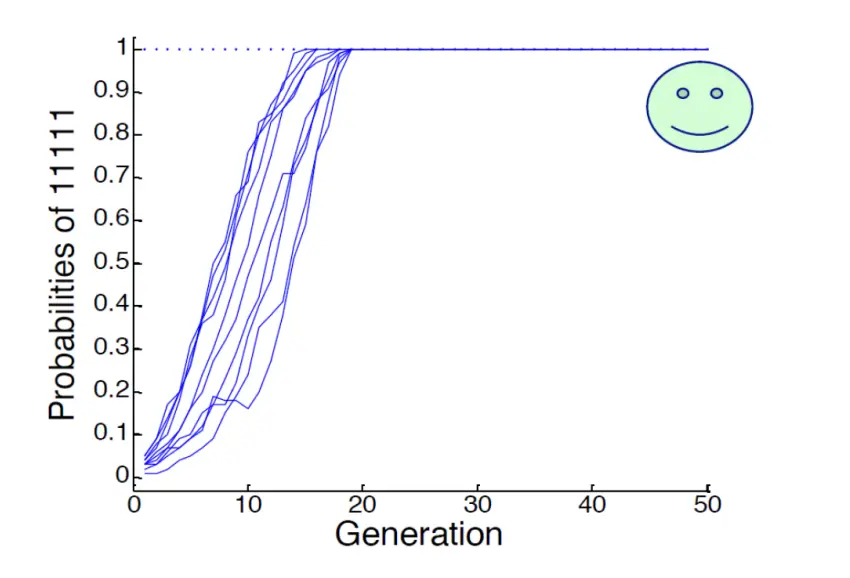但是这种成功是在我们已知了问题的结构（即要考虑5位）的情况下得到的。在实践中，我们如何做呢？
我们用BOA，Bayesian optimisation algorithm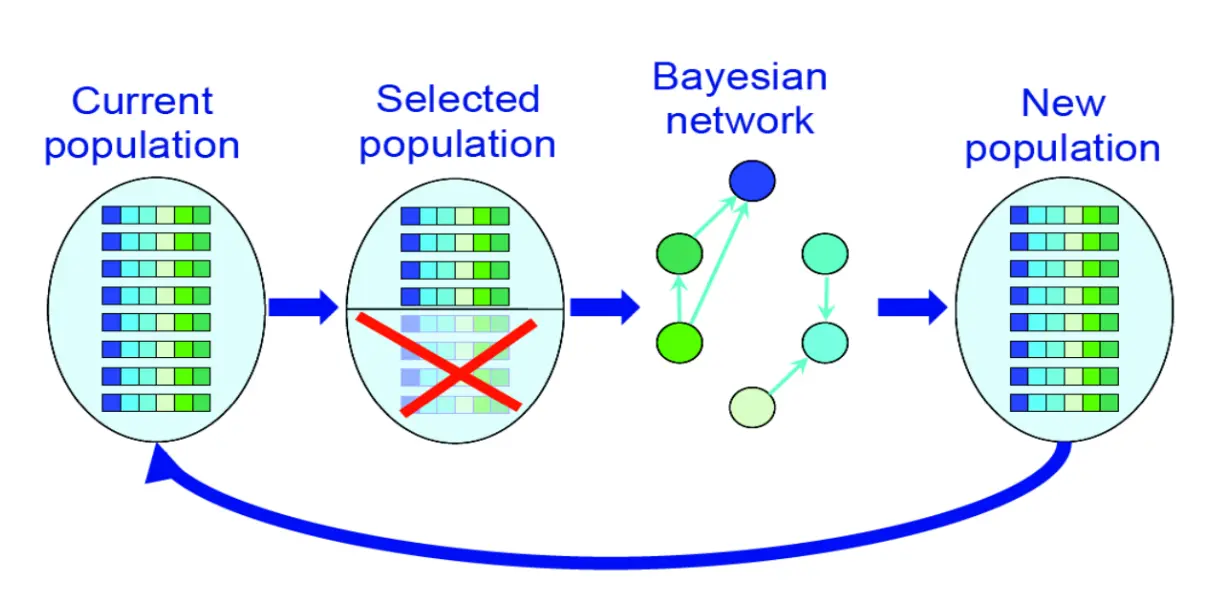 
- 关键步骤：
- 不是统计单个bit的概率（UMDA做法）
- 而是学习一个贝叶斯网络，这个网络描述bit之间的依赖关系。
- 这个网络告诉你：“某个bit的取值，可能和另一个bit的取值有关”。
- 这是BOA最核心的创新点：自动学习bit之间的依赖结构，不需要你提前知道。
Genetic Programming
动机问题 Symbolic Regression
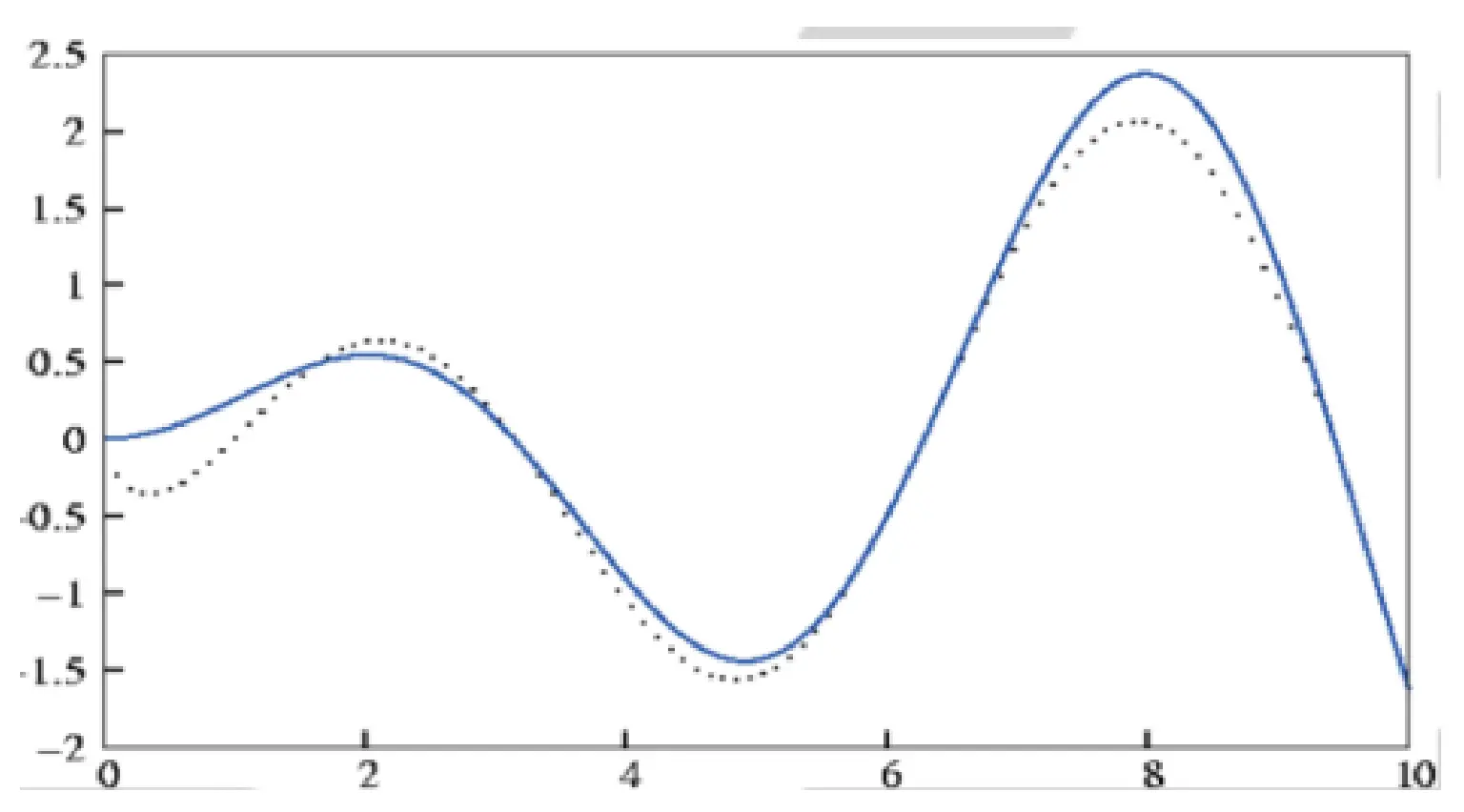这个问题就是，给你一连串点，你需要找到一个function让其尽可能拟合所有点。 而这种问题一般用树的符号表示： 
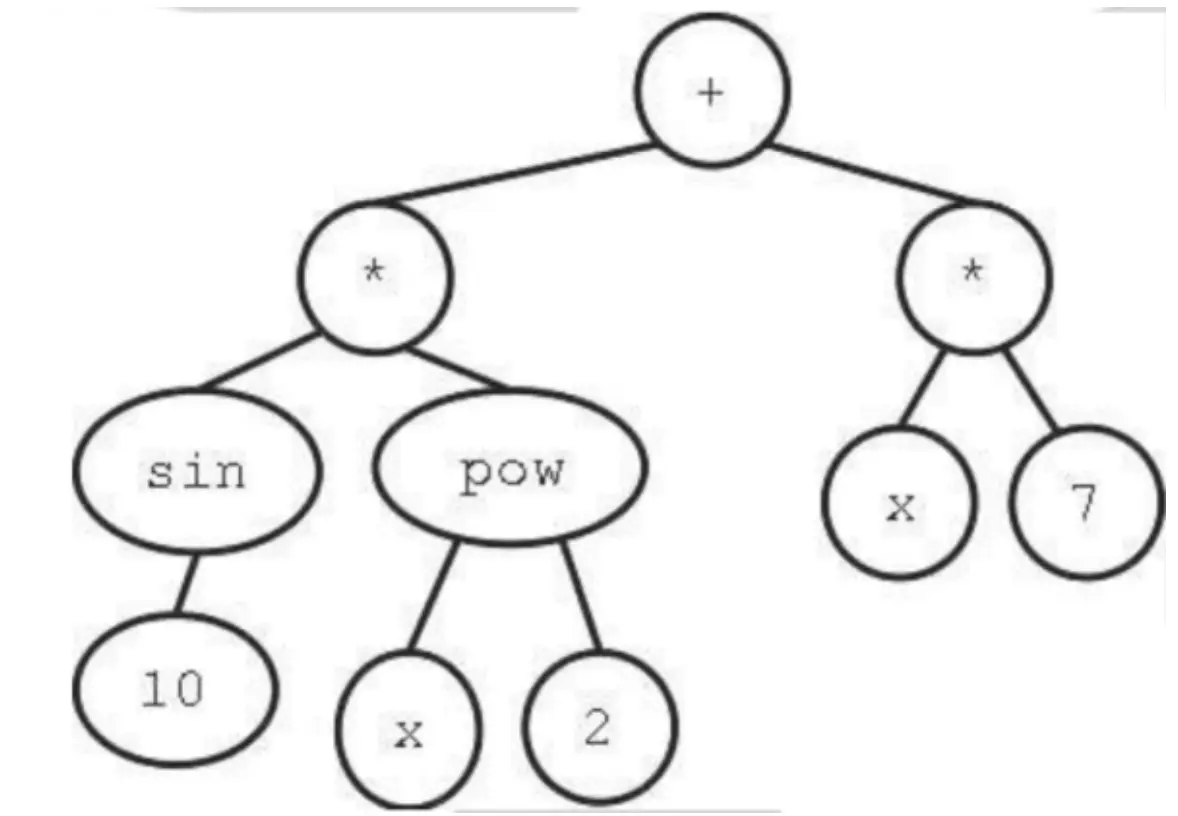这就是一个前缀表达式。我们可以看到，里面的函数叫做function set, 那些数字，也就是参数，叫做terminal set
在Terminal Set中，有几个概念。Arity意思是函数的参数量，Terminal Set的Arity应该是0. 而对于function set，定义域需要能够处理所有输入。
Crossover
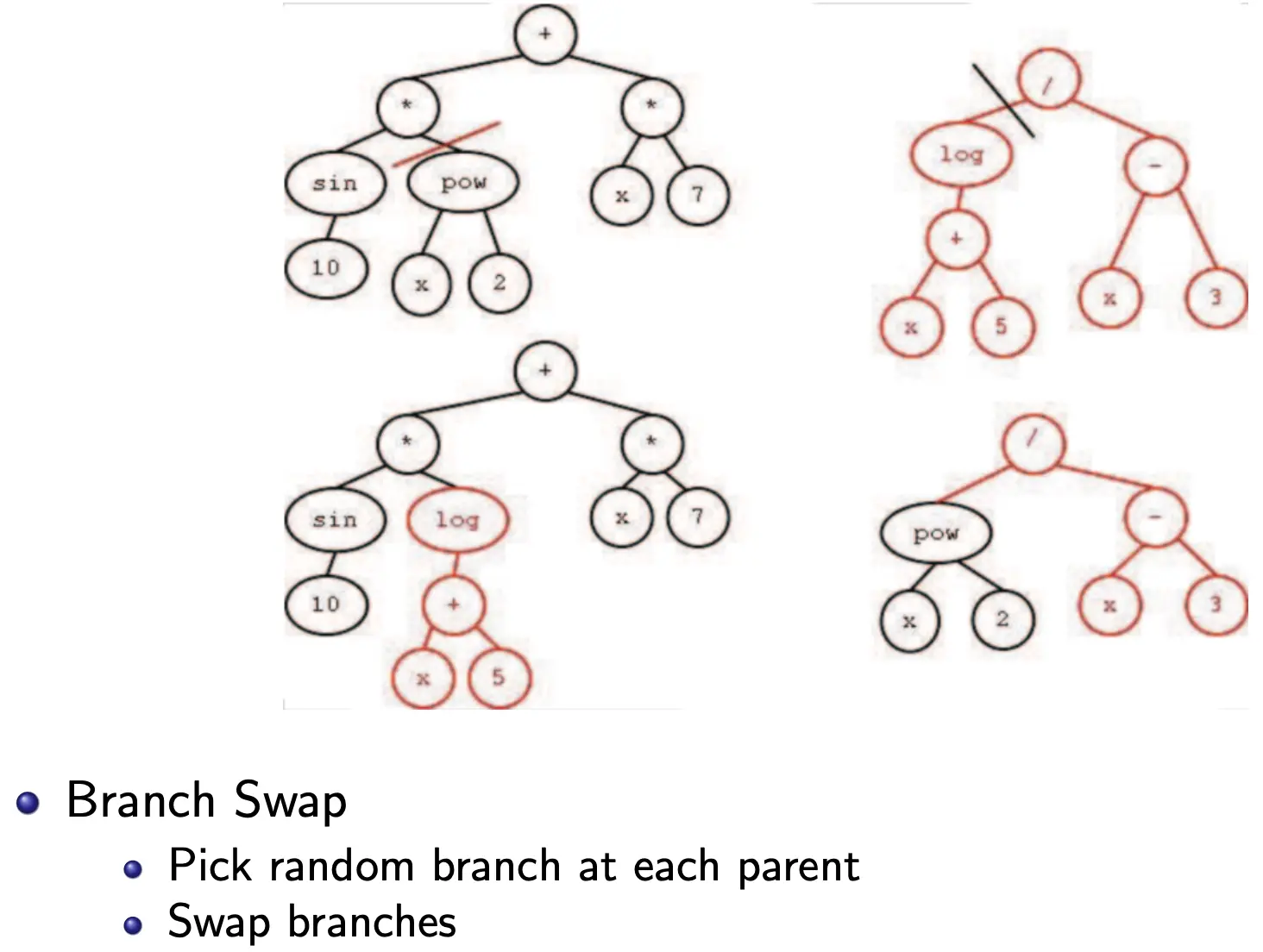
这里还有一种特殊的CrossOver，叫做Match 1-Point Crossover。其思想在于，交换的部分形状应当是一样的。这是通过arity判断的。
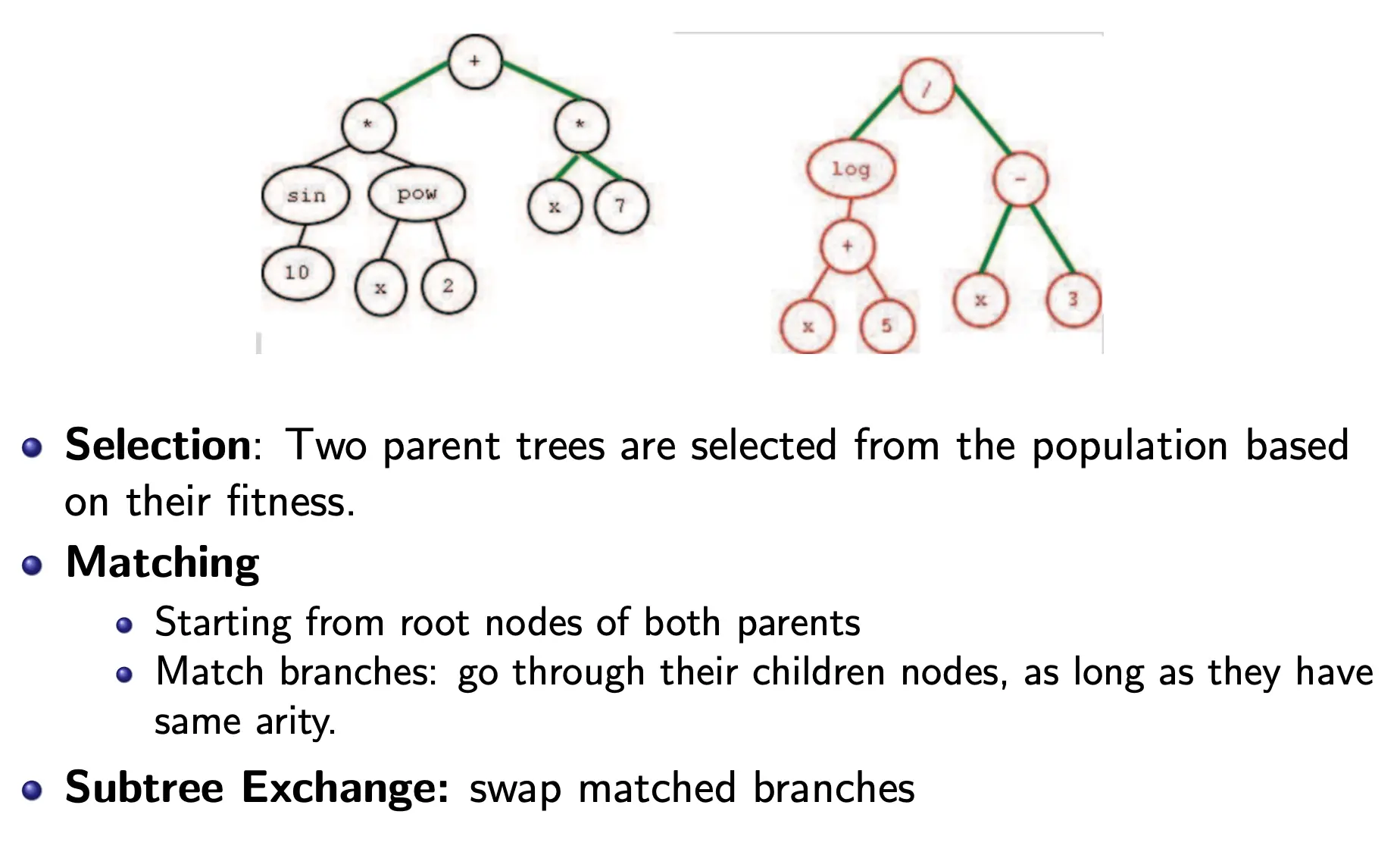
Mutation
从父节点中随机选择一个分支后删除该分支，用随机新分支替换（新分支创建方式与初始种群创建方式相同）。
初始种群创建
如何创建初始种群呢？有3种方法：
Full Method
把树的深度固定为treeDepth，然后随机生成函数节点，直到所有分支都达到treeDepth-1 之后给所有的分支随机添加Terminal Set 这样生成的树每条路径长度一样，适合保证初始种群复杂度，但缺乏深度多样性。
Growth Method
生成树的深度最多不超过 maxDepth。
- 随机生成函数节点或终端节点，直到所有分支都已经是终端节点，或是已经达到**(maxDepth - 1)**的深度。
- 给所有还没有终端节点的分支补充随机终端节点。
Ramped Half-and-Half
设定最大树深度maxDepth和种群大小popSize。 对每个树深度n = 2 到 maxDepth：
- 一半个体用Growth Method生成深度为n的树；
- 另一半个体用Full Method生成深度为n的树。
Bloat问题
由于不均匀的交叉操作（Crossover），导致个体在进化中越变越大。这会使计算变慢，冗余。 解决方法：
- 惩罚程序大小
- 使用Match one point crossover
线性GP
除了用树，也可以用线性结构描述程序
- Register Machine Programming：状态机 + 汇编语言
- Van-Neumann Architecture：参考冯·诺依曼架构，程序和数据存放在同一个线性空间里。
- String Representation：每个个体是一个指令序列，所以是线性字符串形式，而不是树。 交叉就是直接对字符串做单点或双点交叉，变异就是替换某个指令（随机换一个指令），还可以新增删除指令。
图GP
图也可以表示进化编程。因为是图结构，天然支持回到之前的节点，形成循环，递归。
- 每个节点都是一个操作，操作数来自一个栈。计算结果也会压回栈中。
- 边定义了控制流，比如，根据栈里的某个值，大于0走A边，等于0走B边，小于0走C边。 但是在交叉互换和变异的时候就必须要考虑到图的特殊性，比如说交叉时要保持图的连通性，变异可能会增加 / 删除边，节点。
Evolving graphs by graph programming (EGGP)
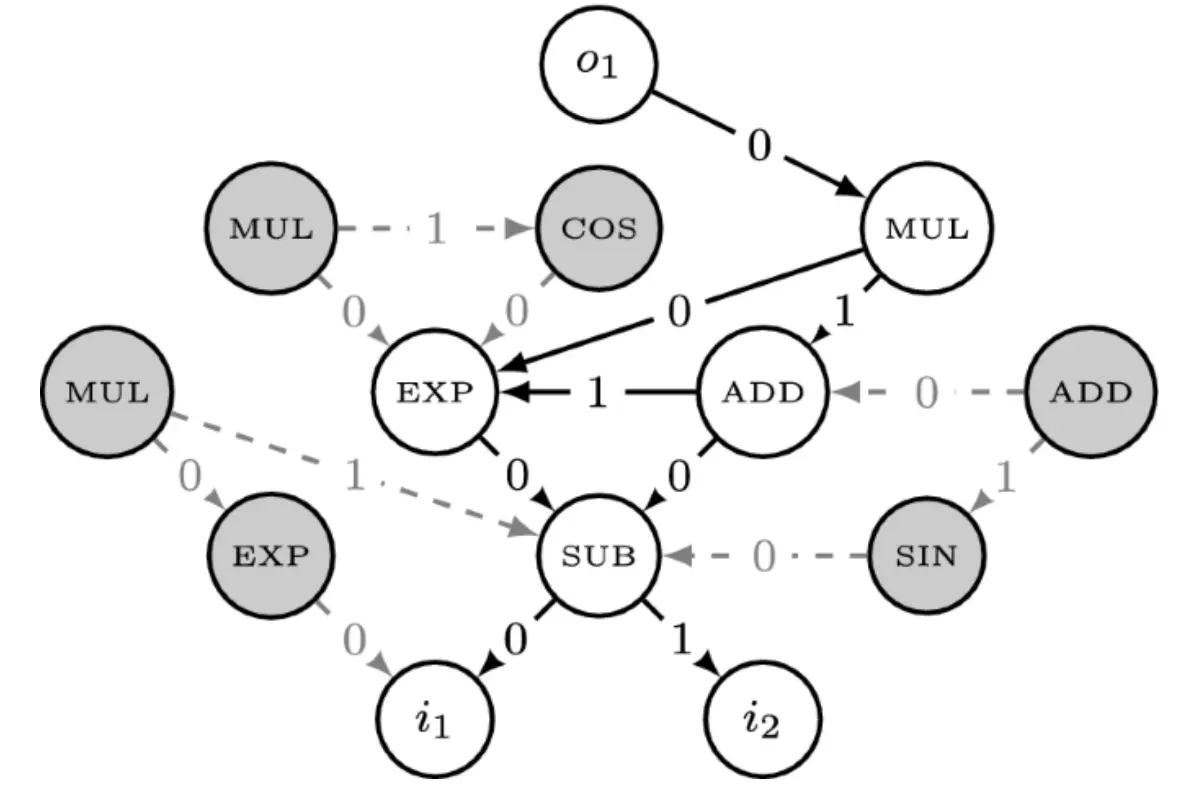是DAG（有向无环图）
- 输入节点：代表问题输入（输入变量、传感器读数等），只能出边，不能入边。
- 输出节点：代表问题的输出（预测结果等），只能入边，不能出边。
- 函数节点：代表运算/逻辑操作，连接其他节点。
对于边，函数节点的每个参数位置，都有一个专属的出边。这些出边有顺序和标签（区分第几个参数）。
然而，在图中可能会有一些没有连到输出节点的Neutral Nodes，这些节点并不影响fitness，但保留在结构里，后期可以提供搜索空间，相当于增加了冗余度，是备胎。
在这个图里，边的编号从0开始，每个函数节点的输入参数由编号的边指定。
- 例如SUB这个节点，它是个二元操作，有两个输入：
- 第0个输入是 i1；
- 第1个输入是 i2；
- 这个SUB节点表示的就是i1−i2。
Larry Shi