Linear Regression

标签

ML

AI

字数

412 字

阅读时间

2 分钟

本节来介绍基于最小二乘法的线性回归。

情景描述

真实的x，y存在这样的关系：

$$y=f(x,\omega )+ϵ$$

其中，f(x,w) 是基准的线性，epsilon是固有噪音，这玩意没法确定。有了这个噪音，你的真实标签看起来就是这样的：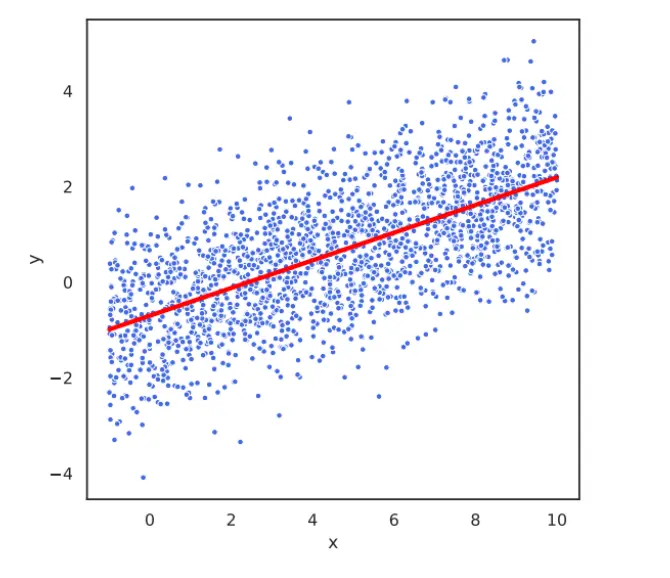

度为1的OLS

degree为1，说明w只有一个，外带一个截距。所以我们假设目标函数是这样的：

$${\hat{y}}_i={\omega }_0+{\omega }_1{x}_i$$

那么损失如果用MSE的话，就是这样的：

$$R(\omega )=\sum _{i=1}^N{r}_i^2=\sum _{i=1}^N(y_i-{\hat{y}}_i(x_i,\omega ){)}^2$$

为了最小化损失，所以求导：

$$\begin{array}{rl}\frac{\partial R({\omega }_0,{\omega }_1)}{\partial {\omega }_0}& =0\\ \frac{\partial R({\omega }_0,{\omega }_1)}{\partial {\omega }_1}& =0\end{array}$$

求导得到的结果如下：

$$\begin{array}{c}\sum _{i=1}^N{x}_i{y}_i={\omega }_0\sum _{i=1}^N{x}_i+{\omega }_1\sum _{i=1}^N{x}_i^2\\ \sum _{i=1}^N{y}_i={\omega }_{0}N+{\omega }_1\sum _{i=1}^N{x}_i\end{array}$$

写成矩阵形式就是这样：

$$(\begin{array}{c}\sum _i^N{x}_i{y}_i\\ \sum _i^N{y}_i\end{array})=\left(\begin{array}{cc}\sum _i^N{x}_i& \sum _i^N{x}_i^2\\ N& \sum _i^N{x}_i\end{array}\right)\left(\begin{array}{c}{\omega }_0\\ {\omega }_1\end{array}\right)$$

解就是这样：

$$\left(\begin{array}{c}{\omega }_0\\ {\omega }_1\end{array}\right)={\left(\begin{array}{cc}\sum _i^N{x}_i& \sum _i^N{x}_i^2\\ N& \sum _i^N{x}_i\end{array}\right)}^{-1}\left(\begin{array}{c}\sum _i^N{x}_i{y}_i\\ \sum _i^N{y}_i\end{array}\right)$$

任意degree OLS

定义目标函数为这样：

$${\hat{y}}_i(x_i,\omega )=\sum _{i=0}^M{\omega }_j{\varphi }_j(x_i)={\omega }^T\varphi (x_i)$$$$\mathit{\omega }=\left(\begin{array}{c}{\omega }_0\\ {\omega }_1\\ \\ {\omega }_M\end{array}\right),\varphi =\left(\begin{array}{c}{\varphi }_0(x_i)\\ {\varphi }_1(x_i)\\ \\ {\varphi }_M(x_i)\end{array}\right)$$

其中phi是非线性变化，phi0(xi) = 1。 求导为0得到结果：

$$\begin{array}{rl}\frac{\partial R(\mathit{\omega })}{\partial \mathit{\omega }}& =\sum _{i=1}^N(y_i-{\mathit{\omega }}^T\varphi ({\mathit{x}}_i))\varphi ({\mathit{x}}_i{)}^T=0,\\ \\ \sum _{i=1}^N{y}_i{\varphi }^T(x_i)& ={\mathit{\omega }}^T(\sum _{i=1}^N\varphi (x_i){\varphi }^T(x_i))\end{array}$$

如果我们记 design matrix $\mathrm{\Phi }$为：

$$\mathbf{\Phi }=\left(\begin{array}{cccc}{\varphi }_0(x_1)& {\varphi }_1(x_1)& \cdots & {\varphi }_M(x_1)\\ {\varphi }_0(x_2)& {\varphi }_1(x_2)& \cdots & {\varphi }_M(x_2)\\ & & & \\ {\varphi }_0(x_N)& {\varphi }_1(x_N)& \cdots & {\varphi }_M(x_N)\end{array}\right)$$

那么上面的带求和的式子就可以写为：

$${\omega }_{OLS}=({\mathbf{\Phi }}^T\mathbf{\Phi }{)}^{-1}{\mathbf{\Phi }}^T\mathbf{y}$$

然而，由于 $\mathrm{\Phi }$ 很大的时候，其逆很难算。所以在适当时你应该使用 梯度下降。 当梯度下降时，你可以用这些cost function:

非线性嵌入

这里介绍四种非线性嵌入：

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update