Overfitting
字数
471 字
阅读时间
2 分钟
过拟合会有很差的泛化性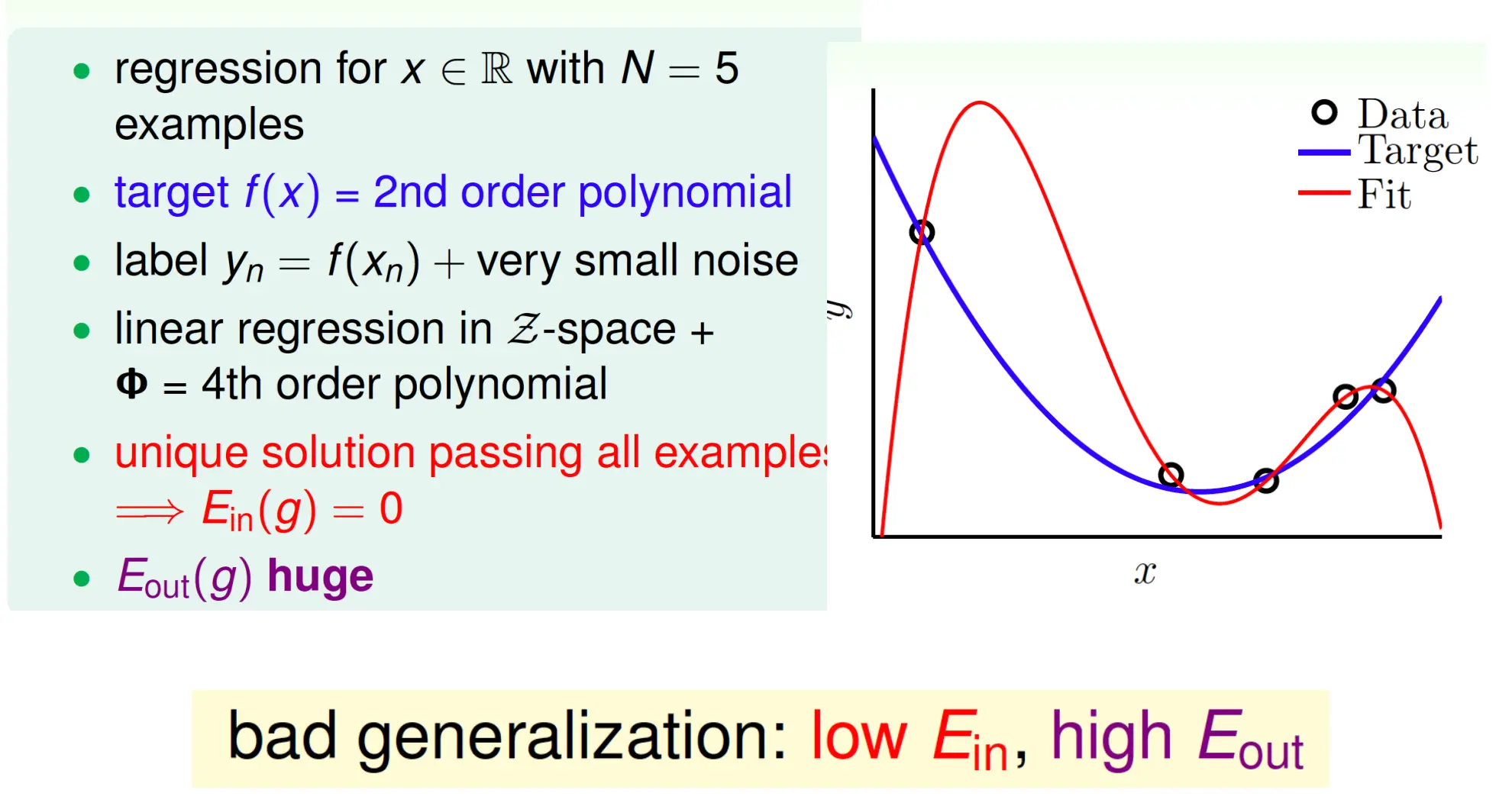 
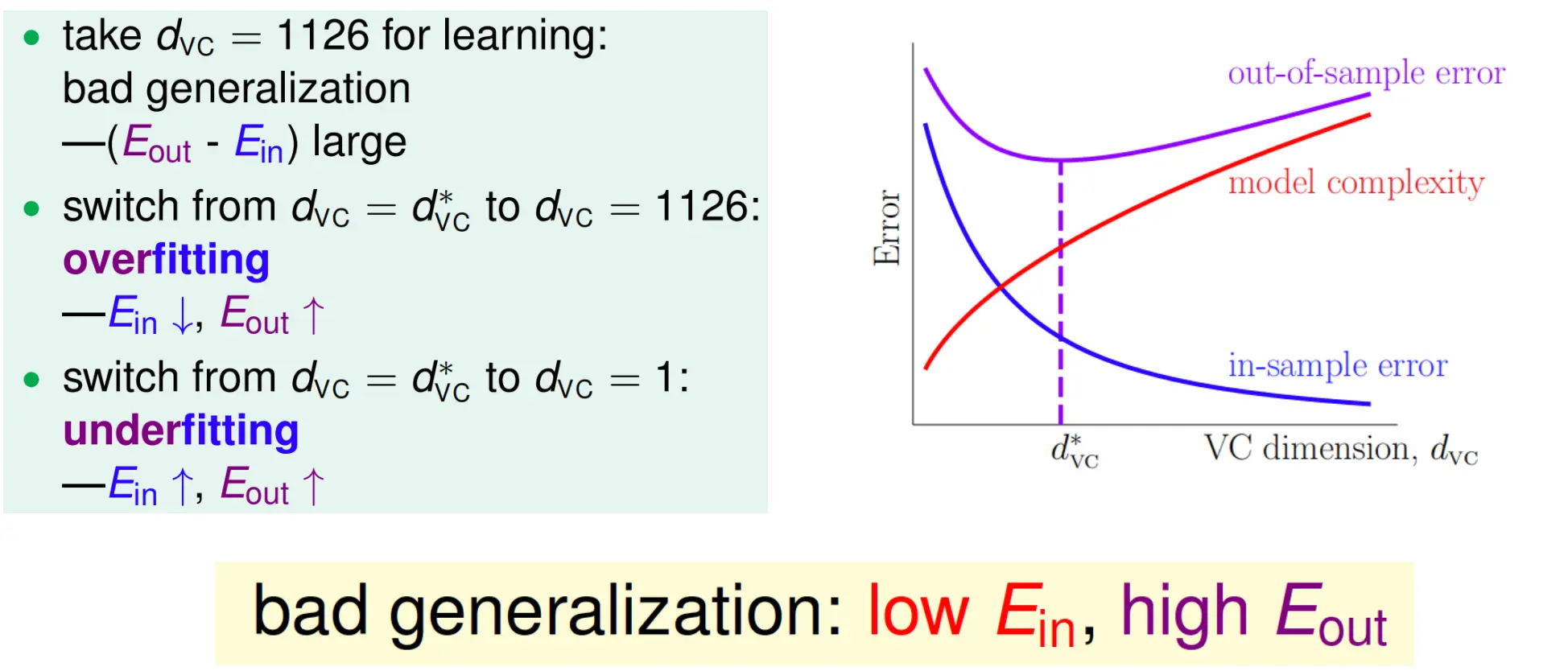
Factors
如果我们把目标函数抽象成一个多项式，那么整个标签就变成了：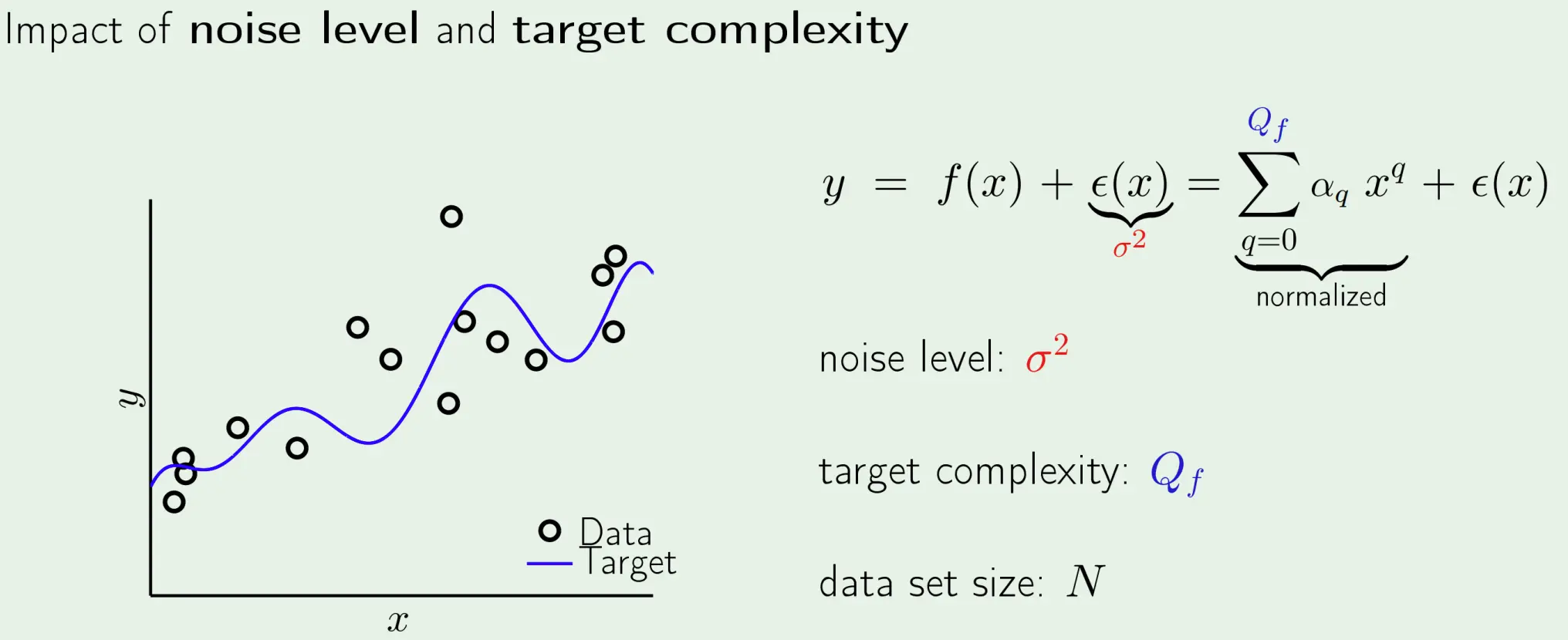 
那么我们需要学习的函数就是fx，也就是那个多项式，而需要克服的是噪音。 我们要探究噪音等级sigma，目标模型复杂度Q以及数据量N对过拟合的影响。
我们首先定义一个过拟合metric。我们给定一组点，然后用H2和H10去测量Eout。 于是我们定义metric为：
如果这个metric大于0，那么就是过拟合
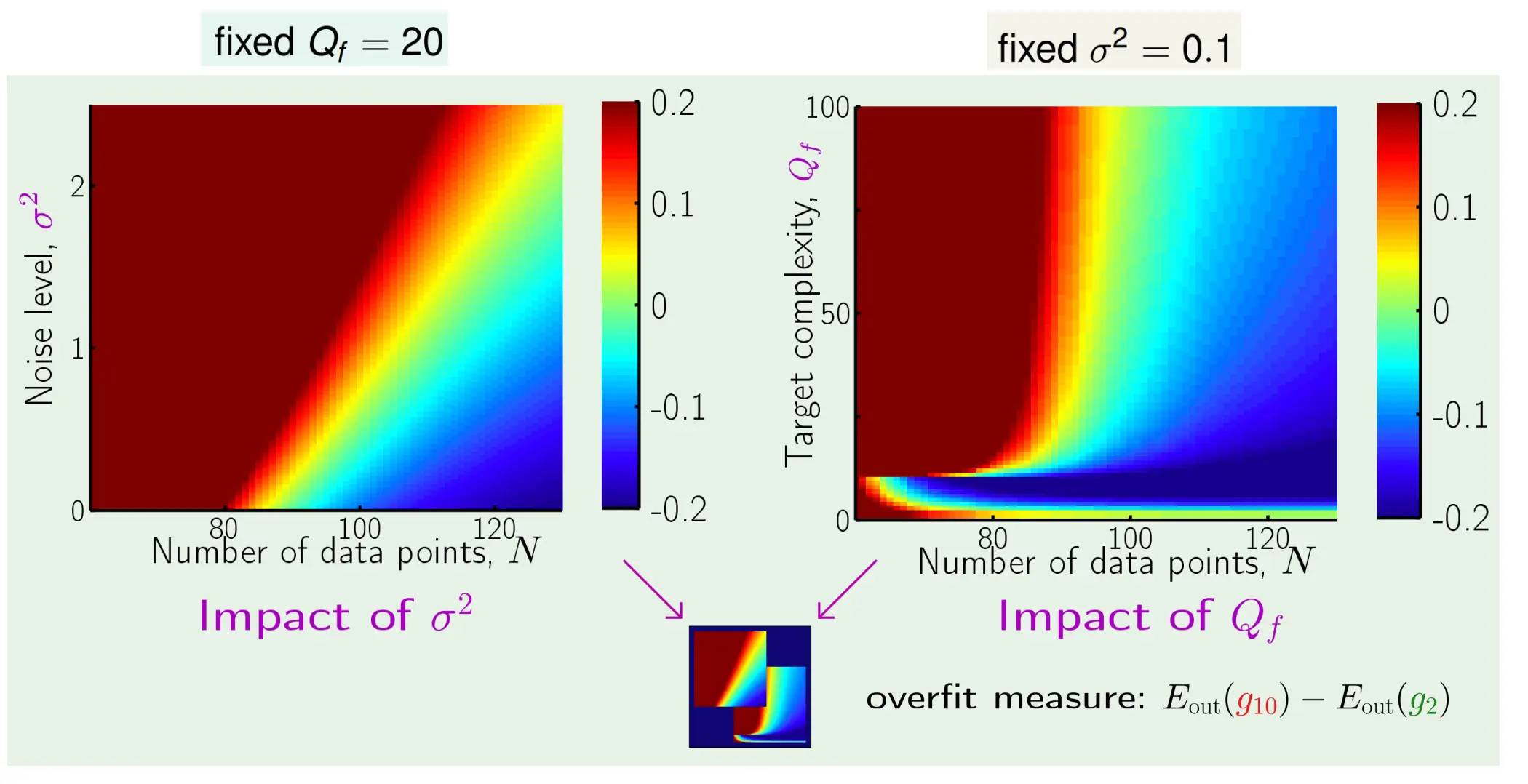可以看到，当目标模型复杂度Q（固定性噪声）固定的时候，噪音越大越容易过拟合，数据越少越容易过拟合 当噪音大小固定时，数据越少越容易过拟合，目标模型复杂度Q越大是越大越容易过拟合
所以有，样本少，固定噪音（目标模型复杂度）大，随机噪音大，学习的模型容量大，容易过拟合。
MLE/OLS不能防止过拟合
在 Gaussian‑noise 假设下，MLE = OLS，但只有最小化训练误差的目标会导致对高容量模型的过拟合。要真正防止过拟合，需要在 MLE 基础上加入正则化或先验。
贝叶斯回归可以防止过拟合
贝叶斯回归通过先验+似然得到后验，不仅拟合了数据，还自然地抑制了过拟合，并且用后验分布刻画了参数估计的不确定性。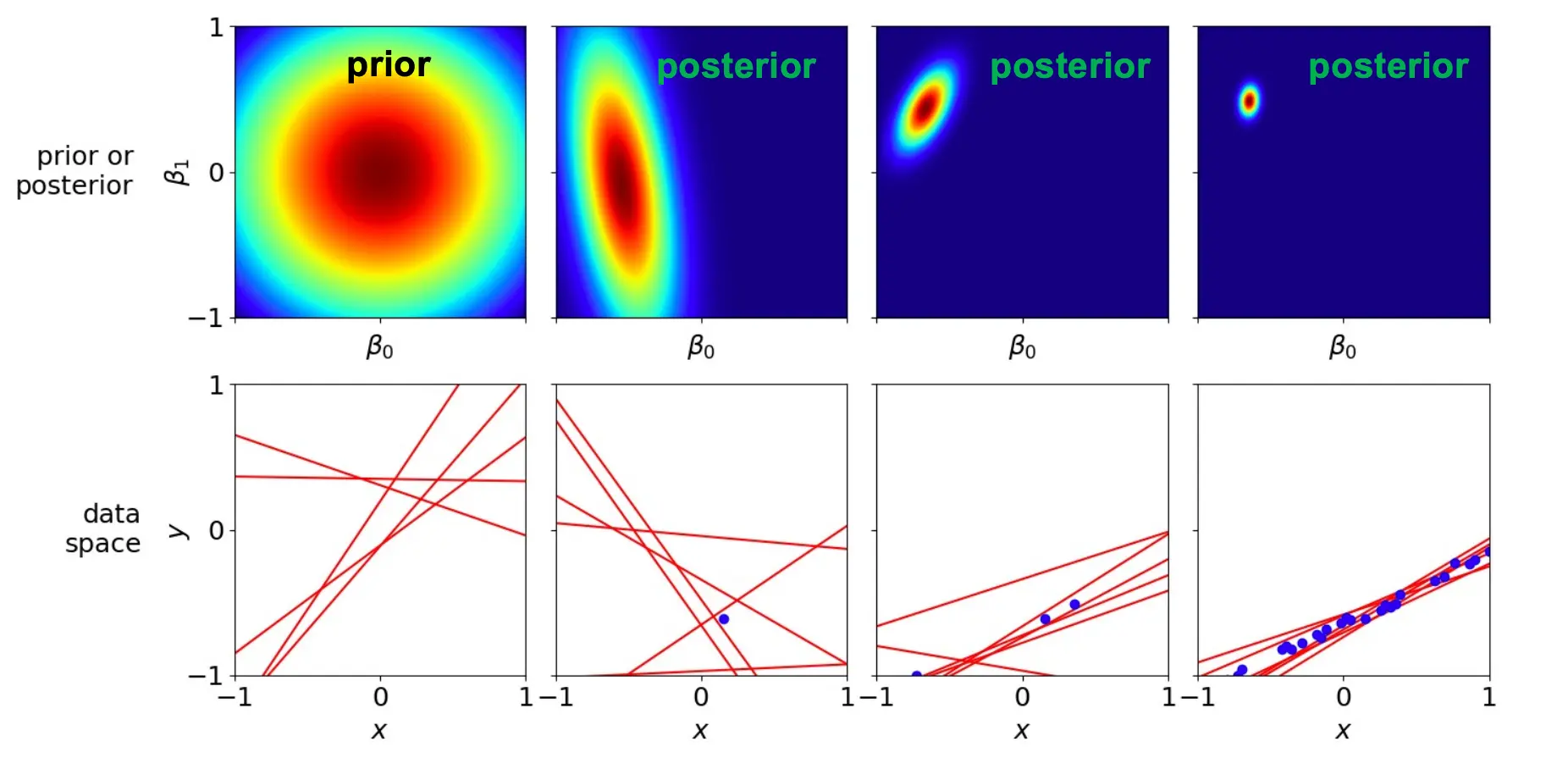 
克服过拟合的方法
Regularisation: Putting the brakes Cross-Validation: Checking the bottom line
Larry Shi