GNN

标签

AI

DL

ML

Graph

字数

2144 字

阅读时间

9 分钟

图介绍

图无处不在，比如说在社交媒体，在网络中，药物设计中，蛋白质中都存在。 很多现代的神经网络通常处理的内容都能转化成图。比如说，图像就是图grid, 文本语音就是线性序列结构。图的优势就是可以转化为任意大小和拓扑结构的数据。 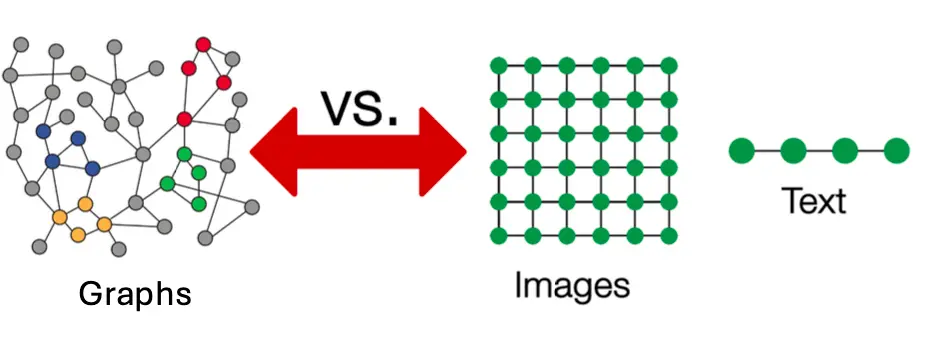这里有对图的介绍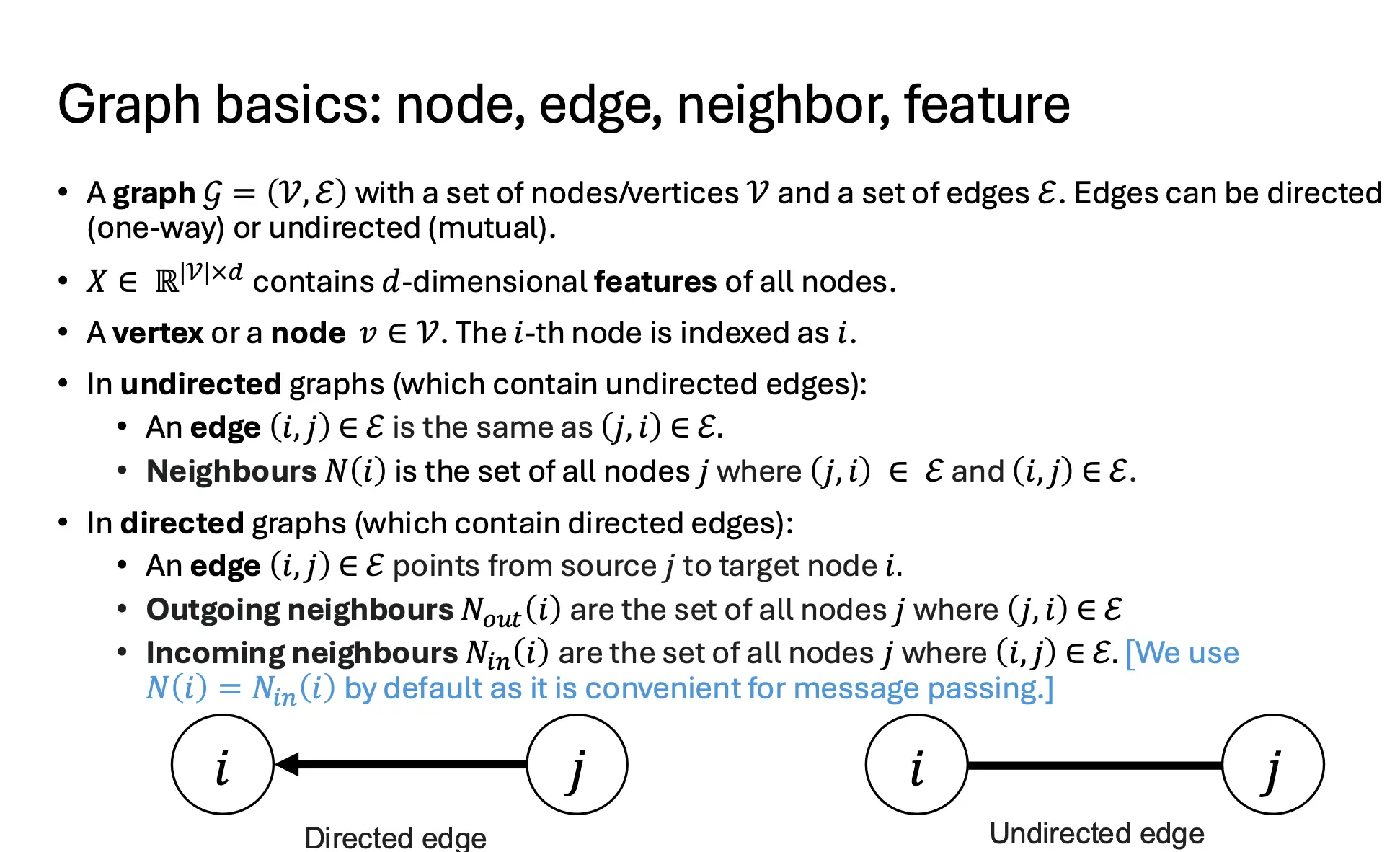： 其中，Outgoing neighbors Nout(i) 为节点 i 的出邻居集合，表示从 i 指向的节点集合 j，满足 (i,j)∈E Incoming neighbors, Nin​(i) 节点 i 的入邻居集合，表示指向 i 的节点集合 j，满足 (j,i)∈E

你可以用矩阵表示有向图，无向图（对角对称），带权重图（有向图的1变成权重）。

GNN 任务初识

NOTE

其实，GNN的精髓在于消息传播。我们认为，GNN每一个节点都有自己的向量表示，比如说，我本人年龄22，性别男，那么我的向量就会是 [22, 0], 而我的邻居可能是年龄21，性别女，那么她的向量就是 [21, 1]. 而消息传递就是，设计一个函数，让和你有联系的节点的向量影响你的向量。比如说，消息传递是hi = (2xi + xj) / 3, 那么我的隐藏表示状态hi就是 ([22, 0] * 2+ [21, 1]) / 3 = [21.67, 0.33]. 这个隐藏状态就表示了，我大概率是一个21 22岁的人，而我自己是个男的，但是周围也有一些女的。这就相当于是一个集合信息。这时，你只需要设计一个分类网络，比如说简单的全连接层，把hi作为输入，就可以通过这个高维的隐藏表示来判断我本人的一些信息。 真实任务中，可能也会在消息传递后做一些池化之类的。 实际上，消息传递得到的最终H，可以看作是一种Embedding。

节点分类

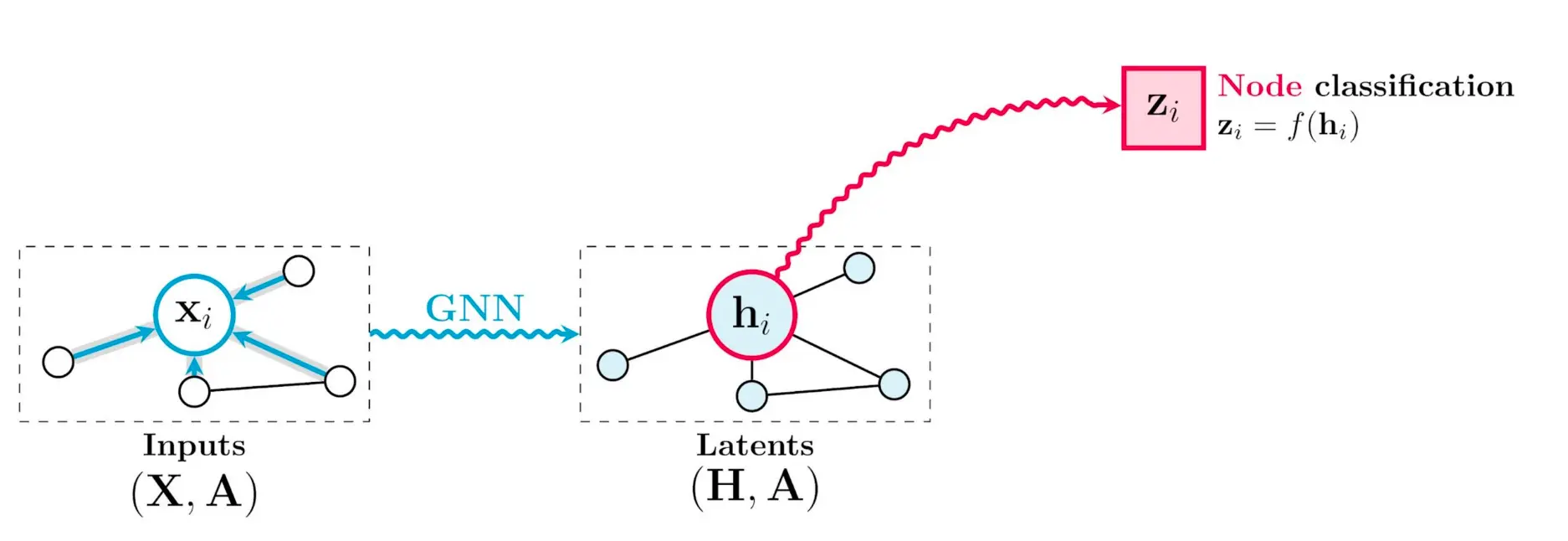
图分类

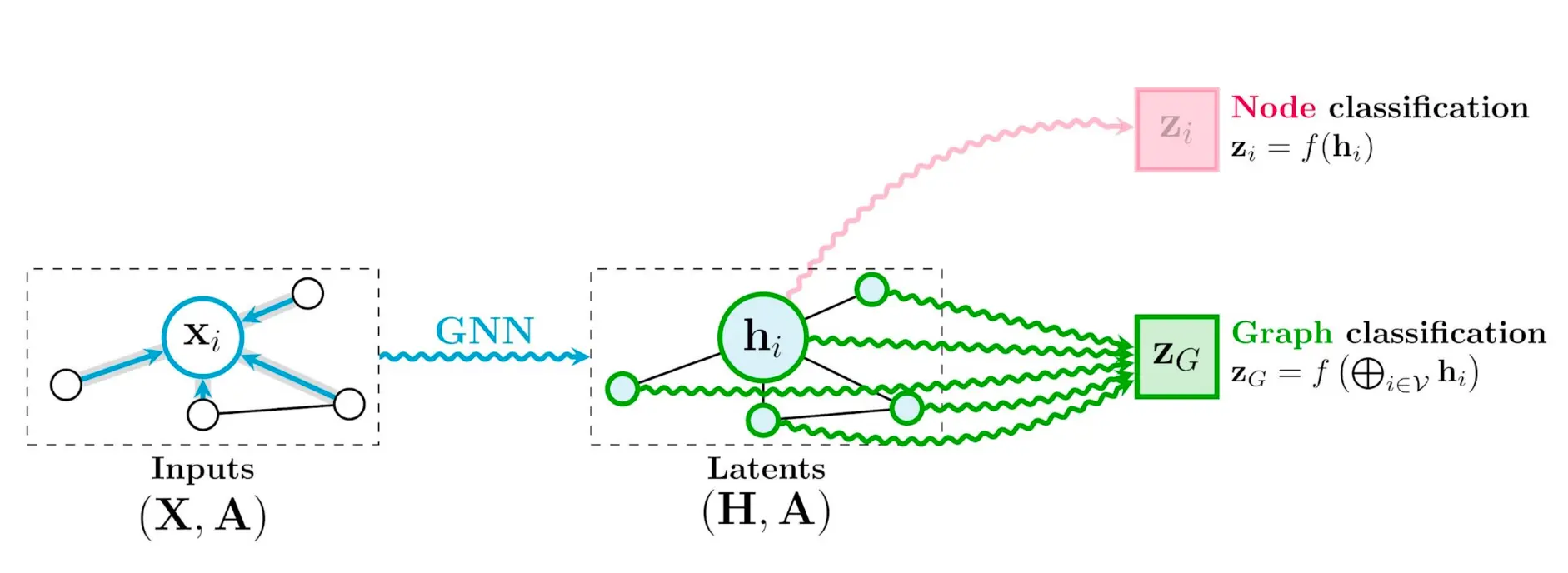
连接预测

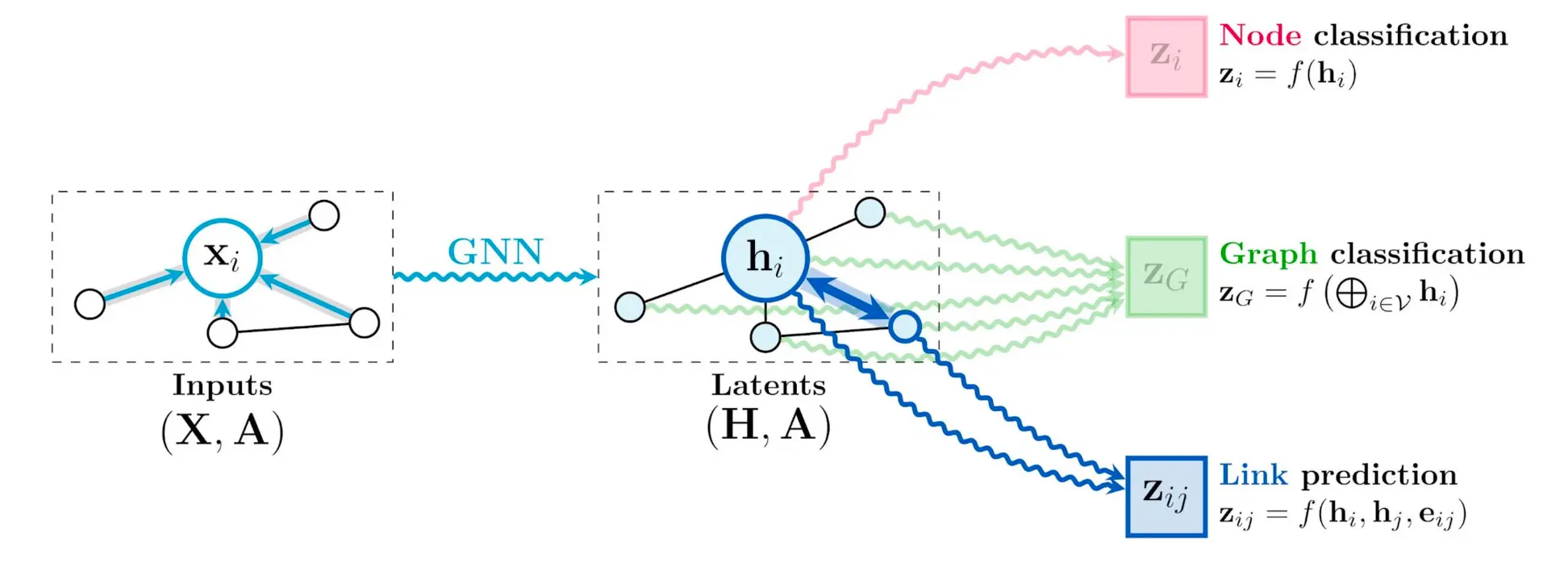
有时会做池化

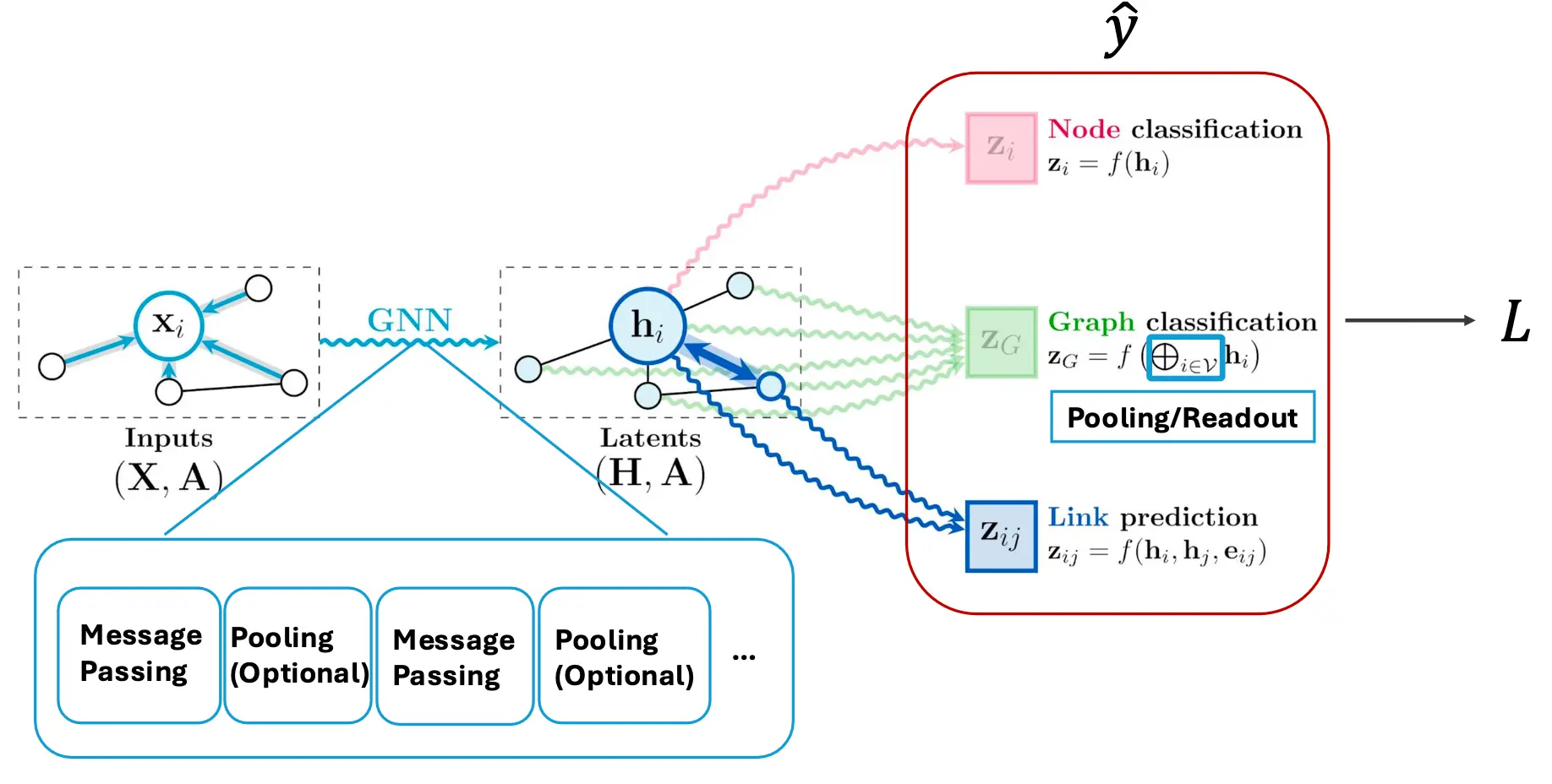
Message Passing

一般形式介绍

首先是一个toy example. 在了解了什么是消息传递后，这很好理解。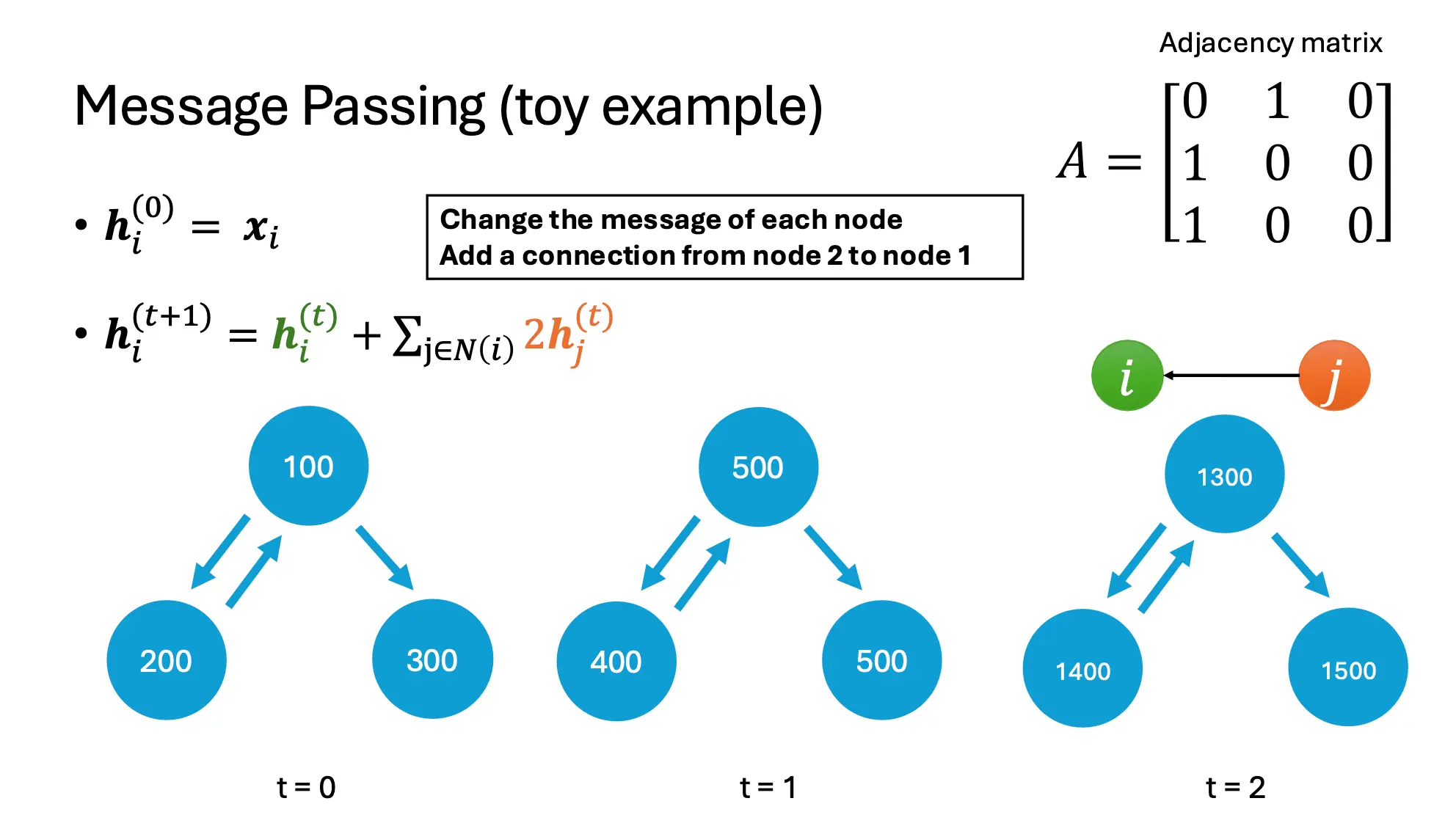

如果我们把 $h_i^{(t+1)}=h_i^{(t)}+\sum _{j\in N(i)}2h_j^{(t)}$ 这个例子拆解开来看，就是这样的：

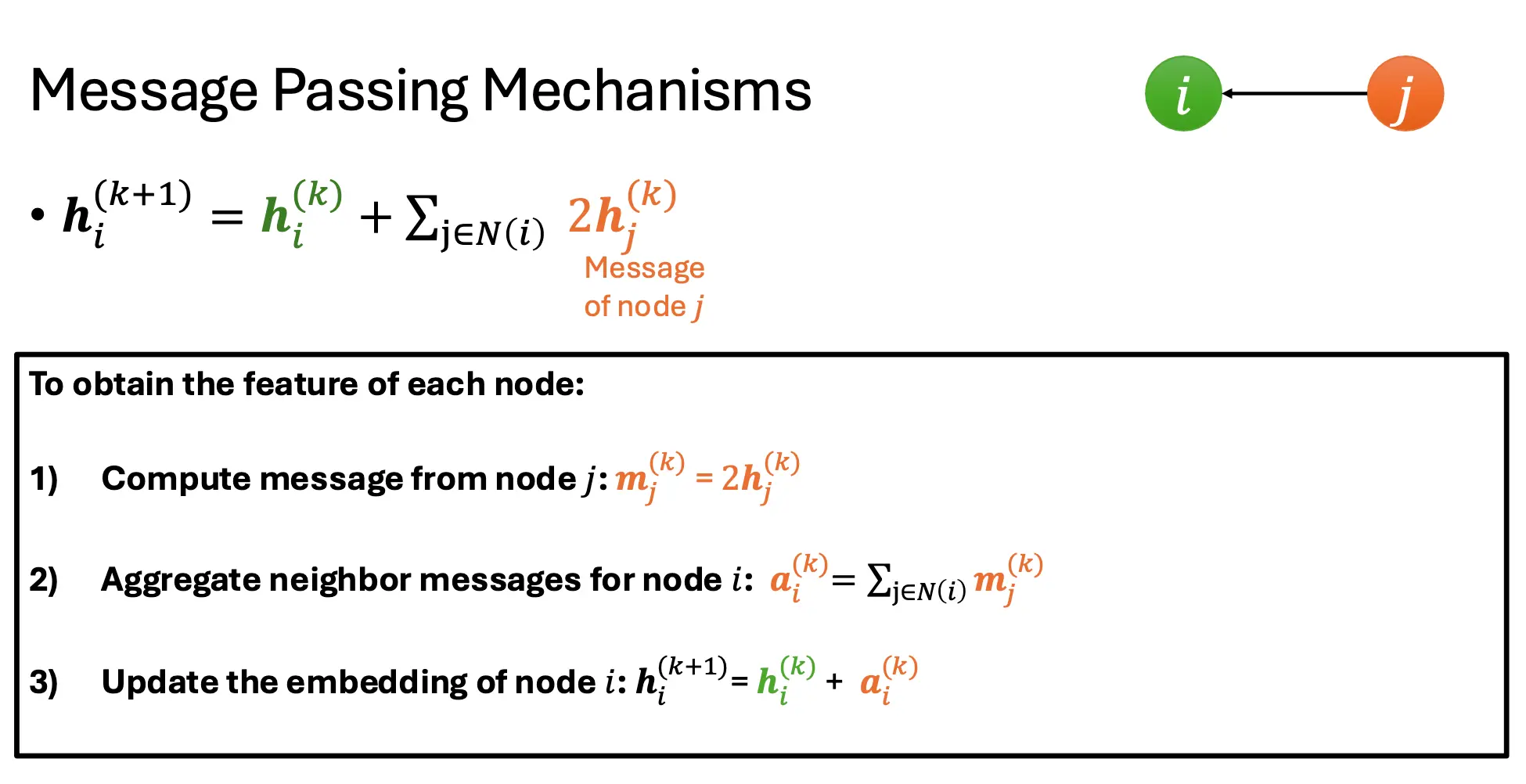
这个消息传递的式子，可以看作两部分，左边的hi是自己的隐藏向量，而右边的那一堆，相当于是相邻节点带来的信息。 在这个例子中， $m_j^{(k)}=2h_j^{(k)}$ 就相当于是把某一个邻接节点的h转化成信息m。 接着，聚合所有的邻接信息。$a_i^{(k)}=\sum _{j\in N(i)}{m}_j^{(k)}$ 最后，中心节点根据聚合的邻接信息，来更新自己的隐藏向量。$h_i^{(k+1)}=h_i^{(k)}+a_i^{(k)}$

如果总结出一个更一般的形式，就是这样的：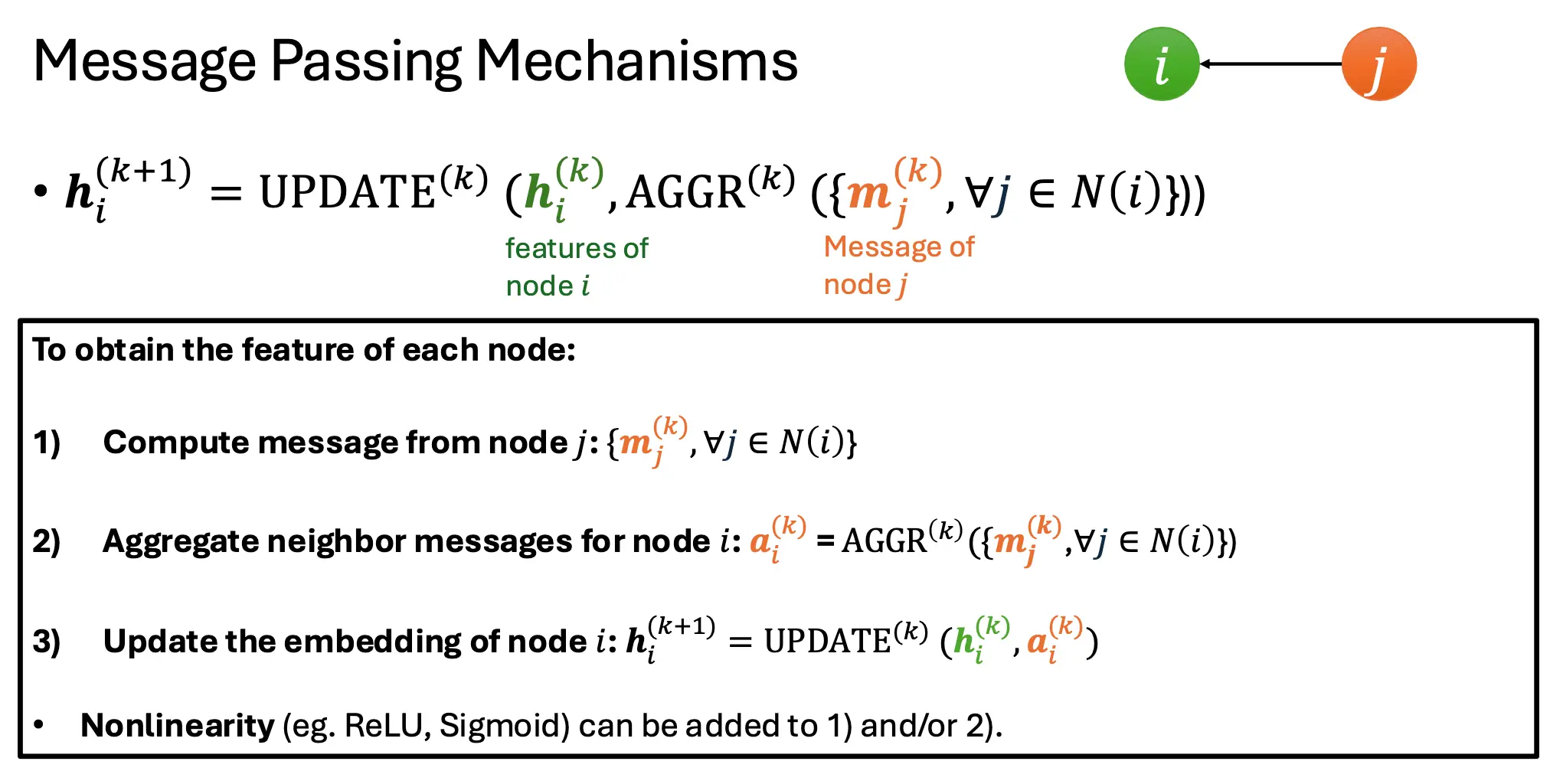

GCNConv

首先，我们介绍一个Graph Convolution Network的message passing的设计。

$${\mathit{h}}_i^{(k+1)}=\sigma \left(\sum _{j\in \{i\}\cup N(i)}\frac{e_{ij}}{\sqrt{{\hat{d}}_i{\hat{d}}_j}}{\mathrm{\Theta }}^{\mathrm{T}}{\mathit{h}}_j^{(k)}\right)$$

其中 ${\hat{d}}_i=1+\sum _{j\in N(i)}{e}_{ij}$ 是添加了自我回环之后的节点度。 $e_{ij}$ 是 j 指向 i 的边权重。 ${\mathrm{\Theta }}^T$ 代表了一个线性变化的矩阵，这个矩阵在一切过程中是共享的（卷积），$\sigma$ 是激活函数。 在这里面，信息计算的公式是$m_j^{(k)}={\mathrm{\Theta }}^{\mathrm{T}}{h}_j^{(k)}$ ，是根据hj独立算出的。 而聚合是加权的，权重为 $c_{ij}=\frac{e_{ij}}{\sqrt{\widehat{d_i}\widehat{d_j}}}$ . 这个分母是一个归一化项，确保了一个度数很高的节点不要主导了整个网络的信息传递。

这个网络对Cora数据集进行了嵌入的工作，并对其进行了分类。

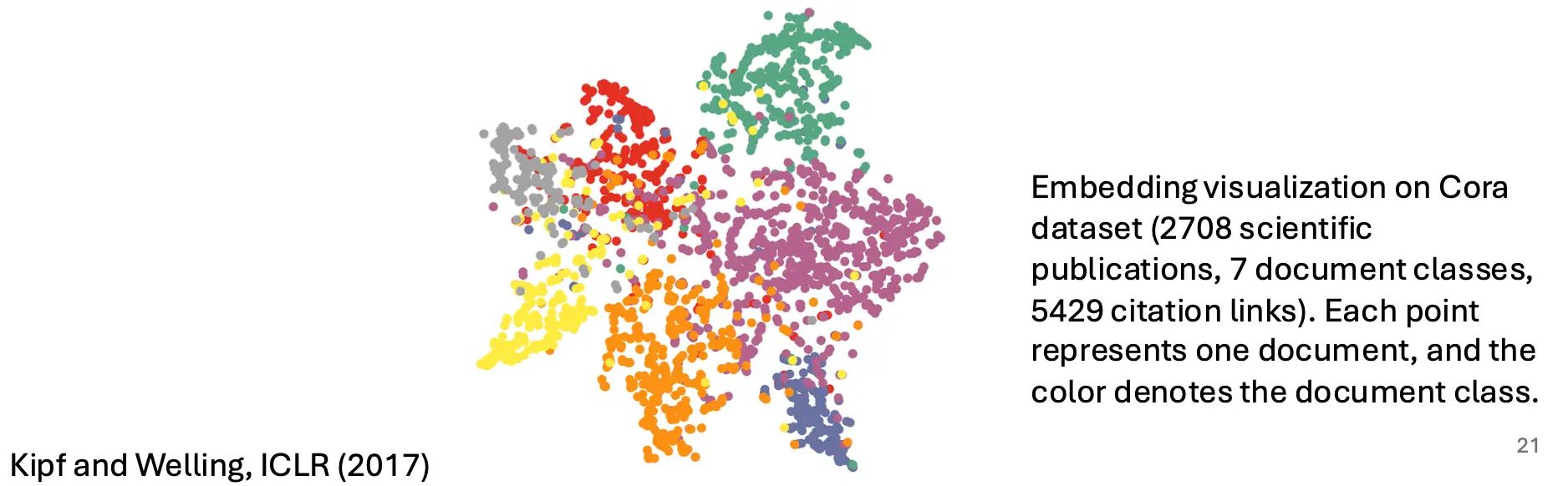这里就体现出来，图神经网络最后得到的H隐藏向量，其实是可以作为一种embedding去使用的。得到嵌入之后，后面的分类器就可以对其进行很好的分类。

EdgeConv

$${\mathit{h}}_i^{(k+1)}=\sigma \left(\sum _{j\in N(i)}{\mathrm{MLP}}_{\mathrm{\Theta }}({\mathit{h}}_i^{(k)}\parallel ({\mathit{h}}_j^{(k)}-{\mathit{h}}_i^{(k)}))\right)$$

其中 || 代表着向量连接。 这里面信息 是根据hi和hj通过神经网络算出来的。

$$m_j^{(k)}={\text{MLP}}_{\mathrm{\Theta }}(h_i^{(k)}\parallel (h_j^{(k)}-h_i^{(k)}))$$

而聚合过程就是加和。这个网络的图示是这样的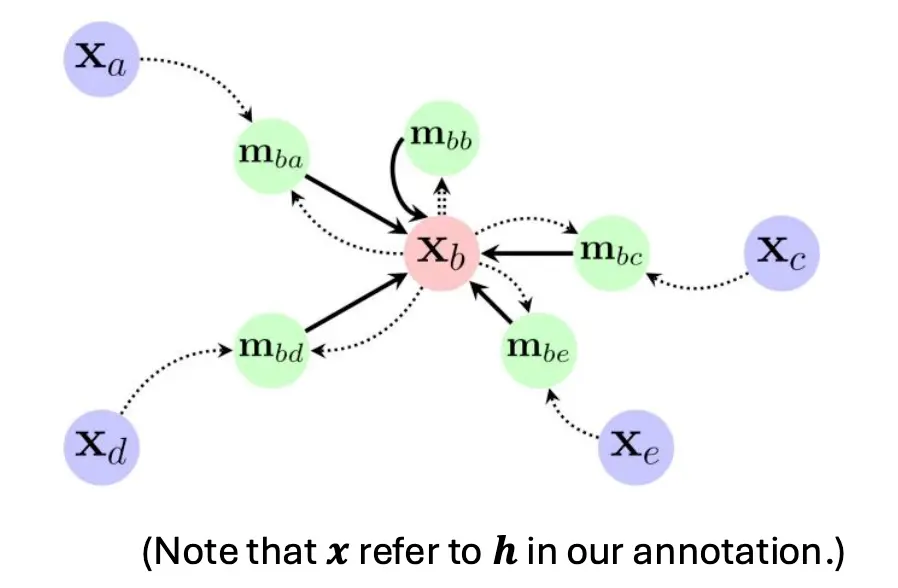： EdgeConv还有一种变体叫做DynamicEdgeConv。其特殊性在，上面的N(i)并不是固定的，而是通过每次计算hi之后通过计算相似度计算出来的。相当于动态计算了图关系。 EdgeConv可以做点云分割：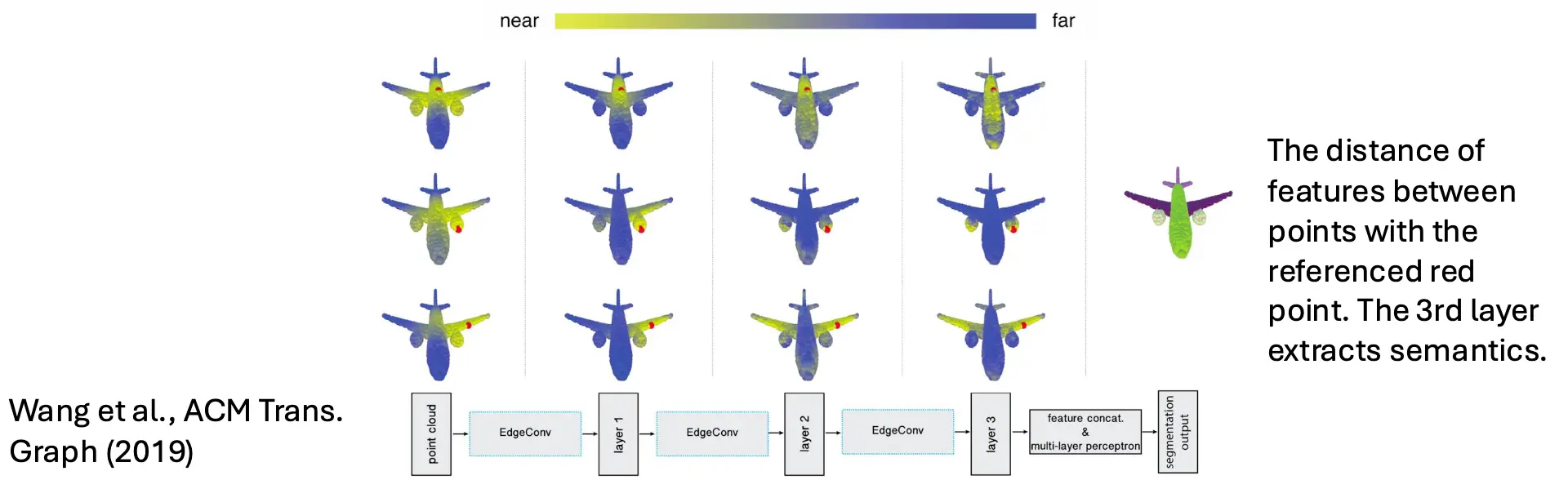

形式总结

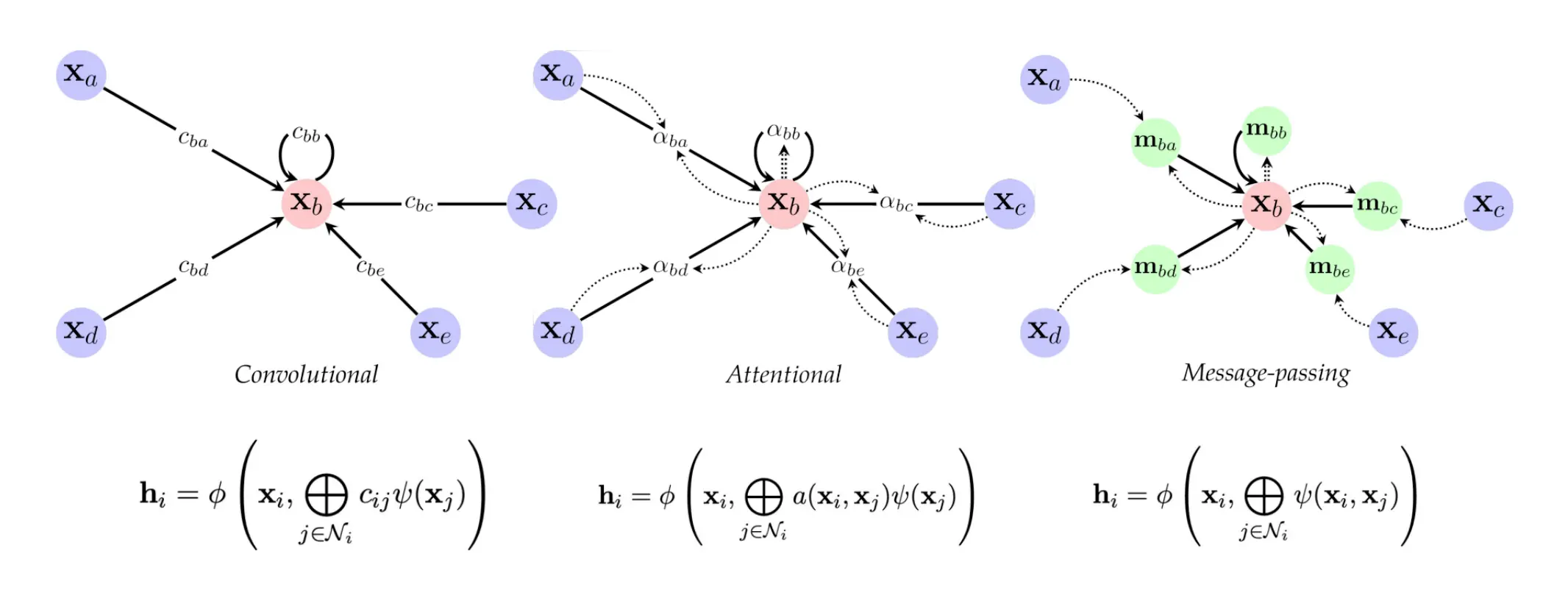消息传播大方向分类一共有3种，也就是卷积型，attention型，和消息传播型。

• 卷积式，类似于卷积运算，权重 cij​ 是基于图结构预定义的，通常与节点之间的连接强度或图的拓扑结构相关。
• 注意力式，权重动态调整。
• 消息传递式，GNN 的一个通用框架，允许灵活地定义从邻居节点 j 到目标节点 i 的消息 mij​ 的形式。

CNN其实可以看成是一种特殊的，固定邻居和顺序的GNN，而GNN是可以处理任意形状的图的。

Polling Layer

在GNN中，一般有两种池化的分类。一种就是Flat Polling（也叫Readout），也就是对全图进行一个池化，得到一个结果；另一种叫Hierarchical Polling，即对某一簇进行池化。下面就是分层池化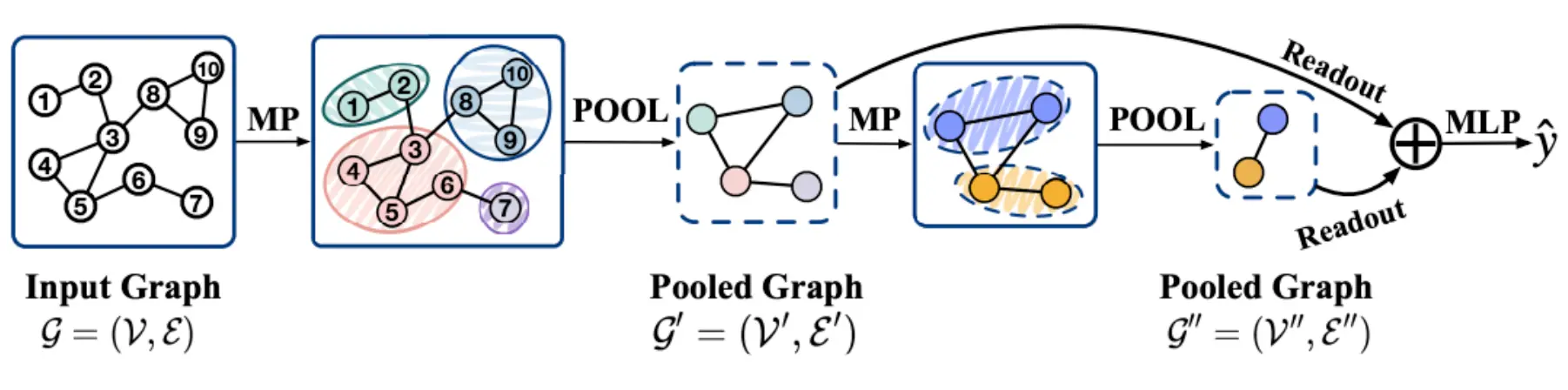： 池化通过将节点的隐藏状态聚合成为图嵌入，最终用于更高级的工作。

Permutation Equivariance and Invariance

图的节点通常没有固定的排列顺序（Canonical Ordering），即节点的编号或顺序可以随意调整，而不会改变图的拓扑结构。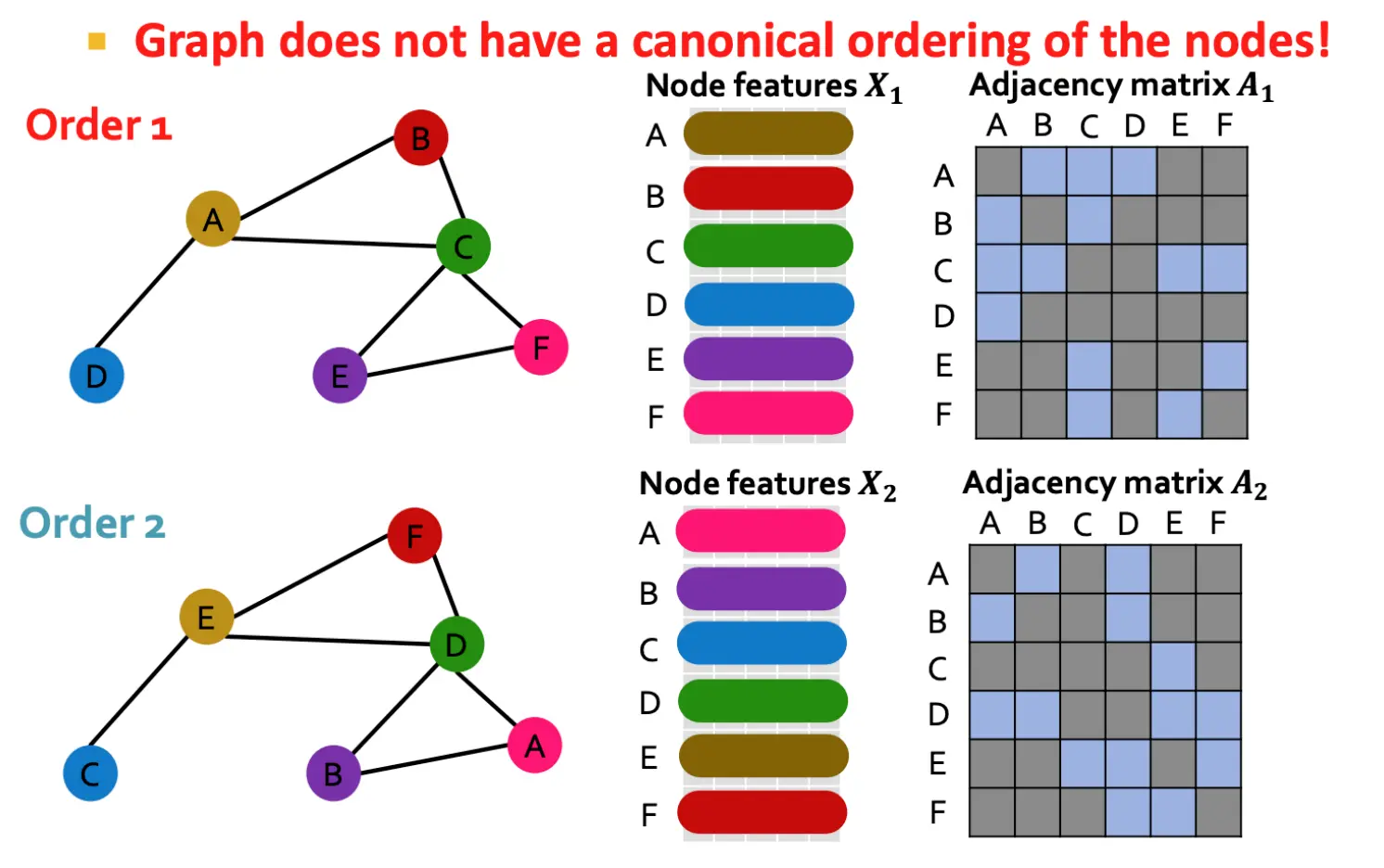

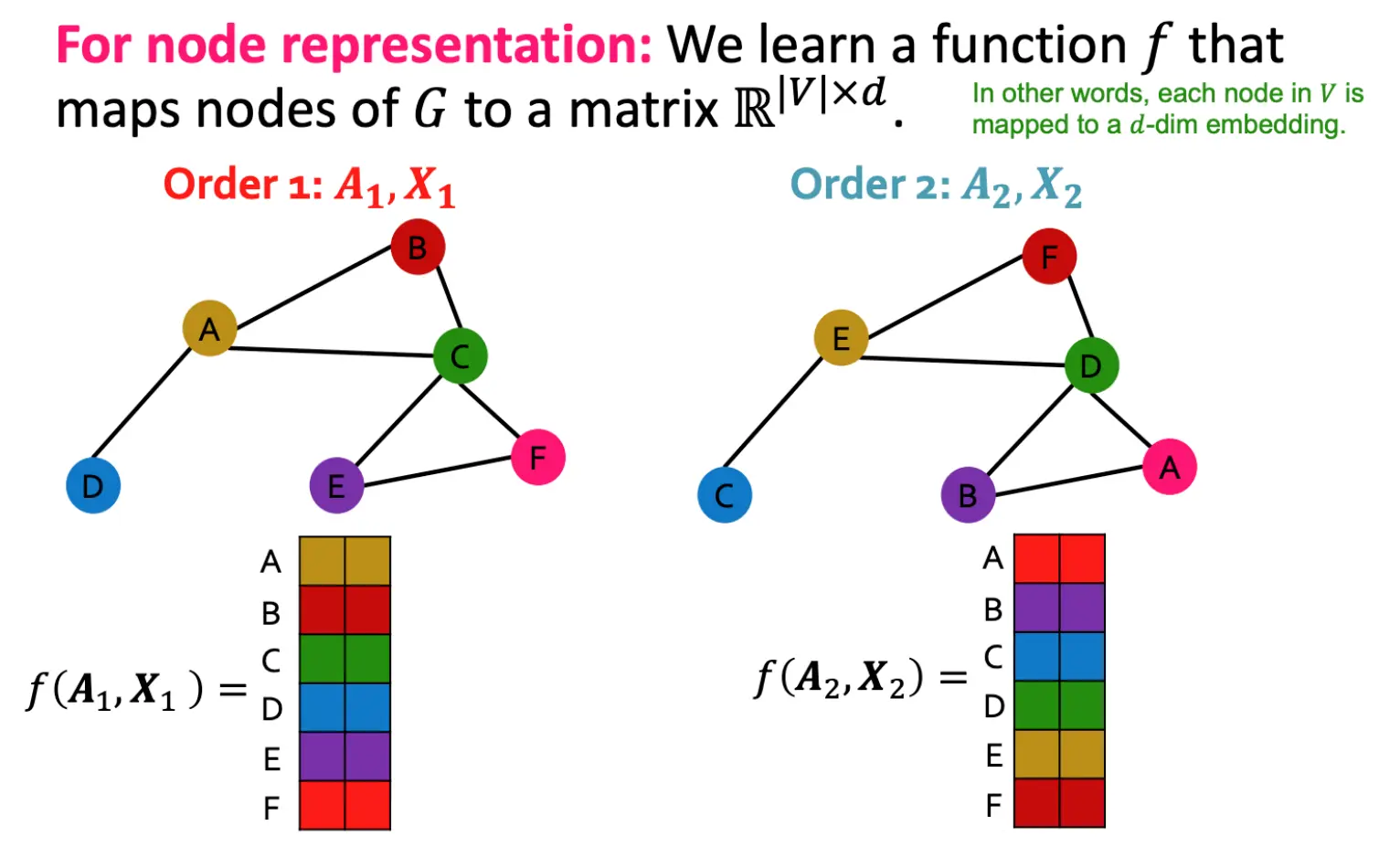
• Order 1：

  • 节点按 ( A, B, C, D, E, F ) 的顺序排列。
  • 输入邻接矩阵 ( A_1 ) 和特征矩阵 ( X_1 )。
  • 输出嵌入矩阵 ( f(A_1, X_1) )，每一行对应节点 ( A, B, C, D, E, F ) 的嵌入。

• Order 2：

  • 节点按 ( E, C, B, F, D, A ) 的顺序排列。
  • 输入邻接矩阵 ( A_2 ) 和特征矩阵 ( X_2 )。
  • 输出嵌入矩阵 ( f(A_2, X_2) )，每一行对应节点 ( E, C, B, F, D, A ) 的嵌入。

• 关键点：

  • 尽管节点的顺序不同，函数 ( f ) 的输出会根据输入顺序调整，但每个节点的嵌入值保持一致。
  • 例如，节点 ( A ) 的嵌入在 Order 1 和 Order 2 中是相同的，只是它在输出矩阵中的位置不同。

1. 仅有节点的图（集合表示）

   • 输入：节点特征矩阵 (X)。
   • 置换不变性：$$f(PX)=f(X)$$
     • 对节点特征矩阵 (X) 应用置换矩阵 (P)，函数 (f) 的输出保持不变。
   • 置换等变性：$$f(PX)=Pf(X)$$
     • 对节点特征矩阵 (X) 应用置换矩阵 (P)，函数 (f) 的输出会以相同的方式置换。

2. 包含节点和边的图

   • 输入：邻接矩阵 (A) 和节点特征矩阵 (X)。
   • 置换不变性：$$f(PA{P}^T,PX)=f(A,X)$$
     • 对邻接矩阵 (A) 和特征矩阵 (X) 应用置换矩阵 (P)，函数 (f) 的输出保持不变。
   • 置换等变性：$$f(PA{P}^T,PX)=Pf(A,X)$$
     • 对邻接矩阵 (A) 和特征矩阵 (X) 应用置换矩阵 (P)，函数 (f) 的输出会以相同的方式置换。

GNN置换等变性来源：

• 在消息传递阶段，GNN 对邻居节点的排列顺序敏感，但通过无序的聚合操作（如求和、平均等），保证节点表示的一致性。 置换不变性来源：
• 在池化阶段，GNN 聚合所有节点表示生成图表示，对节点排列顺序完全不敏感。 MLP 和 CNN 不具备处理无序数据的能力，对输入顺序敏感。

贡献者

Larry Shi

文件历史

最后编辑于 10 天前查看完整历史

67e39-update image format from gitbook style to standard markdown style

f9aec-update