VC dimension

字数

1443 字

阅读时间

6 分钟

上一次我们说到，由于Bad Event之间是有交集的，所以P(Bada or Badb or Badc)如果仅仅被替换为P(Bada) + P(Badb) + P(Badc)其实是让整个条件变松了。真实的结果应该远小于这个加和。也就是说，我们想要找到一个合理的mH来替换M

$$\mathbb{P}[|E_{\mathrm{in}}(g)-E_{\mathrm{out}}(g)|>ϵ]\le 2\cdot M\cdot \exp (-2{ϵ}^{2}N)$$

而这个合理的mH我们上次说，是H中二分点集x1..xn的最大分类方法数，而这个最大分类方法数 <= 2^N 这个mH我们叫做生长函数。

$$m_{\mathcal{H}}(N)=\underset{{\mathit{x}}_1,...,{\mathit{x}}_N\in \mathcal{X}}{max}|\mathcal{H}({\mathit{x}}_1,...,{\mathit{x}}_N)|$$

Growth Function

$$m_{\mathcal{H}}(N)=\underset{{\mathit{x}}_1,...,{\mathit{x}}_N\in \mathcal{X}}{max}|\mathcal{H}({\mathit{x}}_1,...,{\mathit{x}}_N)|$$

如何计算生长函数？

对于直线左负右正二分类

mH = N+1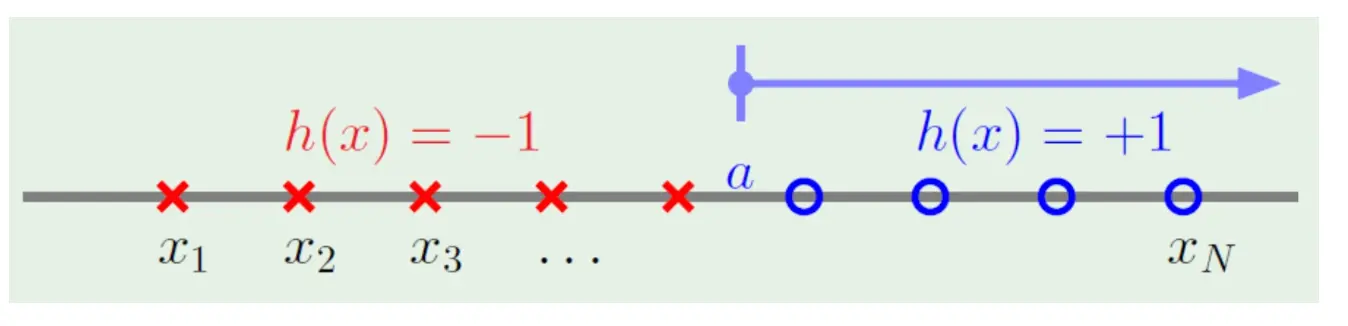

对于直线中间正两边负二分类

mH = 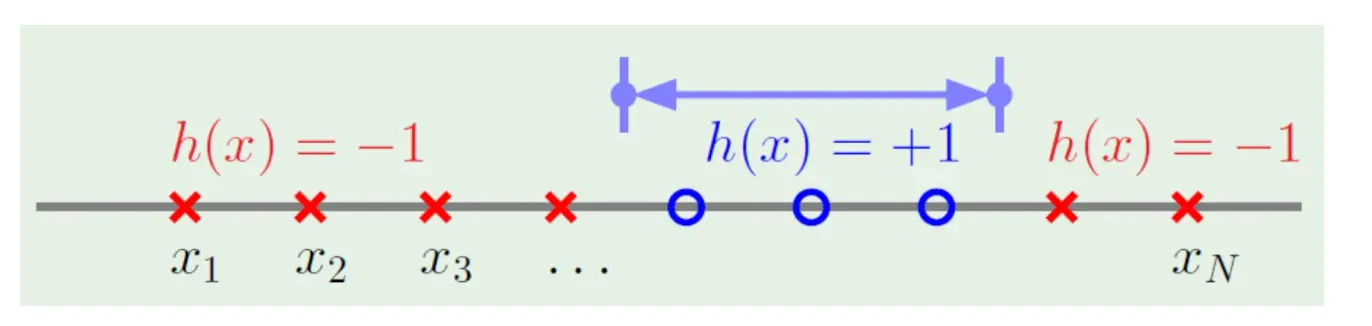$C_{N+1}^2+1$

对于2D感知机

小于2^N, 其中mH(2个点) = 4， 3个点=8 ，4个点=14，5个点=22。这里要注意的是，这里只看最大能分类，而不是在特定的点上。只要维度对得上，点在哪里都可以，只要能分类最大数量就可以。

对于凸集

mH = 2^N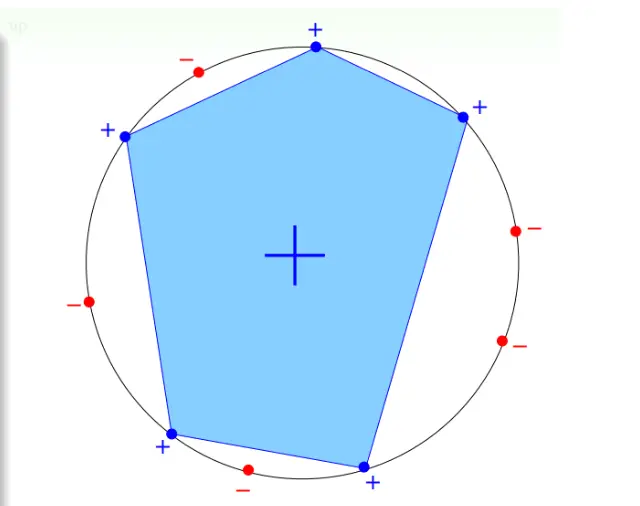

Shatter

如果一个假设集H能够对一个点集x1 .. xn产生出2^N种二分法，那么我们称H shatter 了 X 对于2D感知机，N=3就shatter，4就不shatter，对于凸集，全部shatter

VC Bound

我们原先有：

$$\mathbb{P}[\mathrm{\exists }h\in \mathcal{H}\mathrm{s}.\mathrm{t}.|E_{\mathrm{in}}(h)-E_{\mathrm{out}}(h)|>ϵ]\le 2m_H(-N)\cdot \exp (-2{ϵ}^{2}N)$$

而实际中，当N足够大的时候，有进一步的推导。这数学很复杂：

$$\mathbb{P}[\mathrm{\exists }h\in \mathcal{H}\mathrm{s}.\mathrm{t}.|E_{\mathrm{in}}(h)-E_{\mathrm{out}}(h)|>ϵ]\le 2\cdot 2m_{\mathcal{H}}(2N)\cdot \exp (-2\cdot \frac{1}{16}{ϵ}^{2}N)$$

如果展现整个从霍夫丁选g到VC Bound的过程，就是这样：

$$\begin{array}{rl}& {\mathbb{P}}_{\mathcal{D}}[|E_{\mathrm{in}}(g)-E_{\mathrm{out}}(g)|>ϵ]\\ & \le {\mathbb{P}}_{\mathcal{D}}[\mathrm{\exists }h\in \mathcal{H}\mathrm{s}.\mathrm{t}.|E_{\mathrm{in}}(h)-E_{\mathrm{out}}(h)|>ϵ]\\ & \le 4m_{\mathcal{H}}(2N)\exp (-\frac{1}{8}{ϵ}^{2}N)\end{array}$$

而进一步，如果在某一个N的时候你的H不能shatter了，那么就存在max N可以shatter，我们记这个Max N为k，则有

$$\begin{array}{rl}& {\mathbb{P}}_{\mathcal{D}}[|E_{\mathrm{in}}(g)-E_{\mathrm{out}}(g)|>ϵ]\\ & \le {\mathbb{P}}_{\mathcal{D}}[\mathrm{\exists }h\in \mathcal{H}\mathrm{s}.\mathrm{t}.|E_{\mathrm{in}}(h)-E_{\mathrm{out}}(h)|>ϵ]\\ & \le 4m_{\mathcal{H}}(2N)\exp (-\frac{1}{8}{ϵ}^{2}N)\\ & \stackrel{\mathrm{if}k\mathrm{exists}}{\le }4(2N{)}^{k-1}\exp (-\frac{1}{8}{ϵ}^{2}N)\end{array}$$

条件为：1. 有k 2. N足够大 3. Ein足够小

VC Dimension

上面我们说了k，其实他有个正式名字叫VC Dimension。也就是最大shatter N。对于生长函数和vc维，有这样的关系：

$$\begin{array}{r}{m}_{\mathcal{H}}(N)\le N^{d_{\text{VC}}}+1\end{array}$$

这也就是上面能成立的原因。 例如，一个矩形分类器的VC维是4.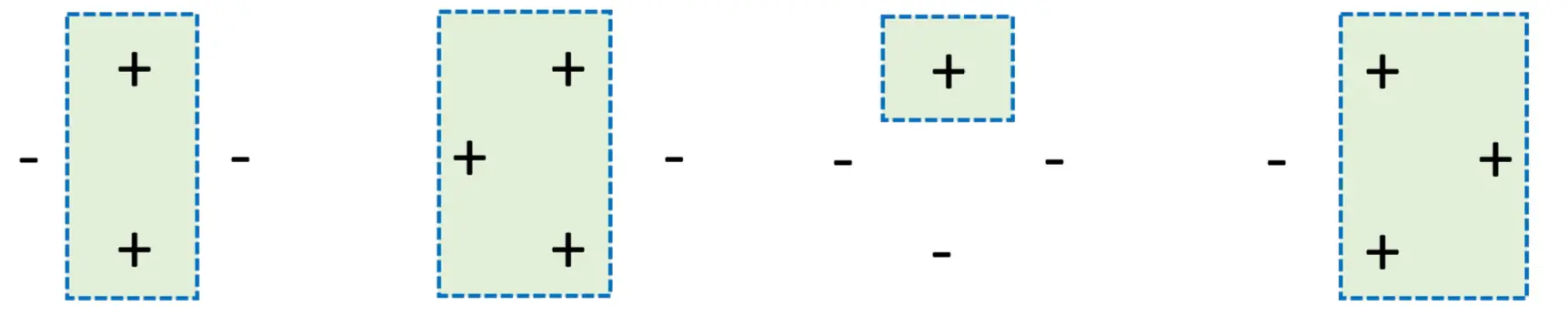

常见分类器的VC维：

• 感知机：输入空间维度+1.

$$\begin{gathered} \mathcal{X}={\mathbb{R}}^d\cup \{1\},i.e.,(x=[1,x_1,\dots ,x_d{]}^T). \\ {d}_{\mathrm{VC}}=d+1. \end{gathered}$$

• 正射线 dVC = 1
• 正间隔，dVC = 2
• 凸集，无限

现在如果我们定性看M和dVC对训练的影响，

VC Bound重述

模型复杂度

当我们用生长函数表达bound的时候，长这样：

$$E_{\mathrm{out}}(g)\le E_{\mathrm{in}}(g)+\underset{=ϵ(N,\mathcal{H},\delta )}{\underbrace{\sqrt{\frac{8}{N}\log \frac{4m_{\mathcal{H}}(2N)}{\delta }}}}$$

如果我们用VC dimension替换生长函数，那么有

$$ϵ(N,d_{\mathrm{VC}},\delta )=\sqrt{\frac{8}{N}\log \left(\frac{4((2N{)}^{d_{\mathrm{VC}}}+1)}{\delta }\right)}$$

这相当于是个惩罚项，N大了，惩罚就小，Ein和Eout就接近。dVC大了，假设集就复杂，epsilon九大，Ein和Eout就离得远。置信度越高，也就是delta越小，那么要求就越严格，惩罚项就越大。 所以VC dimension和各项的关系就是这样的：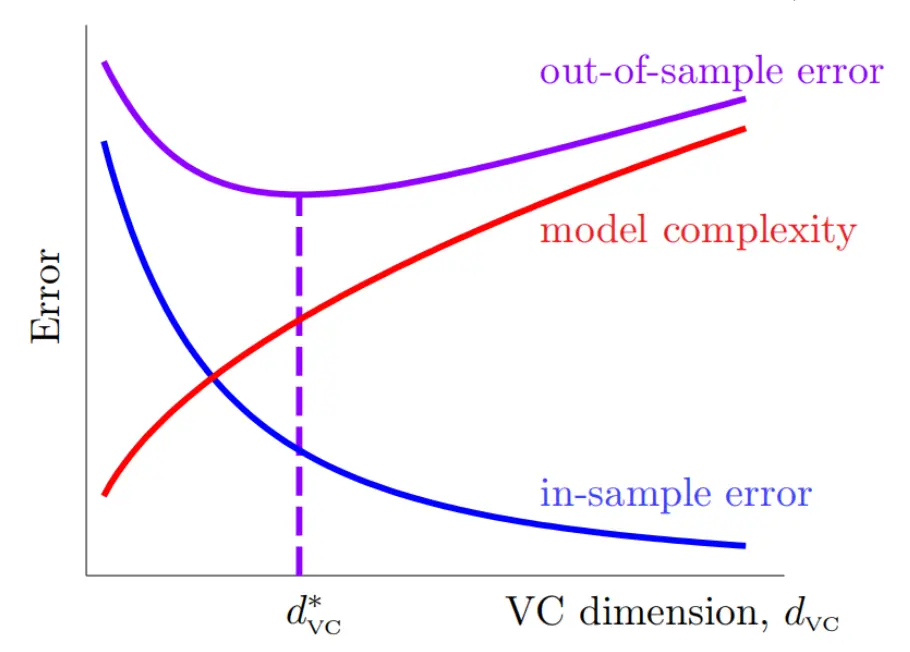

样本复杂度

如果我们希望置信度为某个1 - delta，那么我们可以强迫：

$$\sqrt{\frac{8}{N}\log \frac{4m_{\mathcal{H}}(2N)}{\delta }}\le ϵ.$$

同样，用VC维替代后，可以得出解N的bound：

$$N\ge \frac{8}{{ϵ}^2}\log \left(\frac{4(2N{)}^{d_{\mathrm{VC}}}+1}{\delta }\right).$$

这样，我们就可以预期计算一下想达到某个效果，需要的数据量了。 理论上，N需要等于10000倍的VC维才够，到那时一般N为10倍VC维的时候就够了。

Non-Linear transformation

在前面，我们已经尝试使用核技巧来将输入空间转化为特征空间，从而使得原问题具有非线性分割的能力。2 - Logistic-Regression 然而，VC维也会随着你嵌入的进行而变大。因为你可以进行很多以前没法二分的情形。对于一个Q阶的非线性嵌入 模型很容易就会出现复杂性过大的问题。 w数量的增长速度 $1+\tilde{d}=C_{Q+d}^d=O(Q^d)$ 而根据经验又有 $1+\tilde{d}\approx d_{VC}({\mathcal{H}}_{{\mathrm{\Phi }}_Q})$，所以增长很快 而VC维也是有一个上限的。$$d_{\mathrm{VC}}(\mathcal{H}_{\Phi_Q})\leq\tilde{d}+1$$ 这是因为，你的自由调整度就是d+1，所以你最多就能调整自己shatter d+1个维度的点。d+2就不行了。 简而言之：

SVM的VC维

因为SVM使用的是线性分类器，所以它的VC维受限于输入空间的维度d，具体上限是d+1。 SVM通过最大化分类间隔（margin）来选择分类超平面，这意味着选择一个“胖”的（即宽度更大的）分离超平面。 胖超平面比薄的超平面更不容易“shatter”数据点

考虑所有有宽度至少为ρ的胖超平面的假设集合，设为H_ρ。当我们将假设集限制为只包含这些胖的超平面时，可以减少能被完全分割（即shattered）的点数。具体来说，使用这些宽度至少为ρ的分离超平面所形成的假设集的VC维低于线性模型的VC维（d+1）。

对于一个瘦平面，在N=3的时候可以打散，也就是4个都满足。但是胖的只能打散2个。 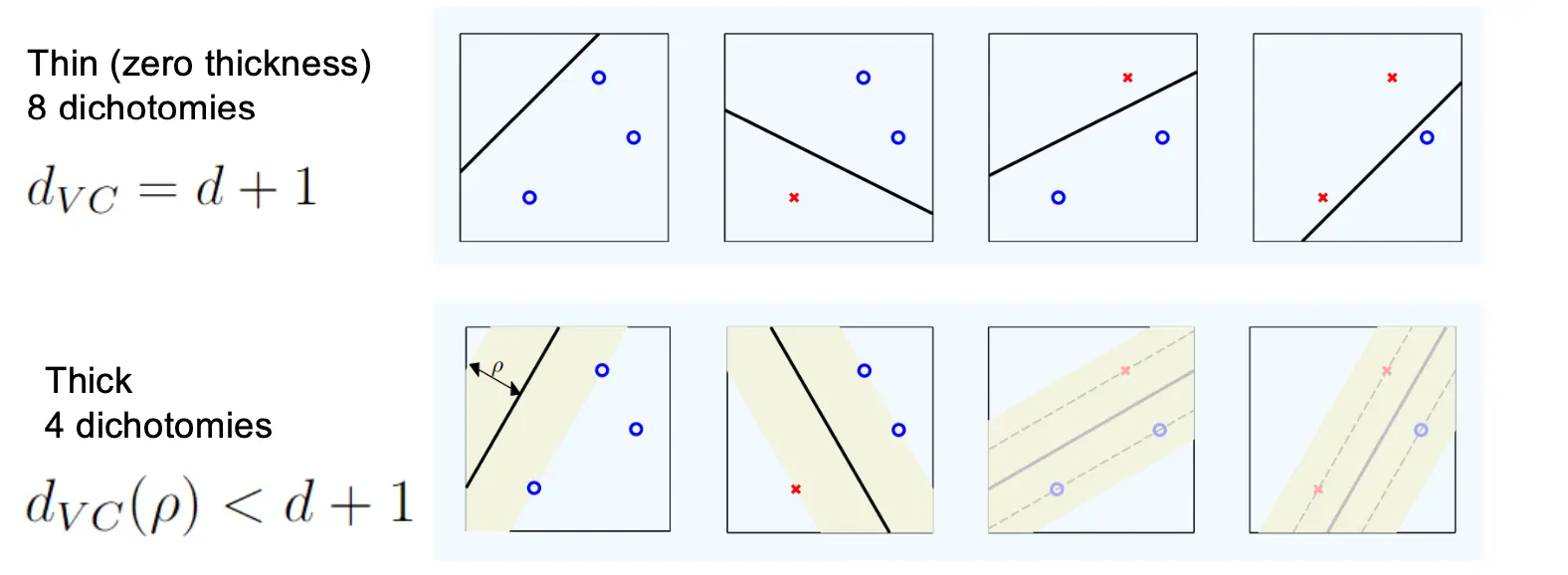具体来说，如果输入空间维半径为R的球体，而最大间隔为rou，那么有

$$d_{\mathrm{VC}}(\rho )\le \lceil R^2/{\rho }^2\rceil +1,$$

贡献者

Larry Shi

文件历史

最后编辑于 7 天前查看完整历史

6b50e-update ml

f9aec-update