Multi-Objective Optimization

字数

2021 字

阅读时间

8 分钟

Motivation问题

我们经常会遇到这样的问题：

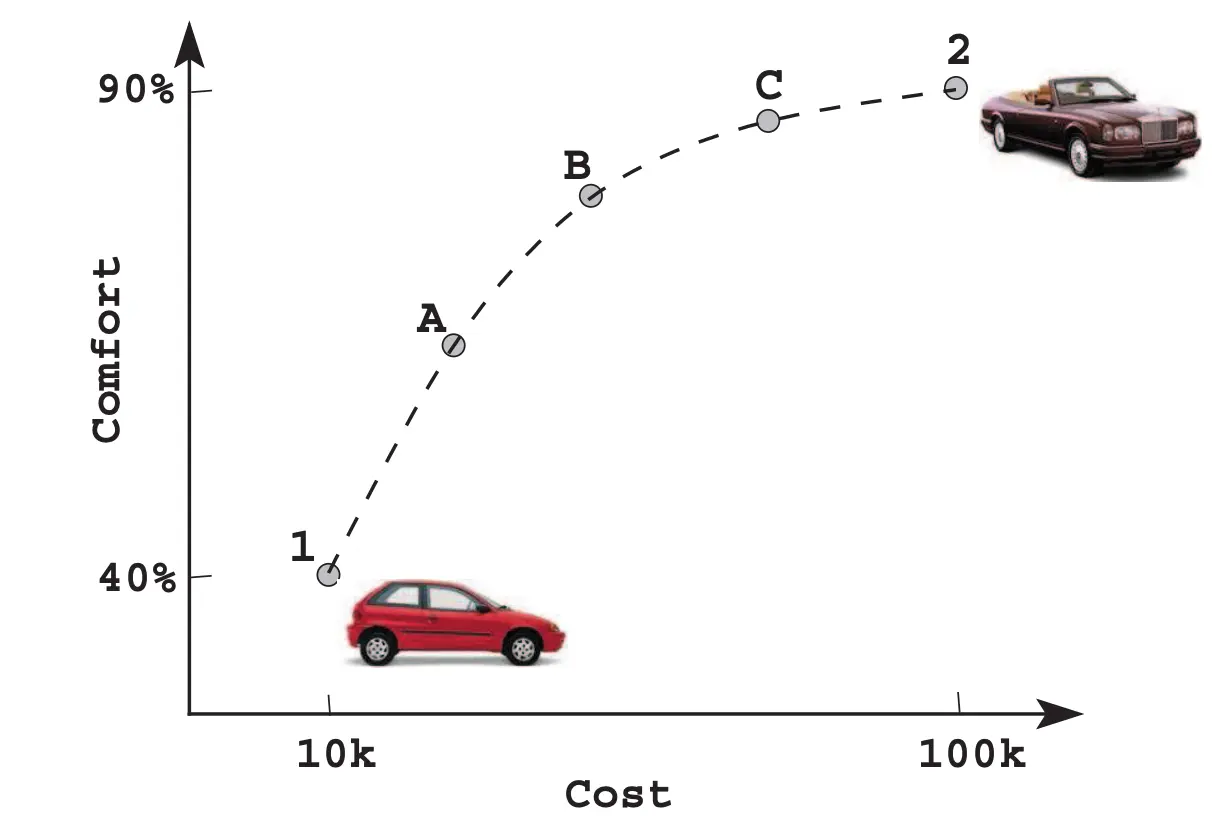
Pareto-Optimal

首先定义domination支配。 我们说，x1支配x2，当x1的所有指标都等于或优于x2，且至少有一个指标比x2好。 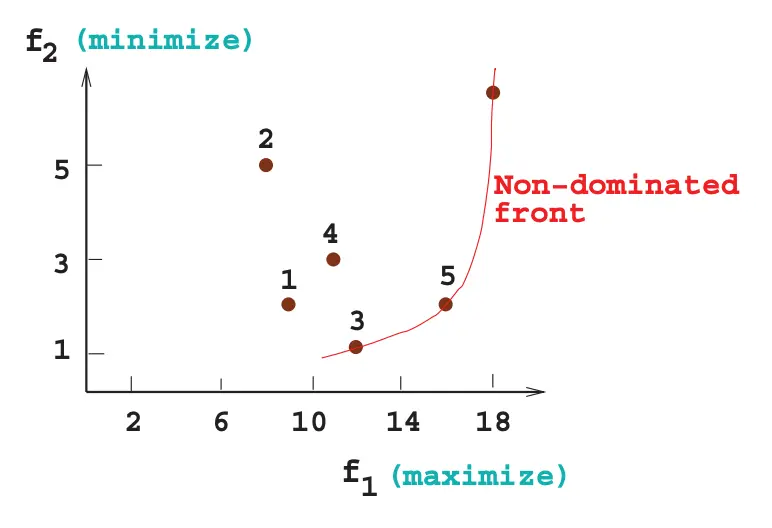在本图里面，3 5还有上面的点都是没有其他点所能支配他们的，这个子点集叫做Pareto-Optimal solutions。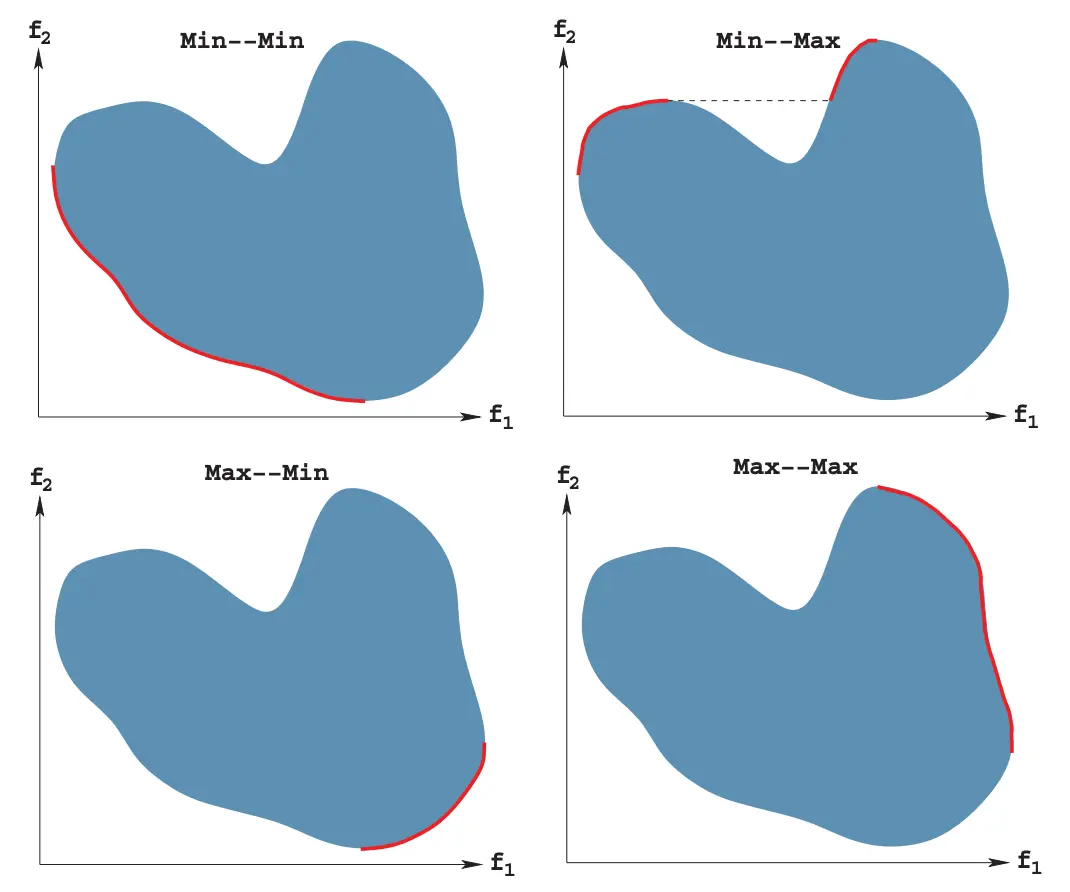

Weighted Sum Method

简单方法：权重加和，就是为每个指标都赋予一个权重，这个权重来自于专家知识。 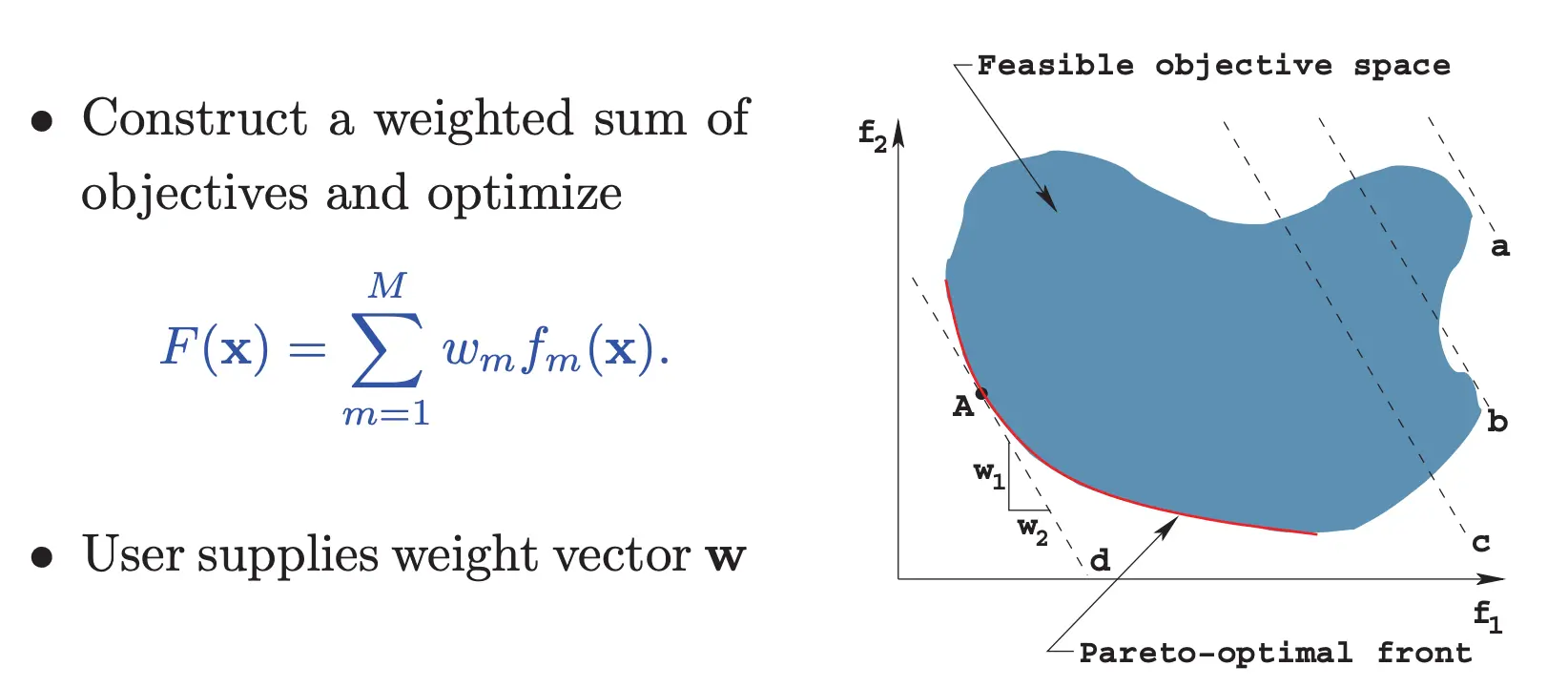然而这个方法有很多问题。 首先，你需要专家知识来知道w。 其次，由于你不断变化斜率来找到pareto前沿，斜率越大，你移动f1得到的点间隔就越大，这会导致在前沿上采样点不均匀。 最后，如果你的搜索空间不是凸的，你就得不到凹进去部分的解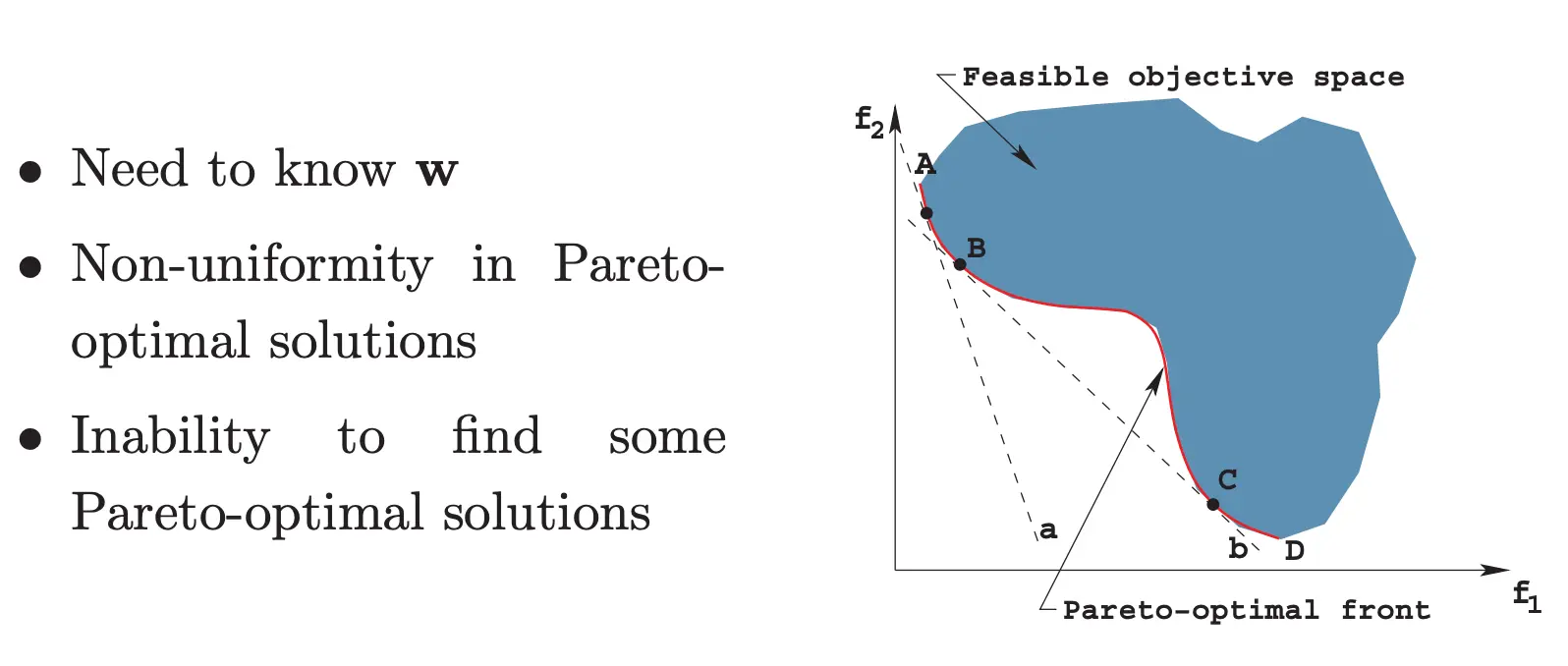

理想多目标优化的过程

理想的过程是：找到Pareto最优点集，然后再在这个点集中选择用户最想要的一个点。 而为了满足这个理想的过程，我们的优化过程就要做到两点：

1. 能够收敛到Pareto前沿
2. 在前沿上点的采样要尽量均匀 一个确定性的识别Pareto的方法：

MOEA

要使用Elite Preservation

如果不进行精英保护，那么可能很难快速收敛。所以MOEA也要进行精英保护。 我们要进行3个任务

• Elite preservation
  • 维护非支配解的存档
• Progress towards the Pareto-optimal front
  • 更倾向于非支配解
• Maintain diversity among solutions
  • 在archive中进行聚类、定位或基于网格的竞争

NSGA-II (Non-dominated Sorting Genetic Algorithm)

我们要介绍NSGA-II算法

Non-dominated Sorting

首先就是Non-dominated Sorting，这个算法负责计算出多个非支配层P1，P2，....，Pn，P1就是Pareto前沿，P2仅被P1支配，以此类推 对于所有点i，都为其初始化一个Si和ni，Si存储着被i支配的点，ni存储着支配i的点数量。 然后就是一层一层剥洋葱，得到每一个P。 如果有M个指标（objective），N个个体，那么这个算法的时间复杂度为O(MN2)。其中第一个循环的时间复杂度为O(MN2)，因为每个个体要和自己种群比，就是N2，而有M个指标，所以比M次。第二个循环的时间复杂度是O(N2).

我们得到每个Pi之后，对于最后的种群，我们肯定希望从P0开始往进加，一直加到种群数量达到，但是其实很少能够正好达到种群数量，大多时候加入最后一个Pi的时候数量会超，那我们怎么选择哪些Pi中的解保留呢？根据Crowding Distance。

Crowding Distance

我们说过我们希望得到均匀分布的解。这个Metric衡量了一个解周围解的拥挤度。可想而知，我们从拥挤度低的加到高的，那么种群的解就会比较分散。 这里的输入是一个解集F，里面每个元素fi都有M个f，就是M个目标函数。 首先，对于所有解i的拥挤度都设为0，接着对于每个objective m，按照m的大小为fi排序，i就被打乱了。设最优解和最劣解的拥挤距离设为无穷，对于中间的解，按照公式计算密度。在所有objecttive上的拥挤度会被压缩到d一个一维数字里。

NSGA-II

这就比较简单了 先把父子种群合并，然后不断加入P小的前沿，加不动了就按照拥挤度往进加。 用拥挤度的方法过程类似于这样：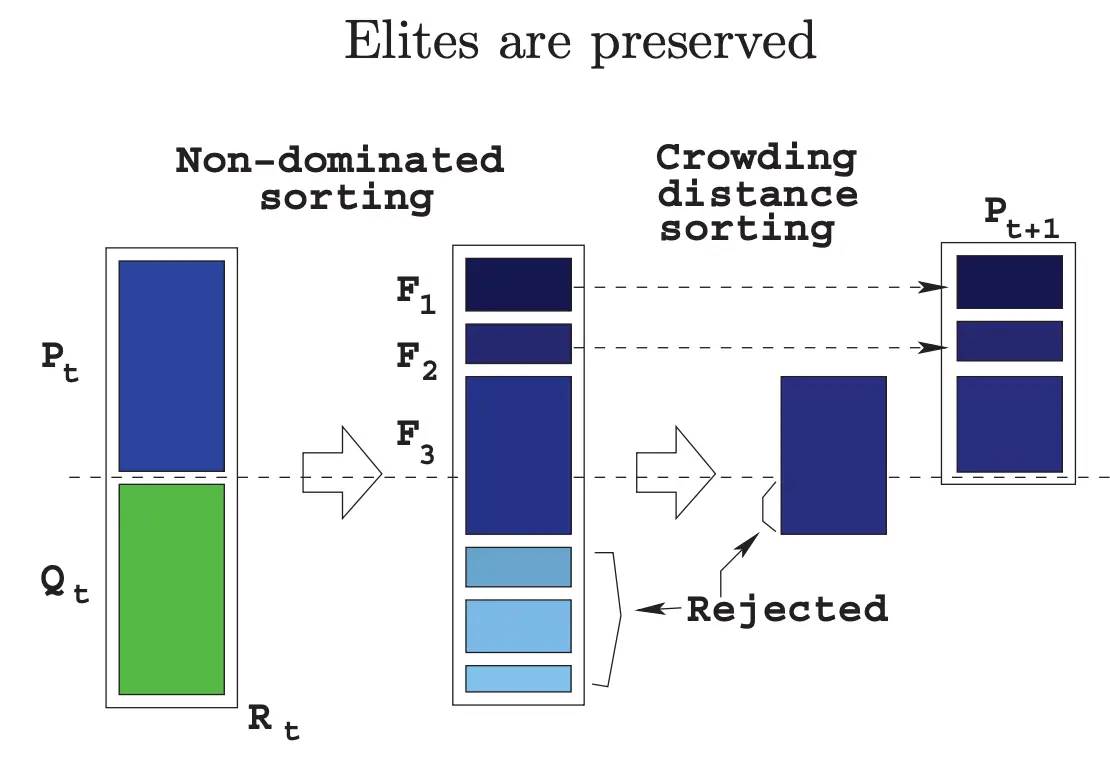

Strength Pareto EA (SPEA)

这个没怎么讲，但是说一下 强化 Pareto 进化算法。这个算法通过在外部让所有非支配解存下来来保护非支配解

• SPEA 维护一个外部存档（external archive），用来存储当前找到的所有非支配解（Pareto optimal solutions）。 对于外部的精英存档，计算每一个精英支配种群中解的数量Si 对于种群中的解，其fitness为外部每一个支配它的解的Si的和。可想而知这个fitness越小越好。 然后进行选择和重组，这主要依靠对当前种群和外部精英库进行锦标赛选择。 最后如果外部精英库的数量超过了上限就会用一些聚类方法来舍弃一些相似的解。

Pareto Archived ES (PAES 1+1)

“(1+1)-ES” 表示每次只有 1 个父代（pt​）和 1 个子代（ct​）；通过变异操作产生子代，然后根据某些准则决定下一代用谁。 假设时刻t有一个父代pt，一个子代ct和（由pt变异产生）一个外部档案At，算法通过比较ct和At来决定下一代的pt+1以及At+1 具体来说：

• 如果ct被At中的任何解支配，那么父代pt+1 = pt，At不变
• 如果ct支配了At中的某些解，那么把被支配的解从At里面删了，把ct加进去，pt+1 = ct
• 如果都不成立，但还At还没满，那么ct进入At，pt+1 = winner(ct, pt), winner的判定通常基于在档案中所处的拥挤度或多样性指标
• 若档案已满，ct 所落区域并不是最拥挤的区域，就把最拥挤区域里的某个解剔除，用 ct​ 替换掉，让档案更均匀；父代更新则依据拥挤度原则决定谁留下。

约束处理

$$F_m=f_m+R_m\mathrm{\Omega }(\overrightarrow{g}).$$

Rm是一个因子矩阵，omega是violation

显式地处理不可行解的策略：

• Jimenez’s approach
  • 在算法流程中增设一些明确的筛选或修复
  • 对不可行解进行一定的“可行化修补”，或者在种群选择阶段强制淘汰一部分违反较严重的解，以此减少不可行解占比。
  • “显式地”把不可行解当成一个单独的集合来管理或操作。
• Ray–Tang–Seow’s approach
  • 在算法某个阶段单独处理不可行解，而不是一刀切地全部丢弃。
  • 也有的实现会对不可行解设定不同等级的惩罚或优先修补策略，还可能结合局部搜索等手段试图把不可行解拉回到可行域附近。

修改了对“支配”的定义

• Fonseca and Fleming’s approach
  • 在原始“解 A 支配解 B”的定义上，增加对约束可行性的判断，通常会规定：
    • 任何可行解都优于（支配）任何不可行解；
    • 对于两个都不可行的解，也可以比较它们的违约程度，违约少的“更好”；
    • 对两个都可行的解，再进行传统的多目标支配比较。
    • 形成一个“分层”的支配关系，引导算法优先倾向可行解，并在不可行解之间也有细致的比较。
• Deb et al.’s approach（NSGA-II）
  • 如果一个解是可行的而另一个是不可行的，则可行解胜；
  • 如果两者都可行，则使用常规的 Pareto dominance 比较；
  • 如果两者都不可行，则比较它们的约束违反总量，较小者胜。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update