Week 2 Optimization & Local Search

字数

1472 字

阅读时间

6 分钟

Traveling Salesman Problem

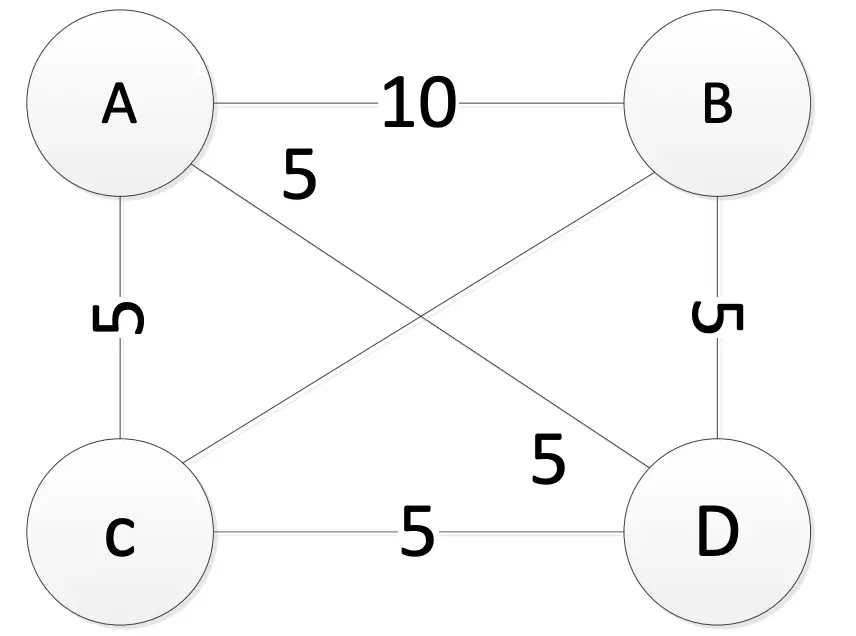TSP问题是NP难问题，所以线形规划无法在多项式时间里解决。 很多问题都是TSP变种，比如，打印PSB电路板，Scheduling，载具路径规划 TSP概念上简单但计算上困难：组合优化算法开发与评估的最佳基准

Optimization

• 可以利用数学工具解决，比如线性规划
• 可以利用搜索或枚举解决
  • Brute Force
  • 分支限界
  • 启发式算法
    • 随机算法
    • Local Search，比如贪心搜索

Random Search

根据Week 1 Intro & Randomised Algorithms中写到的：

随机算法有两类：

1. 利用随机数来找到问题的解决方案 -> Monte Carlo & Les Vegas
2. 利用随机数来改进问题的解决方案

如何用第一种来解决TSP？ Las Vegas: 不断尝试随机排列城市的访问顺序，直到找到最优解（可能需要很长时间）。 Monte Carlo: 随机生成多个可能的路径，并选择最短的一个，即便它未必是最优解。

如何在一开始生成初始解？ 采用随机排列城市顺序的方法构造解，然后利用模拟退火或者遗传算法来优化解。 结果：随机搜索算法（如 Monte Carlo 或 Las Vegas）得到的结果很差，因为：

• 搜索空间巨大，随机生成的路径几乎不可能接近最优解。
• TSP 需要全局优化，但随机搜索不会主动收敛到更优的解。

Local Search

基本思路是，从一个猜测的解开始，不断进行incrementally improve（增量式改进），得到一个较好的解 什么是增量式改进呢？就是通过局部变化（local changes）优化，不断尝试移动到临近解（neighbor solution） 什么是临近解呢？看如何定义。在TSP中，一个解的领居可以是交换两个城市顺序之后的路径；在排课问题中，一个解的邻居可以是调整某一门课后整体的课表。

缺点：容易陷入local minimum. 注：终止条件可以是达到最大迭代次数或在若干次迭代后无改进。

Hill Climbing —— 最简单的局部搜索

它只关注当前状态，不记得之前的搜索路径。

• 从一个任意初始解开始
• 做一次修改，得到邻近解。注意，如果是simple hill climbing, 那么只要好就爬。如果是steepest hill climbing, 那么要把所有immediate neighbor solutions都比一遍再选最陡的
• immediate neighbor solutions指的是与当前解最相似的解。

这里展示Simple Hill Climbing的伪代码：

那么如何得到这个immediate neighbor solution呢？可以通过2-Opt交换来得到。

2-Opt Algorithm

2-Opt algorithm是一种得到immediate neighbor solution的方法，是hill climbing algorithm的一个环节。 其思想是，在城市中选择两个nodes，交换其位置，然后将夹在两个nodes中间的nodes反序，然后再连接。

注意到，2-Opt算法是可以去交叉的。这个就像是扭了一圈，很好理解。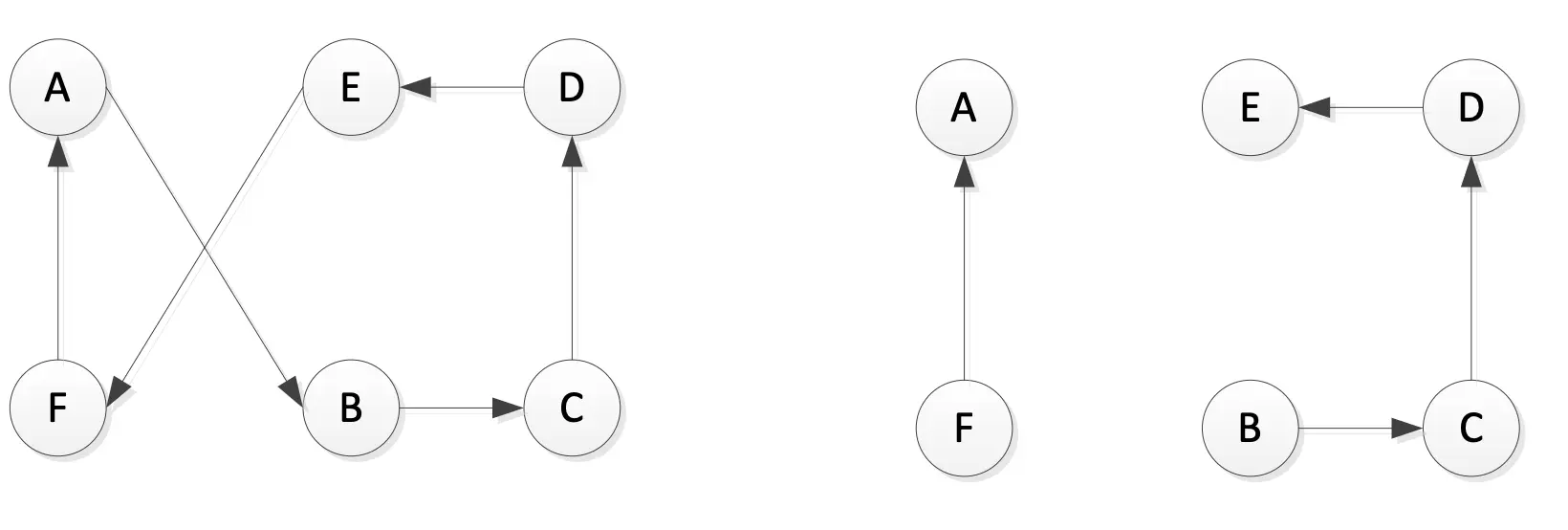

小结

随机搜索，擅长探索，比如探索大范围空间，但在解附近的小搜索空间内搜索效果差 局部走索，擅长至少找到一个局部最优，但是很难跳出从而得到全局最优。

Stochastic Local Search

也是一种Local Search。不在里面写只是因为标题级数不够用了。 其目标是通过引入随机性，来帮助算法逃出局部最优，找到全局最优。

有两种思路：

• Random Restart
  • 当陷入局部最优时，重新开始选择一个最初的随机解，重新搜索。
  • 适用于局部最优的数量较少（大多数初始解可以收敛到全局最优），并且重新开始成本不算太大的搜索
• Random non-improving step：引入随机非改进步
  • 在局部搜索中，偶尔允许算法移动到一个比现在差的邻居解。
  • 例子：模拟退火 Simulated Annealing
    • 以一定概率接受更差的解，随着搜索进行，接受更差解的概率逐渐降低。

Simulated Annealing 模拟退火

其想法来源于真实的金属退火过程。 如何让金属变的更坚硬？先加热，然后再让其慢慢降温。这样钢结构会逐渐找到一个稳定的低能态。 在高能的时候，允许金属有更多的内部动作，但温度低了之后，内部动作就少了。

其中，temperature函数一般是一个超参数。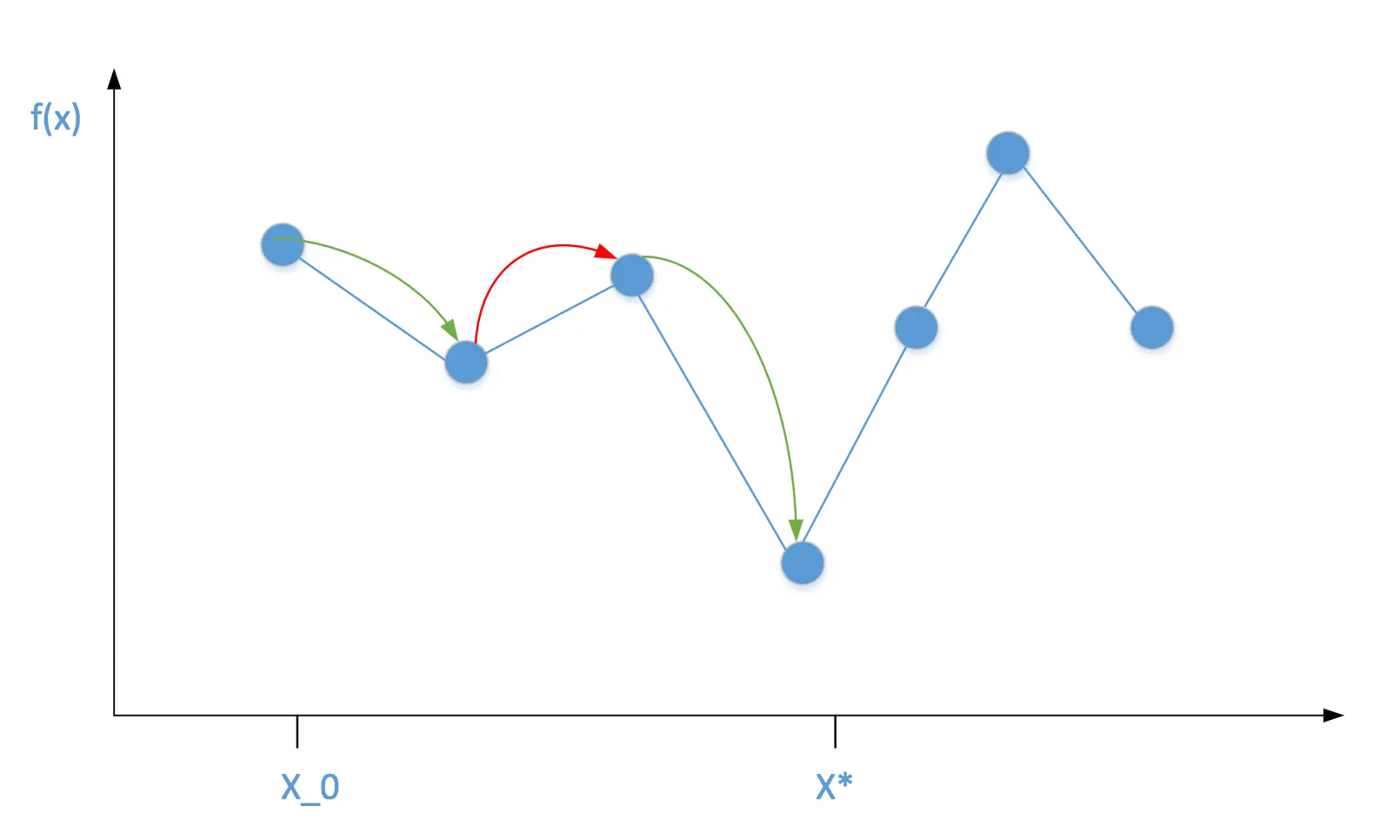

Extra: Tabu Search 禁忌搜索

在TSP（旅行商问题） 中，禁忌搜索通常使用2-opt 交换来生成邻域：

1. 初始路径：选择一个随机的城市访问顺序。
2. 邻域搜索：在路径中选取两个城市并交换它们（2-opt）。
3. 禁忌表：如果一个交换最近已经执行过（例如交换 A↔B），则该交换被标记为禁忌，防止短期内重复选择。
4. 解禁规则：如果当前解比历史最优解更优，则无视禁忌状态，接受该解。
5. 重复步骤 2-4，直到满足终止条件。

贡献者

Larry Shi

文件历史

最后编辑于 22 天前查看完整历史

f9aec-update